detrend

Subtract offset or trend from time-domain signals contained in iddata objects

Syntax

data_d = detrend(data)

data_d = detrend(data,Type)

[data_d,T_r] = detrend(___)

data_d = detrend(data,1,brkpt)

Description

detrend subtracts offsets or linear trends from time-domain input-output data represented in iddata objects. detrend either computes the trend data to subtract, or subtracts the trend that you specify.

For a more general detrending function that does not require iddata objects, see detrend.

data_d = detrend(data) computes and subtracts the mean value from each time-domain signal in data. The iddata objects data_d and data each contain input and output data originating from SISO, MIMO, or multiexperiment datasets.

data_d = detrend(data,Type) subtracts the trend you specify in Type. You can specify a mean-value, linear, or custom trend.

[data_d,T_r] = detrend(___) also returns the subtracted trend as a TrendInfo object T_r. You can obtain T_r with any of the input-argument combinations in previous syntaxes.

data_d = detrend(data,1,brkpt) computes and subtracts the piecewise-linear trends for data with segmented trends, using the breakpoints that you define with brkpt.

The second argument, which corresponds to Type, must be 1.

With this syntax, you cannot retrieve the resulting piecewise-linear trend information as an output.

Examples

Remove Biases from Signals

Remove biases from steady-state signals in an iddata object by using detrend to compute and subtract the mean values of the input and output.

Load the input and output time series data y2 and u2. Construct the iddata object data2, using the data and a sample time of 0.08 seconds.

load dryer2 y2 u2
data2 = iddata(y2,u2,0.08);

Use detrend to both compute the mean values and subtract them from input and output signals. Use the input argument Tr to store the computed trend information. Plot the original data and detrended data together.

[data2_d,Tr] = detrend(data2);
plot(data2,data2_d)
legend('Original Data','Detrended Data')

The detrended data has shifted by about 5 units. Inspect Tr to obtain the precise mean values that detrend computed and subtracted. These values are returned in the InputOffset and OutputOffset properties.

Tr

Trend specifications for data "data2" with 1 input(s), 1 output(s), 1 experiment(s):
        DataName: 'data2'
     InputOffset: 5.0000
    OutputOffset: 4.8901
      InputSlope: 0
     OutputSlope: 0

The mean of the original input is higher than the mean of the original output.

Remove Linear Trend from a Signal

Remove the linear trend from a signal in an iddata object, and overlay the trendline on a before-and-after data plot.

Load and plot signal data from the file lintrend2. For this example, only output data is provided in iddata object dataL.

load lintrend2 dataL
plot(dataL,'b')

The plot shows a clear linear trend in the data. Use detrend linear option (Type = 1) to subtract the trend from the data. detrend fits the data and determines the linear trend to subtract. Include the TrendInfo object Tr as an output argument so you can see what detrend subtracts.

[dataL_d,Tr] = detrend(dataL,1);

Plot the detrended data against the original data.

hold on
plot(dataL_d,'g')
legend('Original','Detrended','Location','northwest')

The linear trend has been removed. Inspect Tr to get more information about the removed trend.

Tr

Trend specifications for data "dataL" with 0 input(s), 1 output(s), 1 experiment(s):
        DataName: 'dataL'
     InputOffset: [1x0 double]
    OutputOffset: 0.8888
      InputSlope: [1x0 double]
     OutputSlope: 19.3830

The OutputOffset and the OutputSlope properties provide the parameters of the line that detrend removed. You can reconstruct this line, and then overlay it on the before-and-after data plot. The SamplingInstants property of DataL provides the timepoints associated with the data.

m = Tr.OutputSlope

m = 
19.3830

b = Tr.OutputOffset

b = 
0.8888

t = dataL.SamplingInstants;
TrLn = m*t+b;
plot(t,TrLn,'r')
legend('Original','Detrended','Trendline','Location','northwest')

Remove Specified Offsets from Signals

Remove known offsets from an input-output signal pair contained in an iddata object.

Detrend can compute and subtract the mean values for input and output signals, resulting in zero-mean detrended signals. However, if you already know you have specific data offsets beforehand, you can have detrend subtract these from your signals instead. Specifying the offsets also allows you to retain a non-zero operating point in the detrend result.

Load SISO data containing vectors u2 and y2. For this example, suppose that you know both signals have an offset of 4 from the expected operating point of 1. Combine these vectors into an iddata object, using a sample time of 0.08 seconds, and plot it.

load dryer2 u2 y2
data = iddata(y2,u2,0.08);
plot(data)

The known offset of 4 (from operating point 1) is visible in the plots. You can construct a TrendInfo object to capture this offset, using the function getTrend.

Create the TrendInfo object, and then set its offset properties.

T = getTrend(data);
T.InputOffset = 4;
T.OutputOffset = 4

Trend specifications for data "data" with 1 input(s), 1 output(s), 1 experiment(s):
        DataName: 'data'
     InputOffset: 4
    OutputOffset: 4
      InputSlope: 0
     OutputSlope: 0

Use detrend to subtract the offset from the data. Plot it alongside the original data.

data_d = detrend(data,T);
hold on
plot(data_d)
legend('Original','Detrended')

The offset of 4 has been removed.

Remove Segmented Linear Trends from Signals by Using Breakpoints

Detrend data with segmented piecewise-linear trends by specifying breakpoints to delimit the segments.

Most of the detrend syntaxes assume and compute a single trend for each of the signals. However, in some cases there are discontinuities in the linear trends, caused by test configuration changes, environmental conditions, or other influences. When the signal displays such segmentation, you can have detrend operate on the test segments independently. To do so, specify breakpoints in the brkpt input argument. These are the indices to the timepoints in the signal at which linear trends change slope.

You may know these breakpoints up front, based on changes that you know occurred during data collection. Alternatively, you may need to approximate them by inspecting the data itself.

Load the data, inspect its structure and contents, and plot it. This data consists of output data only in the iddata object dataLb2.

load brkTrend dataLb2
dataLb2

dataLb2 =

Time domain data set with 512 samples.
Sample time: 0.00390625 seconds        
                                       
Outputs      Unit (if specified)       
   y1                                  
                                       

plot(dataLb2)

For this example, the data has known breakpoints at indices [100 300]. Applying the sample time (property Ts), these breakpoints correspond to the actual timepoints as follows:

brkpt=[100 300];
brkpt_time = brkpt*dataLb2.Ts

brkpt_time = 1×2

    0.3906    1.1719

Detrend the data using brkpt.

dataLb2_d = detrend(dataLb2,1,brkpt);

Plot the original and detrended data.

plot(dataLb2,dataLb2_d)
legend('Original Data','Detrended Data')

The linear trend segments have been removed.

Detrend Multiexperiment Signals Using Multiple-Breakpoint Sets

Apply a unique set of breakpoints to each experiment when you detrend a Multiexperiment dataset.

Experiments within a multiexperiment dataset may contain unique linear trending discontinuities. You can apply a unique set of breakpoints to each experiment by expressing them in a cell array.

Load the data, which consists of:

• datmult, a multiexperiment iddata object containing three experiments (output only)

• bpn vectors, which provide known breakpoints for each experiment in the form of indices to timepoints

load multiexpdt datmult bp1 bp2 bp3
datmult

datmult =
Time domain data set containing 3 experiments.

Experiment   Samples      Sample Time          
   exp1         250            1               
   exp2         320            1               
   exp3         350            1               
                                               
Outputs      Unit (if specified)               
   y1                                          
                                               

bp1,bp2,bp3

bp1 = 1×2

    50   200

bp2 = 
100

bp3 =

     []

Plot the data. There are significant differences among the streams, and they drift at different rates from zero mean.

plot(datmult)
legend

For this set of experiments, it is known that there is unique trending for each run and unique discontinuities indicated by the bp vectors.

detrend can incorporate these unique characteristics if the bp information is provided as a cell array.

Construct the cell array.

bpcell = {bp1;bp2;bp3}

bpcell=3×1 cell array
    {[  50 200]}
    {[     100]}
    {0x0 double}

Apply detrend and plot the result, using the same scale as the original plot.

datmult_d = detrend(datmult,1,bpcell);
figure
plot(datmult_d)
axis([0,inf,-15,30])
legend

The experimental data are now better aligned, and do not drift significantly away from zero mean.

Detrend Input and Output Signals Separately

Apply different trend types to the input and output signals contained in an iddata object.

Detrend assumes that the same type of trend applies to both input and output signals. In some cases, there may be a trend type that is present in only one signal. You can perform detrend individually on each signal by extracting the signals into separate iddata objects. Apply detrend to each object using its individual signal trend type. Then reassemble the results back into a single detrended iddata object.

Load, examine, and plot the data in iodatab.

load septrend iodatab;
iodatab

iodatab =

Time domain data set with 1000 samples.
Sample time: 0.08 seconds               
                                        
Outputs      Unit (if specified)        
   y1                                   
                                        
Inputs       Unit (if specified)        
   u1                                   
                                        

plot(iodatab)
hold on

Both input and output plots show a bias. However, the output plot also shows an inverted V-shape trend that is not present in the input data.

Separate the input data and the output data into separate objects for detrending, using the iddata general data-selection form (see Representing Time- and Frequency-Domain Data Using iddata Objects):

data(samples,outputchannels,inputchannels)

idatab = iodatab(:,[],:);
odatab = iodatab(:,:,[]);

Remove the bias from the input data, using detrend to calculate and subtract the mean.

idatab_d = detrend(idatab,0);

Remove the bias and the inverted-V trend from the output data, using the midpoint index 500 as a breakpoint.

odatab_d = detrend(odatab,1,500);

Combine the detrended input and output data into a single iddata object.

iodatab_d = [odatab_d,idatab_d];

Overlay the detrended data on the original data.

plot(iodatab_d)
legend('original','detrended')

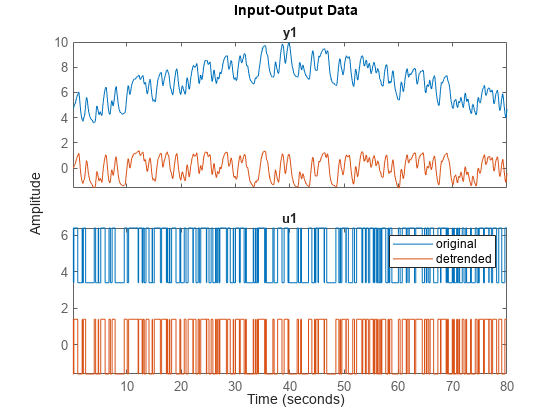
The input and output data now contain neither bias nor V-shape trend.

Input Arguments

data — Time-domain input-output data

iddata object

Time-domain input-output data, specified as an iddata object containing one or more sets of time-domain signals. The iddata object can contain SISO, MIMO, or multiexperiment data. The signal sets can contain either input and output data, or output data only.

Type — Trend type to be subtracted

0 (default) | 1 | TrendInfo object

Trend type to be subtracted, specified as one of:

• 0 — Compute and subtract the mean value

• 1 — Compute and subtract the linear trend (least-squares fit)

• TrendInfo object — subtract the trend you specify in the TrendInfo object. Use getTrend to create a TrendInfo object. For an example, see Remove Specified Offsets from Signals.

brkpt — Timepoint locations of trending discontinuities

integer row vector | cell array of integer vectors

Timepoint locations of trending discontinuities (breakpoints), specified as:

• An integer row vector — For single-experiment SISO and MIMO datasets. Doing so applies a single set of breakpoints to all input and output signals. For an example, see Remove Segmented Linear Trends from Signals by Using Breakpoints.

• A cell array containing individually-sized integer row vectors — For multiple-experiment datasets. Doing so applies a unique set of breakpoints to the output and input signals for each experiment. For an example, see Detrend Multiexperiment Signals Using Multiple-Breakpoint Sets.

Output Arguments

data_d — Detrended signals

iddata object

Detrended signals, returned as an iddata object. Dimensions of the contents are the same as dimensions of the contents of data.

T_r — Subtracted trend data

TrendInfo object

Trend data subtracted from data to produce data_d, returned as a TrendInfo object.

When you use brkpt to specify multiple trends, you cannot retrieve the computed trend data.

Version History

Introduced before R2006a