cart2pol

Transform Cartesian coordinates to polar or cylindrical

Syntax

[theta,rho] = cart2pol(x,y)

[theta,rho,z] = cart2pol(x,y,z)

Description

[theta,rho] = cart2pol(x,y) transforms corresponding elements of the two-dimensional Cartesian coordinate arrays x and y into polar coordinates theta and rho.

[theta,rho,z] = cart2pol(x,y,z) transforms three-dimensional Cartesian coordinate arrays x, y, and z into cylindrical coordinates theta, rho, and z.

Examples

Cartesian to Polar Coordinates

Convert the Cartesian coordinates defined by corresponding entries in matrices x and y to polar coordinates theta and rho.

x = [5 3.5355 0 -10]

x = 1×4

    5.0000    3.5355         0  -10.0000

y = [0 3.5355 10 0]

y = 1×4

         0    3.5355   10.0000         0

[theta,rho] = cart2pol(x,y)

theta = 1×4

         0    0.7854    1.5708    3.1416

rho = 1×4

    5.0000    5.0000   10.0000   10.0000

Cartesian to Cylindrical Coordinates

Convert the three-dimensional Cartesian coordinates defined by corresponding entries in the matrices x, y, and z to cylindrical coordinates theta, rho, and z.

x = [1 2.1213 0 -5]'

x = 4×1

    1.0000
    2.1213
         0
   -5.0000

y = [0 2.1213 4 0]'

y = 4×1

         0
    2.1213
    4.0000
         0

z = [7 8 9 10]'

z = 4×1

     7
     8
     9
    10

[theta,rho,z] = cart2pol(x,y,z)

theta = 4×1

         0
    0.7854
    1.5708
    3.1416

rho = 4×1

    1.0000
    3.0000
    4.0000
    5.0000

z = 4×1

     7
     8
     9
    10

Input Arguments

x, y, z — Cartesian coordinates

scalars | vectors | matrices | multidimensional arrays

Cartesian coordinates, specified as scalars, vectors, matrices, or multidimensional arrays. x, y, and z must be the same size, or have sizes that are compatible (for example, x is an M-by-N matrix, y is a scalar, and z is a scalar or 1-by-N row vector). For more information, see Compatible Array Sizes for Basic Operations.

Data Types: single | double

Output Arguments

theta — Angular coordinate

array

Angular coordinate, returned as an array. theta is the counterclockwise angle in the x-y plane measured in radians from the positive x-axis. The value of the angle is in the range [-pi pi].

rho — Radial coordinate

array

Radial coordinate, returned as an array. rho is the distance from the origin to a point in the x-y plane.

z — Elevation coordinate

array

Elevation coordinate, returned as an array. z is the height above the x-y plane.

Algorithms

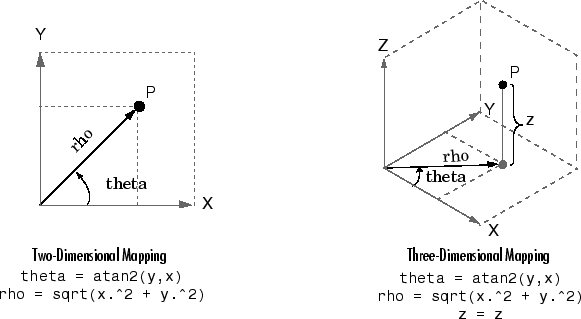
The mapping from two-dimensional Cartesian coordinates to polar coordinates, and from three-dimensional Cartesian coordinates to cylindrical coordinates is

Extended Capabilities

Tall Arrays

Calculate with arrays that have more rows than fit in memory.

The cart2pol function fully supports tall arrays. For more information, see Tall Arrays.

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

• If you use cart2pol with single type and double type operands, the generated code might not produce the same result as MATLAB^®. See Binary Element-Wise Operations with Single and Double Operands (MATLAB Coder).

GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Thread-Based Environment

Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

The cart2pol function fully supports GPU arrays. To run the function on a GPU, specify the input data as a gpuArray (Parallel Computing Toolbox). For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Distributed Arrays

Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

This function fully supports distributed arrays. For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).

Version History

Introduced before R2006a