matlab.tall.transform

Transform array by applying function handle to blocks of data

Syntax

tA = matlab.tall.transform(fcn,tX)

tA = matlab.tall.transform(fcn,tX,tY,...)

[tA,tB,...] = matlab.tall.transform(fcn,tX,tY,...)

[tA,tB,...] = matlab.tall.transform(___,'OutputsLike',{PA,PB,...})

Description

tA = matlab.tall.transform(fcn,tX) applies the function handle fcn to each block of array tX and returns a transformed array, tA.

tA = matlab.tall.transform(fcn,tX,tY,...) specifies several arrays tX,tY,... that are inputs to fcn. The same rows of each array are operated on by fcn; for example, fcn(tX(n:m,:),tY(n:m,:)). Inputs with a height of one are passed to every call of fcn.

[tA,tB,...] = matlab.tall.transform(fcn,tX,tY,...) , where fcn is a function that returns multiple outputs, returns arrays tA,tB,..., each corresponding to one of the output arguments of fcn. All outputs of fcn must have the same height, and the number of outputs must be the same as the number that are requested from matlab.tall.transform.

[tA,tB,...] = matlab.tall.transform(___,'OutputsLike',{PA,PB,...}) specifies that the outputs tA,tB,... have the same data types as the prototype arrays PA,PB,..., respectively. You can use any of the input argument combinations in previous syntaxes.

Examples

Apply Function to Tall Vector

Use matlab.tall.transform to build a tall array of zeros with attributes similar to another array.

Create a tall table for the airlinesmall.csv data set. The data contains information about arrival and departure times of US flights. Extract the ArrDelay variable, which is a vector of arrival delays.

ds = tabularTextDatastore('airlinesmall.csv','TreatAsMissing','NA');
ds.SelectedVariableNames = {'ArrDelay' 'DepDelay'};
tt = tall(ds);
tX = tt.ArrDelay

tX =

  Mx1 tall double column vector

     8
     8
    21
    13
     4
    59
     3
    11
    :
    :

Write an anonymous function that creates an array of zeros with the same size and data type as the input.

zerosLike = @(in) zeros(size(in),'like',in);

Use matlab.tall.transform to apply the zerosLike function to the vector of arrival delays. The result is a tall vector of the same size, but whose values are all zero.

s = matlab.tall.transform(zerosLike, tX)

s =

  Mx1 tall double column vector

     0
     0
     0
     0
     0
     0
     0
     0
     :
     :

Transform Two Vectors

Calculate the mean total flight delay from vectors of arrival and departure delays.

Create a tall table for the airlinesmall.csv data set. The data contains information about arrival and departure times of US flights. Extract the ArrDelay and DepDelay variables, which are vectors of arrival and departure delays.

ds = tabularTextDatastore('airlinesmall.csv','TreatAsMissing','NA');
ds.SelectedVariableNames = {'ArrDelay' 'DepDelay'};
tt = tall(ds);
tX = tt.ArrDelay;
tY = tt.DepDelay;

The meanDelay function concatenates the input vectors into a matrix, sums the values in each row (ignoring NaNs), and then it calculates the mean. Display the contents of that function file.

type meanDelay

function D = meanDelay(a,b)
X = [a b];
Y = sum(X,2,'omitnan');
D = mean(Y);
end

Use matlab.tall.transform to apply the meanDelay function to each block of data in tX and tY. The result is the mean total delay in each block of data.

d = matlab.tall.transform(@meanDelay, tX, tY)

d =

  7x1 tall double column vector

   14.0621
   11.1639
   17.2311
   15.1852
   12.5860
   19.8596
   14.4036

This operation assumes that the result of reducing each block of data to a scalar value can fit in memory. For extremely large data sets and data sets that use a small block size, that assumption might not be true.

Apply Function with Multiple Outputs

Find the maximum value and the index of that value in each row of data.

Create a tall table for the airlinesmall.csv data set. The data contains information about arrival and departure times of US flights. Extract the ArrDelay and DepDelay variables, which are vectors of arrival and departure delays.

ds = tabularTextDatastore('airlinesmall.csv','TreatAsMissing','NA');
ds.SelectedVariableNames = {'ArrDelay' 'DepDelay'};
tt = tall(ds);
tX = tt.ArrDelay;
tY = tt.DepDelay;

The maxDelay function concatenates the input vectors, and then it finds the maximum arrival or departure delay duration and its column index. Display the contents of that file.

type maxDelay

function [M,I] = maxDelay(A,B)
X = [A B];
[M,I] = max(X,[],2);
end

Use matlab.tall.transform to apply the maxDelay function to each block of data in tX and tY. The result is the maximum arrival or departure delay for each row of data, as well as an index vector indicating which column the maximum value came from. An index of 1 indicates that the arrival delay in that row is larger, and an index of 2 indicates that the departure delay is larger.

[M, idx] = matlab.tall.transform(@maxDelay, tX, tY)

M =

  Mx1 tall double column vector

    12
     8
    21
    13
     4
    63
     3
    11
    :
    :


idx =

  Mx1 tall double column vector

     2
     1
     1
     1
     1
     2
     1
     1
     :
     :

Output Table with Different Variables

Use the 'OutputsLike' option to return a table from matlab.tall.transform that has different variables from the input table.

Create a tall table with two variables of random values.

T = tall(table(rand(1e6,1),rand(1e6,1)))

T =

  1,000,000x2 tall table

     Var1       Var2  
    _______    _______

    0.81472    0.90399
    0.90579    0.94095
    0.12699    0.80252
    0.91338    0.24205
    0.63236    0.97566
    0.09754    0.31723
     0.2785    0.81279
    0.54688    0.69743
       :          :
       :          :

The function tableDiff calculates the difference between two input table variables and adds the result as a new variable in the table. Display the contents of the file.

type tableDiff

function Tout = tableDiff(Tin)
d = Tin.Var2 - Tin.Var1;
Tin.Var3 = abs(d);
Tout = Tin;
end

Use matlab.tall.transform to apply the tableDiff function to each block of data in T. Since the output table has different variables from the input table, use the 'OutputsLike' name-value pair to supply a prototype table with similar variables as the output (three variables with the default names Var1, Var2, and Var3).

Z = matlab.tall.transform(@tableDiff, T, 'OutputsLike', {table(1,1,1)})

Z =

  Mx3 tall table

     Var1       Var2        Var3  
    _______    _______    ________

    0.81472    0.90399    0.089267
    0.90579    0.94095    0.035156
    0.12699    0.80252     0.67553
    0.91338    0.24205     0.67133
    0.63236    0.97566      0.3433
    0.09754    0.31723     0.21969
     0.2785    0.81279     0.53429
    0.54688    0.69743     0.15054
       :          :          :
       :          :          :

Input Arguments

fcn — Transform function to apply

function handle | anonymous function

Transform function to apply, specified as a function handle or anonymous function. Each output of fcn must be the same type as the first input tX. You can use the 'OutputsLike' option to return outputs of different data types. If fcn returns more than one output, then the outputs must all have the same height.

The general functional signature of fcn is

[a, b, c, ...] = fcn(x, y, z, ...)

fcn must satisfy these requirements:

1. Input Arguments — The inputs [x, y, z, ...] are blocks of data that fit in memory. The blocks are produced by extracting data from the respective tall array inputs [tX, tY, tZ, ...]. The inputs [x, y, z, ...] satisfy these properties:

   • All of [x, y, z, ...] have the same size in the first dimension after any allowed expansion.

   • The blocks of data in [x, y, z, ...] come from the same index in the tall dimension, assuming the tall array is nonsingleton in the tall dimension. For example, if tX and tY are nonsingleton in the tall dimension, then the first set of blocks might be x = tX(1:20000,:) and y = tY(1:20000,:).

   • If the first dimension of any of [tX, tY, tZ, ...] has a size of 1, then the corresponding block [x, y, z, ...] consists of all the data in that tall array.

2. Output Arguments — The outputs [a, b, c, ...] are blocks that fit in memory, to be sent to the respective outputs [tA, tB, tC, ...]. The outputs [a, b, c, ...] satisfy these properties:

   • All of [a, b, c, ...] must have the same size in the first dimension.

   • All of [a, b, c, ...] are vertically concatenated with the respective results of previous calls to fcn.

   • All of [a, b, c, ...] are sent to the same index in the first dimension in their respective destination output arrays.

3. Functional Rules — fcn must satisfy the functional rule:

   • F([inputs1; inputs2]) == [F(inputs1); F(inputs2)]: Applying the function to the concatenation of the inputs should be the same as applying the function to the inputs separately and then concatenating the results.

4. Empty Inputs — Ensure that fcn can handle an input that has a height of 0. Empty inputs can occur when a file is empty or if you have done a lot of filtering on the data.

For example, this function accepts two input arrays, squares them, and returns two output arrays:

function [xx,yy] = sqInputs(x,y)
xx = x.^2;
yy = y.^2;
end 

After you save this function to an accessible folder, you can invoke the function to square tX and tY with this command:

[tA,tB] = matlab.tall.transform(@sqInputs,tX,tY)

Example: tA = matlab.tall.transform(@(x) x .* 2, tX) specifies an anonymous function to multiply the values in tX by 2.

Example: tC = matlab.tall.transform(@plus,tX,tY) specifies a function handle @plus to add two arrays together.

Data Types: function_handle

tX, tY — Input arrays

scalars | vectors | matrices | multidimensional arrays

Input arrays, specified as scalars, vectors, matrices, or multidimensional arrays. The input arrays are used as inputs to the specified function fcn. Each input array tX,tY,... must have compatible heights. Two inputs have compatible height when they have the same height, or when one input is of height one.

PA, PB — Prototype of output arrays

arrays

Prototype of output arrays, specified as arrays. When you specify 'OutputsLike', the output arrays tA,tB,... returned by matlab.tall.transform have the same data types as the specified arrays {PA,PB,...}.

Example: tA = matlab.tall.transform(fcn,tX,'OutputsLike',{int8(1)});, where tX is a double-precision array, returns A as int8 instead of double.

Output Arguments

tA, tB — Output arrays

scalars | vectors | matrices | multidimensional arrays

Output arrays, returned as scalars, vectors, matrices, or multidimensional arrays. If any input to matlab.tall.transform is tall, then all output arguments are also tall. Otherwise, all output arguments are in-memory arrays.

The size and data type of the output arrays depend on the specified function fcn. In general, the outputs tA,tB,... must all have the same data type as the first input X. However, you can specify 'OutputsLike' to return different data types. The output arrays tA,tB,... all have the same height.

More About

Tall Array Blocks

When you create a tall array from a datastore, the underlying datastore facilitates the movement of data during a calculation. The data moves in discrete pieces called blocks or chunks, where each block is a set of consecutive rows that can fit in memory. For example, one block of a 2-D array (such as a table) is X(n:m,:), for some subscripts n and m. The size of each block is based on the value of the ReadSize property of the datastore, but the block might not be exactly that size. For the purposes of matlab.tall.transform, a tall array is considered to be the vertical concatenation of many such blocks:

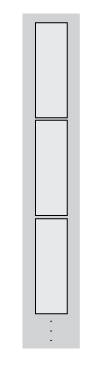
For example, if you use the sum function as the transform function, the result is the sum per block. Therefore, instead of returning a single scalar value for the sum of the elements, the result is a vector with length equal to the number of blocks.

ds = tabularTextDatastore('airlinesmall.csv','TreatAsMissing','NA');
ds.SelectedVariableNames = {'ArrDelay' 'DepDelay'};
tt = tall(ds);
tX = tt.ArrDelay;

f = @(x) sum(x,'omitnan');
s = matlab.tall.transform(f, tX);
s = gather(s)

s =

      140467
      101065
      164355
      135920
      111182
      186274
       21321

Version History

Introduced in R2018b