`fmincon` Interior-Point Algorithm with Analytic Hessian

Open Live Script

This example shows how to use derivative information to make the solution process faster and more robust. The fmincon interior-point algorithm can accept a Hessian function as an input. When you supply a Hessian, you can obtain a faster, more accurate solution to a constrained minimization problem.

The helper function bigtoleft is an objective function that grows rapidly negative as the x(1) coordinate becomes negative. Its gradient is a three-element vector. The code for the bigtoleft helper function appears at the end of this example.

The constraint set for this example is the intersection of the interiors of two cones—one pointing up, and one pointing down. The constraint function is a two-component vector containing one component for each cone. Because this example is three-dimensional, the gradient of the constraint is a 3-by-2 matrix. The code for the twocone helper function appears at the end of this example.

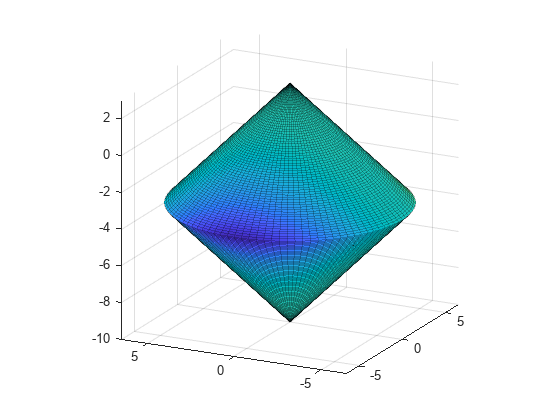
Create a figure of the constraints, colored using the objective function.

% Create figure
figure1 = figure;

% Create axes
axes1 = axes('Parent',figure1);
view([-63.5 18]);
grid('on');
hold('on');

% Set up polar coordinates and two cones
r=0:.1:6.5;
th=2*pi*(0:.01:1);
x=r'*cos(th);
y=r'*sin(th);
z=-10+sqrt(x.^2+y.^2);
zz=3-sqrt(x.^2+y.^2);

% Evaluate objective function on cone surfaces
newxf=reshape(bigtoleft([x(:),y(:),z(:)]),66,101)/3000;
newxg=reshape(bigtoleft([x(:),y(:),z(:)]),66,101)/3000;

% Create lower surf with color set by objective
surf(x,y,z,newxf,'Parent',axes1,'EdgeAlpha',0.25);

% Create upper surf with color set by objective
surf(x,y,zz,newxg,'Parent',axes1,'EdgeAlpha',0.25);
axis equal

Figure contains an axes object. The axes object contains 2 objects of type surface.

Create Hessian Function

To use second-order derivative information in the fmincon solver, you must create a Hessian that is the Hessian of the Lagrangian. The Hessian of the Lagrangian is given by the equation

$\nabla_{x x}^{2} L (x, λ) = \nabla^{2} f (x) + \sum λ_{i} \nabla^{2} c_{i} (x) + \sum λ_{i} \nabla^{2} c e q_{i} (x) .$

Here, $f (x)$ is the bigtoleft function, and the $c_{i} (x)$ are the two cone constraint functions. The hessinterior helper function at the end of this example computes the Hessian of the Lagrangian at a point x with the Lagrange multiplier structure lambda. The function first computes $\nabla^{2} f (x)$ . It then computes the two constraint Hessians $\nabla^{2} c_{1} (x)$ and $\nabla^{2} c_{2} (x)$ , multiplies them by their corresponding Lagrange multipliers lambda.ineqnonlin(1) and lambda.ineqnonlin(2), and adds them. You can see from the definition of the twocone constraint function that $\nabla^{2} c_{1} (x) = \nabla^{2} c_{2} (x)$ , which simplifies the calculation.

Create Options to Use Derivatives

To enable fmincon to use the objective gradient, constraint gradients, and Hessian, you must set appropriate options. The HessianFcn option using the Hessian of the Lagrangian is available only for the interior-point algorithm.

options = optimoptions('fmincon','Algorithm','interior-point',...
    "SpecifyConstraintGradient",true,"SpecifyObjectiveGradient",true,...
    'HessianFcn',@hessinterior);

Minimize Using All Derivative Information

Set the initial point x0 = [-1,-1,-1].

x0 = [-1,-1,-1];

The problem has no linear constraints or bounds. Set those arguments to [].

A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];

Solve the problem.

[x,fval,eflag,output] = fmincon(@bigtoleft,x0,...
           A,b,Aeq,beq,lb,ub,@twocone,options);

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

Examine Solution and Solution Process

Examine the solution, objective function value, exit flag, and number of function evaluations and iterations.

disp(x)

   -6.5000   -0.0000   -3.5000

disp(fval)

  -2.8941e+03

disp(eflag)

disp([output.funcCount,output.iterations])

     7     6

If you do not use a Hessian function, fmincon takes more iterations to converge and requires more function evaluations.

options.HessianFcn = [];
[x2,fval2,eflag2,output2] = fmincon(@bigtoleft,x0,...
           A,b,Aeq,beq,lb,ub,@twocone,options);

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

disp([output2.funcCount,output2.iterations])

    13     9

If you also do not include the gradient information, fmincon takes the same number of iterations, but requires many more function evaluations.

options.SpecifyConstraintGradient = false;
options.SpecifyObjectiveGradient = false;
[x3,fval3,eflag3,output3] = fmincon(@bigtoleft,x0,...
           A,b,Aeq,beq,lb,ub,@twocone,options);

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

disp([output3.funcCount,output3.iterations])

    43     9

Helper Functions

This code creates the bigtoleft helper function.

function [f gradf] = bigtoleft(x)
% This is a simple function that grows rapidly negative
% as x(1) becomes negative
%
f = 10*x(:,1).^3+x(:,1).*x(:,2).^2+x(:,3).*(x(:,1).^2+x(:,2).^2);

if nargout > 1

   gradf=[30*x(1)^2+x(2)^2+2*x(3)*x(1);
       2*x(1)*x(2)+2*x(3)*x(2);
       (x(1)^2+x(2)^2)];

end
end

This code creates the twocone helper function.

function [c ceq gradc gradceq] = twocone(x)
% This constraint is two cones, z > -10 + r
% and z < 3 - r

ceq = [];
r = sqrt(x(1)^2 + x(2)^2);
c = [-10+r-x(3);
    x(3)-3+r];

if nargout > 2

    gradceq = [];
    gradc = [x(1)/r,x(1)/r;
       x(2)/r,x(2)/r;
       -1,1];

end
end

This code creates the hessinterior helper function.

function h = hessinterior(x,lambda)

h = [60*x(1)+2*x(3),2*x(2),2*x(1);
    2*x(2),2*(x(1)+x(3)),2*x(2);
    2*x(1),2*x(2),0];% Hessian of f
r = sqrt(x(1)^2+x(2)^2);% radius
rinv3 = 1/r^3;
hessc = [(x(2))^2*rinv3,-x(1)*x(2)*rinv3,0;
    -x(1)*x(2)*rinv3,x(1)^2*rinv3,0;
    0,0,0];% Hessian of both c(1) and c(2)
h = h + lambda.ineqnonlin(1)*hessc + lambda.ineqnonlin(2)*hessc;
end