OptimizationValues
Description
Creation
The solve function returns a vector of
OptimizationValues objects as the solution to a multiobjective
problem.
Create an OptimizationValues object for a start point
x0 by using the optimvalues
function.
Properties
Object Functions
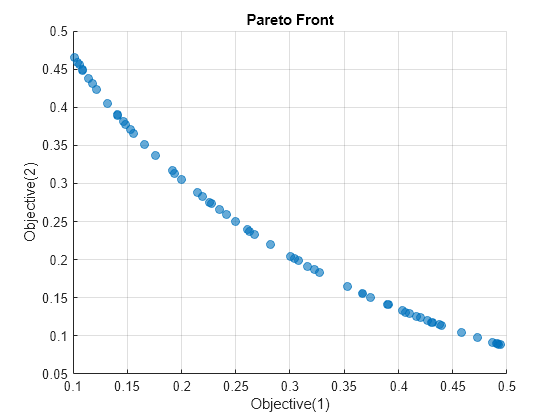
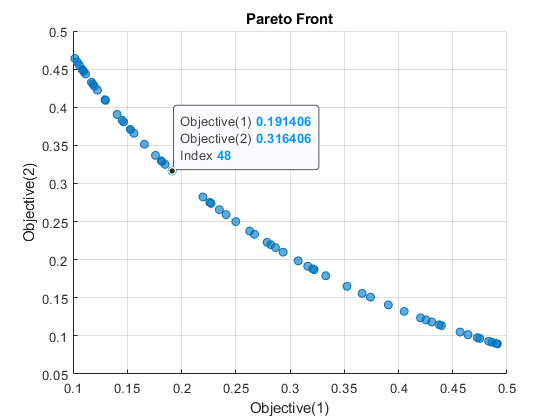
paretoplot | Pareto plot of multiobjective values |
Examples
Limitations
OptimizationValuesobjects support horizontal concatenation only. In other words, you can have only row vectors ofOptimizationValuesobjects.
Version History
Introduced in R2022a
See Also
Topics
- Specify Start Points for MultiStart, Problem-Based (Global Optimization Toolbox)
- Pareto Front for Multiobjective Optimization, Problem-Based (Global Optimization Toolbox)