polellip
Parameters of ellipse traced out by tip of a polarized field vector
Syntax
Description
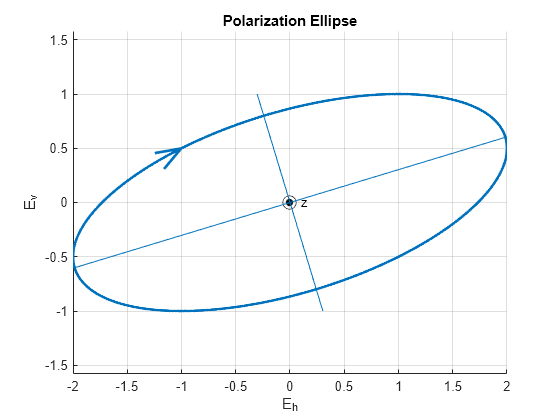
tau = polellip(fv)fv. fv contains
the linear polarization components of a field in either one of two
forms: (1) each column represents a field in the form of [Eh;Ev],
where Eh and Ev are the field’s
horizontal and vertical linear polarization components or (2) each
column contains the polarization ratio, Ev/Eh.
The expression of a field in terms of a two-row vector of linear polarization
components is called the Jones vector formalism.
[ returns, in addition,
a row vector, tau,epsilon]
= polellip(fv)epsilon, containing the ellipticity
angle (in degrees) of the polarization ellipses. The ellipticity
angle is the angle determined by the ratio of the length of the semi-minor
axis to semi-major axis and lies in the range [-45°,45°].
This syntax can use any of the input arguments in the previous syntax.
[ returns, in addition,
a row vector, tau,epsilon,ar]
= polellip(fv)ar, containing the axial ratios
of the polarization ellipses. The axial ratio is defined as the ratio
of the lengths of the semi-major axis of the ellipse to the semi-minor
axis. This syntax can use any of the input arguments in the previous
syntaxes.
[ returns, in addition,
a cell array of character vectors, tau,epsilon,ar,rs]
= polellip(fv)rs, containing
the rotation senses of the polarization ellipses. Each entry in the
array is one of 'Linear', 'Left Circular', 'Right
Circular', 'Left Elliptical' or 'Right
Elliptical'. This syntax can use any of the input arguments
in the previous syntaxes.
Examples
Input Arguments
Output Arguments
References
[1] Mott, H., Antennas for Radar and Communications, John Wiley & Sons, 1992.
[2] Jackson, J.D. , Classical Electrodynamics, 3rd Edition, John Wiley & Sons, 1998, pp. 299–302
[3] Born, M. and E. Wolf, Principles of Optics, 7th Edition, Cambridge: Cambridge University Press, 1999, pp 25–32.
Extended Capabilities
Version History
Introduced in R2013a
See Also
circpol2pol | pol2circpol | polratio | stokes