tsaresidual
Residual signal of a time-synchronous averaged signal
Syntax
Description
Y = tsaresidual(X,fs,rpm,orderList)Y of the time-synchronous averaged (TSA)
signal vector X using sampling rate fs, the
rotational speed rpm, and the orders to be filtered
orderList. The residual signal is computed by removing the
components in orderList and their harmonics from
X. You can use Y to further extract condition
indicators of rotating machinery for predictive maintenance. For example, extracting the
root-mean-squared value of the residual signal is useful in identifying changes over time
which indicate potential machine faults.
___ = tsaresidual(___,
allows you to specify additional parameters using one or more name-value pair arguments.
You can use this syntax with any of the previous input and output arguments.Name,Value)
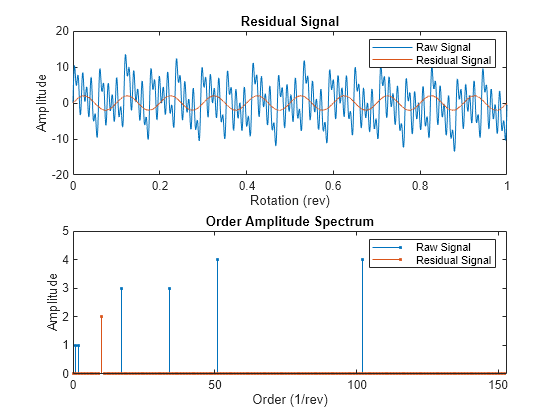
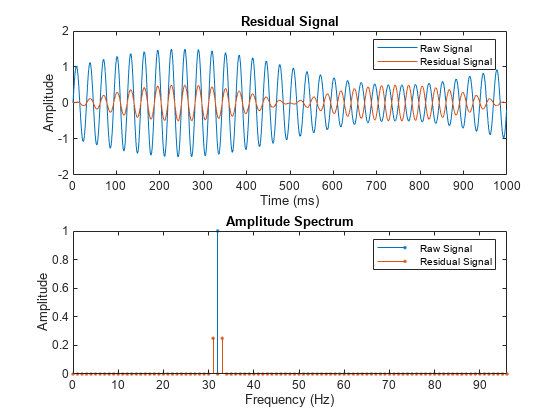
tsaresidual(___) with no output arguments plots the
time-domain and frequency-domain plots of the raw and residual TSA signals.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
Residual Signal
The residual signal is computed from the TSA signal by removing the following from the signal spectrum:
Shaft frequency and its harmonics
Gear meshing frequencies and their harmonics
The frequencies are removed by computing the discrete Fourier transform (DFT)
and setting the spectrum values to zero at the specified frequencies.
tsaresidual uses a bandwidth equal to the shaft speed around the
frequencies of interest to filter out the undesired frequency components, as mentioned in
[4].
Amplitude Spectrum
The amplitude spectrum of the residual signal is computed as follows,
Here, Y is the residual signal.
References
[1] McFadden, P.D. "Examination of a Technique for the Early Detection of Failure in Gears by Signal Processing of the Time Domain Average of the Meshing Vibration." Aero Propulsion Technical Memorandum 434. Melbourne, Australia: Aeronautical Research Laboratories, Apr. 1986.
[2] Večeř, P., Marcel Kreidl, and R. Šmíd. "Condition Indicators for Gearbox Monitoring Systems." Acta Polytechnica 45.6 (2005), pages 35-43.
[3] Zakrajsek, J. J., Townsend, D. P., and Decker, H. J. "An Analysis of Gear Fault Detection Methods as Applied to Pitting Fatigue Failure Data." Technical Memorandum 105950. NASA, Apr. 1993.
[4] Zakrajsek, James J. "An investigation of gear mesh failure prediction techniques." National Aeronautics and Space Administration Cleveland OH Lewis Research Center, 1989. No. NASA-E-5049.
Extended Capabilities
Version History
Introduced in R2018b