validatemodel
Validate quality of compact credit scorecard model
Syntax
Description
Stats = validatemodel(csc,data)compactCreditScorecard model for the data set specified using
the argument data.
[
specifies options using one or more name-value pair arguments in addition to
the input arguments in the previous syntax and returns the outputs
Stats,T]
= validatemodel(___,Name,Value)Stats and T.
[
specifies options using one or more name-value pair arguments in addition to
the input arguments in the previous syntax and returns the outputs
Stats,T,hf]
= validatemodel(___,Name,Value)Stats and T and the figure
handle hf to the CAP, ROC, and KS plots.
Examples
Compute model validation statistics for a compact credit scorecard model.
To create a compactCreditScorecard object, you must first develop a credit scorecard model using a creditscorecard object.
Create a creditscorecard object using the CreditCardData.mat file to load the data (using a dataset from Refaat 2011).
load CreditCardData.mat sc = creditscorecard(data, 'IDVar','CustID')
sc =
creditscorecard with properties:
GoodLabel: 0
ResponseVar: 'status'
WeightsVar: ''
VarNames: {'CustID' 'CustAge' 'TmAtAddress' 'ResStatus' 'EmpStatus' 'CustIncome' 'TmWBank' 'OtherCC' 'AMBalance' 'UtilRate' 'status'}
NumericPredictors: {'CustAge' 'TmAtAddress' 'CustIncome' 'TmWBank' 'AMBalance' 'UtilRate'}
CategoricalPredictors: {'ResStatus' 'EmpStatus' 'OtherCC'}
BinMissingData: 0
IDVar: 'CustID'
PredictorVars: {'CustAge' 'TmAtAddress' 'ResStatus' 'EmpStatus' 'CustIncome' 'TmWBank' 'OtherCC' 'AMBalance' 'UtilRate'}
Data: [1200×11 table]
Perform automatic binning using the default options. By default, autobinning uses the Monotone algorithm.
sc = autobinning(sc);
Fit the model.
sc = fitmodel(sc);
1. Adding CustIncome, Deviance = 1490.8527, Chi2Stat = 32.588614, PValue = 1.1387992e-08
2. Adding TmWBank, Deviance = 1467.1415, Chi2Stat = 23.711203, PValue = 1.1192909e-06
3. Adding AMBalance, Deviance = 1455.5715, Chi2Stat = 11.569967, PValue = 0.00067025601
4. Adding EmpStatus, Deviance = 1447.3451, Chi2Stat = 8.2264038, PValue = 0.0041285257
5. Adding CustAge, Deviance = 1441.994, Chi2Stat = 5.3511754, PValue = 0.020708306
6. Adding ResStatus, Deviance = 1437.8756, Chi2Stat = 4.118404, PValue = 0.042419078
7. Adding OtherCC, Deviance = 1433.707, Chi2Stat = 4.1686018, PValue = 0.041179769
Generalized linear regression model:
logit(status) ~ 1 + CustAge + ResStatus + EmpStatus + CustIncome + TmWBank + OtherCC + AMBalance
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
________ ________ ______ __________
(Intercept) 0.70239 0.064001 10.975 5.0538e-28
CustAge 0.60833 0.24932 2.44 0.014687
ResStatus 1.377 0.65272 2.1097 0.034888
EmpStatus 0.88565 0.293 3.0227 0.0025055
CustIncome 0.70164 0.21844 3.2121 0.0013179
TmWBank 1.1074 0.23271 4.7589 1.9464e-06
OtherCC 1.0883 0.52912 2.0569 0.039696
AMBalance 1.045 0.32214 3.2439 0.0011792
1200 observations, 1192 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 89.7, p-value = 1.4e-16
Format the unscaled points.
sc = formatpoints(sc, 'PointsOddsAndPDO',[500,2,50]);Convert the creditscorecard object into a compactCreditScorecard object. A compactCreditScorecard object is a lightweight version of a creditscorecard object that is used for deployment purposes.
csc = compactCreditScorecard(sc);
Validate the compact credit scorecard model by generating the CAP, ROC, and KS plots. This example uses the training data. However, you can use any validation data, as long as:
The data has the same predictor names and predictor types as the data used to create the initial
creditscorecardobject.The data has a response column with the same name as the
'ResponseVar'property in the initialcreditscorecardobject.The data has a weights column (if weights were used to train the model) with the same name as
'WeightsVar'property in the initialcreditscorecardobject.
[Stats,T] = validatemodel(csc,data,'Plot',{'CAP','ROC','KS'});



disp(Stats)
Measure Value
________________________ _______
{'Accuracy Ratio' } 0.32258
{'Area under ROC curve'} 0.66129
{'KS statistic' } 0.2246
{'KS score' } 499.62
disp(T(1:15,:))
Scores ProbDefault TrueBads FalseBads TrueGoods FalseGoods Sensitivity FalseAlarm PctObs
______ ___________ ________ _________ _________ __________ ___________ __________ __________
369.54 0.75313 0 1 802 397 0 0.0012453 0.00083333
378.19 0.73016 1 1 802 396 0.0025189 0.0012453 0.0016667
380.28 0.72444 2 1 802 395 0.0050378 0.0012453 0.0025
391.49 0.69234 3 1 802 394 0.0075567 0.0012453 0.0033333
395.57 0.68017 4 1 802 393 0.010076 0.0012453 0.0041667
396.14 0.67846 4 2 801 393 0.010076 0.0024907 0.005
396.45 0.67752 5 2 801 392 0.012594 0.0024907 0.0058333
398.61 0.67094 6 2 801 391 0.015113 0.0024907 0.0066667
398.68 0.67072 7 2 801 390 0.017632 0.0024907 0.0075
401.33 0.66255 8 2 801 389 0.020151 0.0024907 0.0083333
402.66 0.65842 8 3 800 389 0.020151 0.003736 0.0091667
404.25 0.65346 9 3 800 388 0.02267 0.003736 0.01
404.73 0.65193 9 4 799 388 0.02267 0.0049813 0.010833
405.53 0.64941 11 4 799 386 0.027708 0.0049813 0.0125
405.7 0.64887 11 5 798 386 0.027708 0.0062267 0.013333
Compute model validation statistics for a compact credit scorecard model with weights.
To create a compactCreditScorecard object, you must first develop a credit scorecard model using a creditscorecard object.
Use the CreditCardData.mat file to load the data (dataWeights) that contains a column (RowWeights) for the weights (using a dataset from Refaat 2011).
load CreditCardData.matCreate a creditscorecard object using the optional name-value pair argument 'WeightsVar'.
sc = creditscorecard(dataWeights,'IDVar','CustID','WeightsVar','RowWeights')
sc =
creditscorecard with properties:
GoodLabel: 0
ResponseVar: 'status'
WeightsVar: 'RowWeights'
VarNames: {'CustID' 'CustAge' 'TmAtAddress' 'ResStatus' 'EmpStatus' 'CustIncome' 'TmWBank' 'OtherCC' 'AMBalance' 'UtilRate' 'RowWeights' 'status'}
NumericPredictors: {'CustAge' 'TmAtAddress' 'CustIncome' 'TmWBank' 'AMBalance' 'UtilRate'}
CategoricalPredictors: {'ResStatus' 'EmpStatus' 'OtherCC'}
BinMissingData: 0
IDVar: 'CustID'
PredictorVars: {'CustAge' 'TmAtAddress' 'ResStatus' 'EmpStatus' 'CustIncome' 'TmWBank' 'OtherCC' 'AMBalance' 'UtilRate'}
Data: [1200×12 table]
Perform automatic binning. By default, autobinning uses the Monotone algorithm.
sc = autobinning(sc)
sc =
creditscorecard with properties:
GoodLabel: 0
ResponseVar: 'status'
WeightsVar: 'RowWeights'
VarNames: {'CustID' 'CustAge' 'TmAtAddress' 'ResStatus' 'EmpStatus' 'CustIncome' 'TmWBank' 'OtherCC' 'AMBalance' 'UtilRate' 'RowWeights' 'status'}
NumericPredictors: {'CustAge' 'TmAtAddress' 'CustIncome' 'TmWBank' 'AMBalance' 'UtilRate'}
CategoricalPredictors: {'ResStatus' 'EmpStatus' 'OtherCC'}
BinMissingData: 0
IDVar: 'CustID'
PredictorVars: {'CustAge' 'TmAtAddress' 'ResStatus' 'EmpStatus' 'CustIncome' 'TmWBank' 'OtherCC' 'AMBalance' 'UtilRate'}
Data: [1200×12 table]
Fit the model.
sc = fitmodel(sc);
1. Adding CustIncome, Deviance = 764.3187, Chi2Stat = 15.81927, PValue = 6.968927e-05
2. Adding TmWBank, Deviance = 751.0215, Chi2Stat = 13.29726, PValue = 0.0002657942
3. Adding AMBalance, Deviance = 743.7581, Chi2Stat = 7.263384, PValue = 0.007037455
Generalized linear regression model:
logit(status) ~ 1 + CustIncome + TmWBank + AMBalance
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
________ ________ ______ __________
(Intercept) 0.70642 0.088702 7.964 1.6653e-15
CustIncome 1.0268 0.25758 3.9862 6.7132e-05
TmWBank 1.0973 0.31294 3.5063 0.0004543
AMBalance 1.0039 0.37576 2.6717 0.0075464
1200 observations, 1196 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 36.4, p-value = 6.22e-08
Format the unscaled points.
sc = formatpoints(sc,'PointsOddsAndPDO',[500,2,50]);Convert the creditscorecard object into a compactCreditScorecard object. A compactCreditScorecard object is a lightweight version of a creditscorecard object that is used for deployment purposes.
csc = compactCreditScorecard(sc);
Validate the compact credit scorecard model by generating the CAP, ROC, and KS plots. When you use the optional name-value pair argument 'WeightsVar' to specify observation (sample) weights in the original creditscorecard object, the T table for validatemodel uses statistics, sums, and cumulative sums that are weighted counts.
This example uses the training data (dataWeights). However, you can use any validation data, as long as:
The data has the same predictor names and predictor types as the data used to create the initial
creditscorecardobject.The data has a response column with the same name as the
'ResponseVar'property in the initialcreditscorecardobject.The data has a weights column (if weights were used to train the model) with the same name as the
'WeightsVar'property in the initialcreditscorecardobject.
[Stats,T] = validatemodel(csc,dataWeights,'Plot',{'CAP','ROC','KS'});
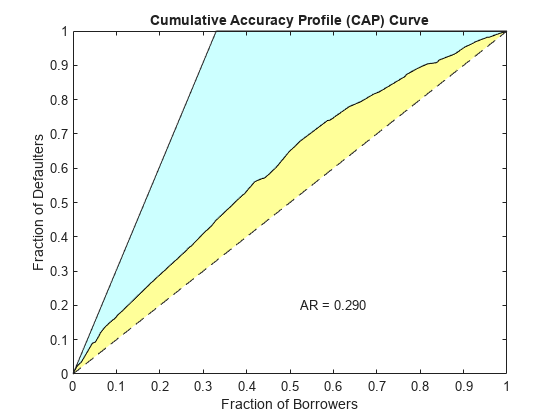
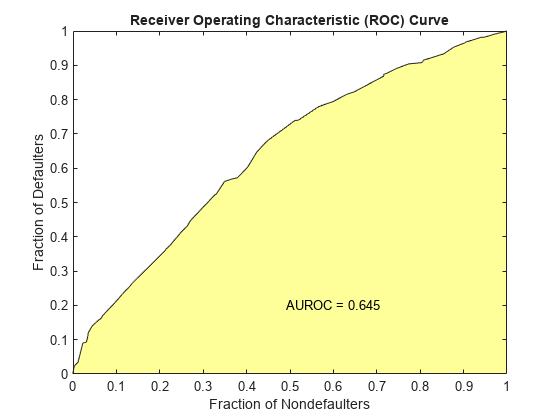

Stats
Stats=4×2 table
Measure Value
________________________ _______
{'Accuracy Ratio' } 0.28972
{'Area under ROC curve'} 0.64486
{'KS statistic' } 0.23215
{'KS score' } 505.41
T(1:10,:)
ans=10×9 table
Scores ProbDefault TrueBads FalseBads TrueGoods FalseGoods Sensitivity FalseAlarm PctObs
______ ___________ ________ _________ _________ __________ ___________ __________ _________
401.34 0.66253 1.0788 0 411.95 201.95 0.0053135 0 0.0017542
407.59 0.64289 4.8363 1.2768 410.67 198.19 0.023821 0.0030995 0.0099405
413.79 0.62292 6.9469 4.6942 407.25 196.08 0.034216 0.011395 0.018929
420.04 0.60236 18.459 9.3899 402.56 184.57 0.090918 0.022794 0.045285
437.27 0.544 18.459 10.514 401.43 184.57 0.090918 0.025523 0.047113
442.83 0.52481 18.973 12.794 399.15 184.06 0.093448 0.031057 0.051655
446.19 0.51319 22.396 14.15 397.8 180.64 0.11031 0.034349 0.059426
449.08 0.50317 24.325 14.405 397.54 178.71 0.11981 0.034968 0.062978
449.73 0.50095 28.246 18.049 393.9 174.78 0.13912 0.043813 0.075279
452.44 0.49153 31.511 23.565 388.38 171.52 0.1552 0.057204 0.089557
Compute model validation statistics and assign points for missing data when using the 'BinMissingData' option.
Predictors in a
creditscorecardobject that have missing data in the training set have an explicit bin for<missing>with corresponding points in the final scorecard. These points are computed from the Weight-of-Evidence (WOE) value for the<missing>bin and the logistic model coefficients. For scoring purposes, these points are assigned to missing values and to out-of-range values, and after you convert thecreditscorecardobject to acompactCreditScorecardobject, you can use the final score to compute model validation statistics withvalidatemodel.Predictors in a
creditscorecardobject with no missing data in the training set have no<missing>bin, so no WOE can be estimated from the training data. By default, the points for missing and out-of-range values are set toNaNresulting in a score ofNaNwhen runningscore. For predictors in acreditscorecardobject that have no explicit<missing>bin, use the name-value argument'Missing'informatpointsto specify how the function treats missing data for scoring purposes. After converting thecreditscorecardobject to acompactCreditScorecardobject, you can use the final score to compute model validation statistics withvalidatemodel.
To create a compactCreditScorecard object, you must first develop a credit scorecard model using a creditscorecard object.
Create a creditscorecard object using the CreditCardData.mat file to load dataMissing, a table that contains missing values.
load CreditCardData.mat
head(dataMissing,5) CustID CustAge TmAtAddress ResStatus EmpStatus CustIncome TmWBank OtherCC AMBalance UtilRate status
______ _______ ___________ ___________ _________ __________ _______ _______ _________ ________ ______
1 53 62 <undefined> Unknown 50000 55 Yes 1055.9 0.22 0
2 61 22 Home Owner Employed 52000 25 Yes 1161.6 0.24 0
3 47 30 Tenant Employed 37000 61 No 877.23 0.29 0
4 NaN 75 Home Owner Employed 53000 20 Yes 157.37 0.08 0
5 68 56 Home Owner Employed 53000 14 Yes 561.84 0.11 0
Use creditscorecard with the name-value argument 'BinMissingData' set to true to bin the missing numeric or categorical data in a separate bin. Apply automatic binning.
sc = creditscorecard(dataMissing,'IDVar','CustID','BinMissingData',true); sc = autobinning(sc); disp(sc)
creditscorecard with properties:
GoodLabel: 0
ResponseVar: 'status'
WeightsVar: ''
VarNames: {'CustID' 'CustAge' 'TmAtAddress' 'ResStatus' 'EmpStatus' 'CustIncome' 'TmWBank' 'OtherCC' 'AMBalance' 'UtilRate' 'status'}
NumericPredictors: {'CustAge' 'TmAtAddress' 'CustIncome' 'TmWBank' 'AMBalance' 'UtilRate'}
CategoricalPredictors: {'ResStatus' 'EmpStatus' 'OtherCC'}
BinMissingData: 1
IDVar: 'CustID'
PredictorVars: {'CustAge' 'TmAtAddress' 'ResStatus' 'EmpStatus' 'CustIncome' 'TmWBank' 'OtherCC' 'AMBalance' 'UtilRate'}
Data: [1200×11 table]
To make any negative age or income information invalid or "out of range," set a minimum value of zero for 'CustAge' and 'CustIncome'. For scoring and probability-of-default computations, out-of-range values are given the same points as missing values.
sc = modifybins(sc,'CustAge','MinValue',0); sc = modifybins(sc,'CustIncome','MinValue',0);
Display bin information for numeric data for 'CustAge' that includes missing data in a separate bin labelled <missing>.
bi = bininfo(sc,'CustAge');
disp(bi) Bin Good Bad Odds WOE InfoValue
_____________ ____ ___ ______ ________ __________
{'[0,33)' } 69 52 1.3269 -0.42156 0.018993
{'[33,37)' } 63 45 1.4 -0.36795 0.012839
{'[37,40)' } 72 47 1.5319 -0.2779 0.0079824
{'[40,46)' } 172 89 1.9326 -0.04556 0.0004549
{'[46,48)' } 59 25 2.36 0.15424 0.0016199
{'[48,51)' } 99 41 2.4146 0.17713 0.0035449
{'[51,58)' } 157 62 2.5323 0.22469 0.0088407
{'[58,Inf]' } 93 25 3.72 0.60931 0.032198
{'<missing>'} 19 11 1.7273 -0.15787 0.00063885
{'Totals' } 803 397 2.0227 NaN 0.087112
Display bin information for categorical data for 'ResStatus' that includes missing data in a separate bin labelled <missing>.
bi = bininfo(sc,'ResStatus');
disp(bi) Bin Good Bad Odds WOE InfoValue
______________ ____ ___ ______ _________ __________
{'Tenant' } 296 161 1.8385 -0.095463 0.0035249
{'Home Owner'} 352 171 2.0585 0.017549 0.00013382
{'Other' } 128 52 2.4615 0.19637 0.0055808
{'<missing>' } 27 13 2.0769 0.026469 2.3248e-05
{'Totals' } 803 397 2.0227 NaN 0.0092627
For the 'CustAge' and 'ResStatus' predictors, the training data contains missing data (NaNs and <undefined> values. For missing data in these predictors, the binning process estimates WOE values of -0.15787 and 0.026469, respectively.
Because the training data contains no missing values for the 'EmpStatus' and 'CustIncome' predictors, neither predictor has an explicit bin for missing values.
bi = bininfo(sc,'EmpStatus');
disp(bi) Bin Good Bad Odds WOE InfoValue
____________ ____ ___ ______ ________ _________
{'Unknown' } 396 239 1.6569 -0.19947 0.021715
{'Employed'} 407 158 2.5759 0.2418 0.026323
{'Totals' } 803 397 2.0227 NaN 0.048038
bi = bininfo(sc,'CustIncome');
disp(bi) Bin Good Bad Odds WOE InfoValue
_________________ ____ ___ _______ _________ __________
{'[0,29000)' } 53 58 0.91379 -0.79457 0.06364
{'[29000,33000)'} 74 49 1.5102 -0.29217 0.0091366
{'[33000,35000)'} 68 36 1.8889 -0.06843 0.00041042
{'[35000,40000)'} 193 98 1.9694 -0.026696 0.00017359
{'[40000,42000)'} 68 34 2 -0.011271 1.0819e-05
{'[42000,47000)'} 164 66 2.4848 0.20579 0.0078175
{'[47000,Inf]' } 183 56 3.2679 0.47972 0.041657
{'Totals' } 803 397 2.0227 NaN 0.12285
Use fitmodel to fit a logistic regression model using Weight of Evidence (WOE) data. fitmodel internally transforms all the predictor variables into WOE values by using the bins found in the automatic binning process. fitmodel then fits a logistic regression model using a stepwise method (by default). For predictors that have missing data, there is an explicit <missing> bin, with a corresponding WOE value computed from the data. When you use fitmodel, the function applies the corresponding WOE value for the <missing> bin when performing the WOE transformation.
[sc,mdl] = fitmodel(sc);
1. Adding CustIncome, Deviance = 1490.8527, Chi2Stat = 32.588614, PValue = 1.1387992e-08
2. Adding TmWBank, Deviance = 1467.1415, Chi2Stat = 23.711203, PValue = 1.1192909e-06
3. Adding AMBalance, Deviance = 1455.5715, Chi2Stat = 11.569967, PValue = 0.00067025601
4. Adding EmpStatus, Deviance = 1447.3451, Chi2Stat = 8.2264038, PValue = 0.0041285257
5. Adding CustAge, Deviance = 1442.8477, Chi2Stat = 4.4974731, PValue = 0.033944979
6. Adding ResStatus, Deviance = 1438.9783, Chi2Stat = 3.86941, PValue = 0.049173805
7. Adding OtherCC, Deviance = 1434.9751, Chi2Stat = 4.0031966, PValue = 0.045414057
Generalized linear regression model:
logit(status) ~ 1 + CustAge + ResStatus + EmpStatus + CustIncome + TmWBank + OtherCC + AMBalance
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
________ ________ ______ __________
(Intercept) 0.70229 0.063959 10.98 4.7498e-28
CustAge 0.57421 0.25708 2.2335 0.025513
ResStatus 1.3629 0.66952 2.0356 0.04179
EmpStatus 0.88373 0.2929 3.0172 0.002551
CustIncome 0.73535 0.2159 3.406 0.00065929
TmWBank 1.1065 0.23267 4.7556 1.9783e-06
OtherCC 1.0648 0.52826 2.0156 0.043841
AMBalance 1.0446 0.32197 3.2443 0.0011775
1200 observations, 1192 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 88.5, p-value = 2.55e-16
Scale the scorecard points by the "points, odds, and points to double the odds (PDO)" method using the 'PointsOddsAndPDO' argument of formatpoints. Suppose that you want a score of 500 points to have odds of 2 (twice as likely to be good than to be bad) and that the odds double every 50 points (so that 550 points would have odds of 4).
Display the scorecard showing the scaled points for predictors retained in the fitting model.
sc = formatpoints(sc,'PointsOddsAndPDO',[500 2 50]);
PointsInfo = displaypoints(sc)PointsInfo=38×3 table
Predictors Bin Points
_____________ ______________ ______
{'CustAge' } {'[0,33)' } 54.062
{'CustAge' } {'[33,37)' } 56.282
{'CustAge' } {'[37,40)' } 60.012
{'CustAge' } {'[40,46)' } 69.636
{'CustAge' } {'[46,48)' } 77.912
{'CustAge' } {'[48,51)' } 78.86
{'CustAge' } {'[51,58)' } 80.83
{'CustAge' } {'[58,Inf]' } 96.76
{'CustAge' } {'<missing>' } 64.984
{'ResStatus'} {'Tenant' } 62.138
{'ResStatus'} {'Home Owner'} 73.248
{'ResStatus'} {'Other' } 90.828
{'ResStatus'} {'<missing>' } 74.125
{'EmpStatus'} {'Unknown' } 58.807
{'EmpStatus'} {'Employed' } 86.937
{'EmpStatus'} {'<missing>' } NaN
⋮
Notice that points for the <missing> bin for 'CustAge' and 'ResStatus' are explicitly shown (as 64.9836 and 74.1250, respectively). The function computes these points from the WOE value for the <missing> bin and the logistic model coefficients.
For predictors that have no missing data in the training set, there is no explicit <missing> bin during the training of the model. By default, displaypoints reports the points as NaN for missing data resulting in a score of NaN when you use score. For these predictors, use the name-value pair argument 'Missing' in formatpoints to indicate how missing data should be treated for scoring purposes.
Use compactCreditScorecard to convert the creditscorecard object into a compactCreditScorecard object. A compactCreditScorecard object is a lightweight version of a creditscorecard object that is used for deployment purposes.
csc = compactCreditScorecard(sc);
For the purpose of illustration, take a few rows from the original data as test data and introduce some missing data. Also introduce some invalid, or out-of-range, values. For numeric data, values below the minimum (or above the maximum) are considered invalid, such as a negative value for age (recall that in a previous step, you set 'MinValue' to 0 for 'CustAge' and 'CustIncome'). For categorical data, invalid values are categories not explicitly included in the scorecard, for example, a residential status not previously mapped to scorecard categories, such as "House", or a meaningless string such as "abc123."
This example uses a very small validation data set only to illustrate the scoring of rows with missing and out-of-range values and the relationship between scoring and model validation.
tdata = dataMissing(11:200,mdl.PredictorNames); % Keep only the predictors retained in the model tdata.status = dataMissing.status(11:200); % Copy the response variable value, needed for validation purposes % Set some missing values tdata.CustAge(1) = NaN; tdata.ResStatus(2) = missing; tdata.EmpStatus(3) = missing; tdata.CustIncome(4) = NaN; % Set some invalid values tdata.CustAge(5) = -100; tdata.ResStatus(6) = 'House'; tdata.EmpStatus(7) = 'Freelancer'; tdata.CustIncome(8) = -1; disp(tdata(1:10,:))
CustAge ResStatus EmpStatus CustIncome TmWBank OtherCC AMBalance status
_______ ___________ ___________ __________ _______ _______ _________ ______
NaN Tenant Unknown 34000 44 Yes 119.8 1
48 <undefined> Unknown 44000 14 Yes 403.62 0
65 Home Owner <undefined> 48000 6 No 111.88 0
44 Other Unknown NaN 35 No 436.41 0
-100 Other Employed 46000 16 Yes 162.21 0
33 House Employed 36000 36 Yes 845.02 0
39 Tenant Freelancer 34000 40 Yes 756.26 1
24 Home Owner Employed -1 19 Yes 449.61 0
NaN Home Owner Employed 51000 11 Yes 519.46 1
52 Other Unknown 42000 12 Yes 1269.2 0
Use validatemodel for a compactCreditScorecard object with the validation data set (tdata).
[ValStats,ValTable] = validatemodel(csc,tdata,'Plot',{'CAP','ROC','KS'});

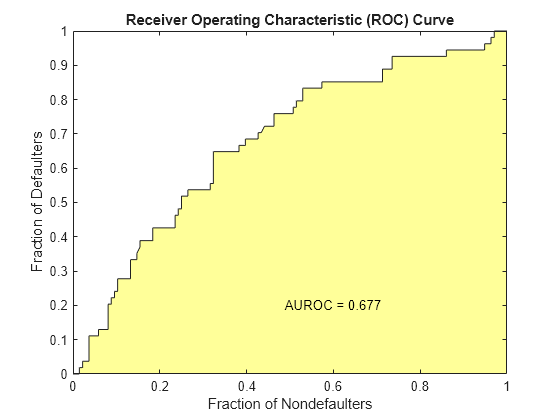

disp(ValStats)
Measure Value
________________________ _______
{'Accuracy Ratio' } 0.35376
{'Area under ROC curve'} 0.67688
{'KS statistic' } 0.32462
{'KS score' } 493.35
disp(ValTable(1:10,:))
Scores ProbDefault TrueBads FalseBads TrueGoods FalseGoods Sensitivity FalseAlarm PctObs
______ ___________ ________ _________ _________ __________ ___________ __________ _________
597.33 NaN 0 1 135 54 0 0.0073529 0.0052632
598.54 NaN 0 2 134 54 0 0.014706 0.010526
601.18 NaN 1 2 134 53 0.018519 0.014706 0.015789
637.3 NaN 1 3 133 53 0.018519 0.022059 0.021053
NaN 0.69421 2 3 133 52 0.037037 0.022059 0.026316
NaN 0.65394 2 4 132 52 0.037037 0.029412 0.031579
NaN 0.64441 2 5 131 52 0.037037 0.036765 0.036842
NaN 0.62799 3 5 131 51 0.055556 0.036765 0.042105
390.86 0.58964 4 5 131 50 0.074074 0.036765 0.047368
404.09 0.57902 6 5 131 48 0.11111 0.036765 0.057895
Input Arguments
Compact credit scorecard model, specified as a compactCreditScorecard object.
To create a compactCreditScorecard object, use
compactCreditScorecard or compact from
Financial Toolbox™.
Validation data, specified as a MATLAB® table, where each table row corresponds to individual
observations. The data must contain columns for each
of the predictors in the credit scorecard model. The columns of data can
be any one of the following data types:
Numeric
Logical
Cell array of character vectors
Character array
Categorical
String
String array
In addition, the table must contain a binary response
variable and the name of this column must match the name of the
ResponseVar property in the compactCreditScorecard object. (The
ResponseVar property in the compactCreditScorecard is copied from the
ResponseVar property of the original creditscorecard object.)
Note
If a different validation data set is provided using the
optional data input, observation weights for
the validation data must be included in a column whose name
matches WeightsVar from the original creditscorecard
object, otherwise unit weights are used for the validation data.
For more information, see Using validatemodel with Weights.
Data Types: table
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: csc =
validatemodel(csc,data,'Plot','CAP')
Type of plot, specified as the comma-separated pair consisting of
'Plot' and a character vector with one of the
following values:
'None'— No plot is displayed.'CAP'— Cumulative Accuracy Profile. Plots the fraction of borrowers up to score “s” against the fraction of defaulters up to score “s” ('PctObs'against'Sensitivity'columns ofToptional output argument). For details, see Cumulative Accuracy Profile (CAP).'ROC'— Receiver Operating Characteristic. Plots the fraction of non-defaulters up to score “s” against the fraction of defaulters up to score “s” ('FalseAlarm'against'Sensitivity'columns ofToptional output argument). For details, see Receiver Operating Characteristic (ROC).'KS'— Kolmogorov-Smirnov. Plots each score “s” against the fraction of defaulters up to score “s,” and also against the fraction of nondefaulters up to score “s” ('Scores'against both'Sensitivity'and'FalseAlarm'columns of the optional output argumentT). For details, see Kolmogorov-Smirnov statistic (KS).Tip
For the Kolmogorov-Smirnov statistic option, you can enter either
'KS'or'K-S'.
Data Types: char | cell
Output Arguments
Validation measures, returned as a
4-by-2 table. The first
column, 'Measure', contains the names of the
following measures:
Accuracy ratio (AR)
Area under the ROC curve (AUROC)
The KS statistic
KS score
The second column, 'Value', contains
the values corresponding to these measures.
Validation statistics data, returned as an
N-by-9 table of validation
statistics data, sorted by score from riskiest to safest.
N is equal to the total number of unique scores,
that is, scores without duplicates.
The table T contains the following nine columns, in
this order:
'Scores'— Scores sorted from riskiest to safest. The data in this row corresponds to all observations up to and including the score in this row.'ProbDefault'— Probability of default for observations in this row. For deciles, the average probability of default for all observations in the given decile is reported.'TrueBads'— Cumulative number of “bads” up to and including the corresponding score.'FalseBads'— Cumulative number of “goods” up to and including the corresponding score.'TrueGoods'— Cumulative number of “goods” above the corresponding score.'FalseGoods'— Cumulative number of “bads” above the corresponding score.'Sensitivity'— Fraction of defaulters (or the cumulative number of “bads” divided by total number of “bads”). This is the distribution of “bads” up to and including the corresponding score.'FalseAlarm'— Fraction of nondefaulters (or the cumulative number of “goods” divided by total number of “goods”). This is the distribution of “goods” up to and including the corresponding score.'PctObs'— Fraction of borrowers, or the cumulative number of observations, divided by total number of observations up to and including the corresponding score.
Note
When creating the creditscorecard object
with creditscorecard,
if the optional name-value pair argument
WeightsVar was used to specify
observation (sample) weights, then the T
table uses statistics, sums, and cumulative sums that are
weighted counts.
Figure handle to plotted measures, returned as a figure handle or
array of handles. When Plot is set to
'None', hf is an empty
array.
More About
CAP is generally a concave curve and is also known as the Gini curve, Power curve, or Lorenz curve.
The scores of given observations are sorted from riskiest to safest. For a
given fraction M (0% to 100%) of the total borrowers, the
height of the CAP curve is the fraction of defaulters whose scores are less than
or equal to the maximum score of the fraction M. This
fraction of defaulters is also known as the “Sensitivity.”.
The area under the CAP curve, known as the AUCAP, is then compared to that of the perfect or “ideal” model, leading to the definition of a summary index known as the accuracy ratio (AR) or the Gini coefficient:
where AR is the area between the CAP curve and the diagonal, and AP is the area between the perfect model and the diagonal. This represents a “random” model, where scores are assigned randomly and therefore the proportion of defaulters and nondefaulters is independent of the score. The perfect model is the model for which all defaulters are assigned the lowest scores, and therefore perfectly discriminates between defaulters and nondefaulters. Thus, the closer to unity AR is, the better the scoring model.
To find the receiver operating characteristic (ROC) curve, the proportion of defaulters up to a given score “s,” or “Sensitivity,” is computed.
This proportion is known as the true positive rate (TPR). Also, the proportion of nondefaulters up to score “s,“ or “False Alarm Rate,” is also computed. This proportion is also known as the false positive rate (FPR). The ROC curve is the plot of the “Sensitivity” vs. the “False Alarm Rate.” Computing the ROC curve is similar to computing the equivalent of a confusion matrix at each score level.
Similar to the CAP, the ROC has a summary statistic known as the area under the ROC curve (AUROC). The closer to unity, the better the scoring model. The accuracy ratio (AR) is related to the area under the curve by the following formula:
The Kolmogorov-Smirnov (KS) plot, also known as the fish-eye graph, is a common statistic for measuring the predictive power of scorecards.
The KS plot shows the distribution of defaulters and the distribution of nondefaulters on the same plot. For the distribution of defaulters, each score “s” is plotted against the proportion of defaulters up to “s," or “Sensitivity." For the distribution of non-defaulters, each score “s” is plotted against the proportion of nondefaulters up to "s," or "False Alarm." The statistic of interest is called the KS statistic and is the maximum difference between these two distributions (“Sensitivity” minus “False Alarm”). The score at which this maximum is attained is also of interest.
If you provide observation weights, the
validatemodel function incorporates the observation
weights when calculating model validation statistics.
If you do not provide weights, the validation statistics are based on how many good and bad observations fall below a particular score. If you do provide weights, the weight (not the count) is accumulated for the good and the bad observations that fall below a particular score.
When you define observation weights using the optional
WeightsVar name-value pair argument when creating a
creditscorecard object, the
weights stored in the WeightsVar column are used when
validating the model on the training data. When a different validation data set
is provided using the optional data input, observation
weights for the validation data must be included in a column whose name matches
WeightsVar. Otherwise, the unit weights are used for the
validation data set.
The observation weights of the training data affect not only the validation statistics but also the credit scorecard scores themselves. For more information, see Using fitmodel with Weights and Credit Scorecard Modeling Using Observation Weights.
References
[1] “Basel Committee on Banking Supervision: Studies on the Validation of Internal Rating Systems.” Working Paper No. 14, February 2005.
[2] Refaat, M. Credit Risk Scorecards: Development and Implementation Using SAS. lulu.com, 2011.
[3] Loeffler, G. and P. N. Posch. Credit Risk Modeling Using Excel and VBA. Wiley Finance, 2007.
Version History
Introduced in R2019b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)