derivative
Time derivative of manipulator model states
Syntax
Description
stateDot = derivative(taskMotionModel,state,refPose,refVel)
stateDot = derivative(jointMotionModel,state,cmds)
stateDot = derivative(jointMotionModel,state,cmds,fExt)
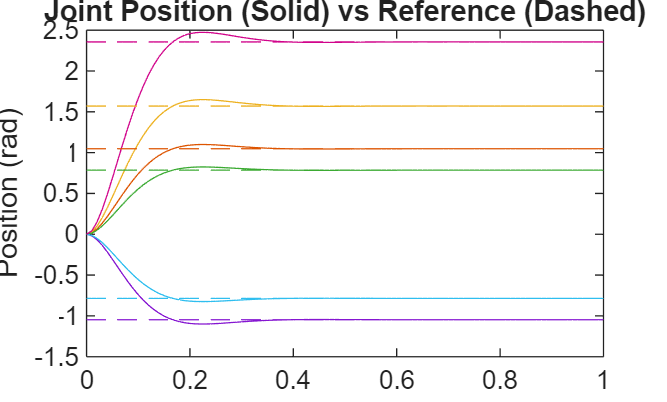
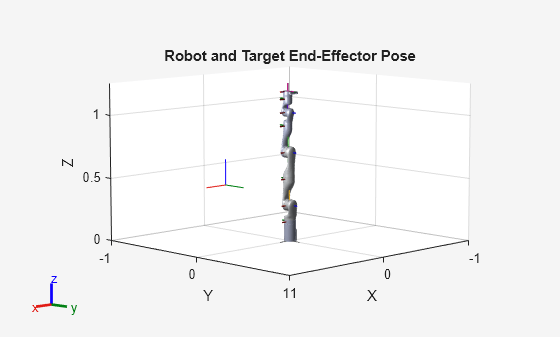
Examples
Input Arguments
Output Arguments
Extended Capabilities
Version History
Introduced in R2019b