Build Tunable Control System Model with Uncertain Parameters
This example shows how to construct a generalized state-space (genss) model of a control system that has both tunable and uncertain parameters. You can use systune to tune the tunable parameters of such a model to achieve performance that is robust against the uncertainty in the system.
For this example, the plant is a mass-spring-damper system. The input is the applied force, F, and the output is x, the position of the mass.

In this system, the mass m, the damping constant c, and the spring constant k all have some uncertainty. Use uncertain ureal parameters to represent these quantities in terms of their nominal or most probable value and a range of uncertainty around that value.
um = ureal('m',3,'Percentage',40); uc = ureal('c',1,'Percentage',20); uk = ureal('k',2,'Percentage',30);
The transfer function of a mass-spring-damper system is a second-order function given by:
Create this transfer function in MATLAB® using the uncertain parameters and the tf command. The result is an uncertain state-space (uss) model.
G = tf(1,[um uc uk])
Uncertain continuous-time state-space model with 1 outputs, 1 inputs, 2 states. The model uncertainty consists of the following blocks: c: Uncertain real, nominal = 1, variability = [-20,20]%, 1 occurrences k: Uncertain real, nominal = 2, variability = [-30,30]%, 1 occurrences m: Uncertain real, nominal = 3, variability = [-40,40]%, 1 occurrences Model Properties Type "G.NominalValue" to see the nominal value and "G.Uncertainty" to interact with the uncertain elements.
Suppose you want to control this system with a PID controller, and that your design requirements include monitoring the response to noise at the plant input. Build a model of the following control system.

Use a tunable PID controller, and insert an analysis point to provide access to the disturbance input.
C0 = tunablePID('C','PID'); d = AnalysisPoint('d');
Connect all the components to create the control system model.
T0 = feedback(G*d*C0,1)
Generalized continuous-time state-space model with 1 outputs, 1 inputs, 3 states, and the following blocks: C: Tunable PID controller, 1 occurrences. c: Uncertain real, nominal = 1, variability = [-20,20]%, 1 occurrences d: Analysis point, 1 channels, 1 occurrences. k: Uncertain real, nominal = 2, variability = [-30,30]%, 1 occurrences m: Uncertain real, nominal = 3, variability = [-40,40]%, 1 occurrences Model Properties Type "ss(T0)" to see the current value and "T0.Blocks" to interact with the blocks.
T0.InputName = 'r'; T0.OutputName = 'x';
T0 is a generalized state-space (genss) model that has both tunable and uncertain blocks. In general, you can use feedback and other model interconnection commands, such as connect, to build up models of more complex tunable and uncertain control systems from fixed-value LTI components, uncertain components, and tunable components.
When you plot system responses of a genss model that is both tunable and uncertain, the plot displays multiple responses computed at random values of the uncertain components. This sampling provides a general sense of the range of possible responses. All plots use the current value of the tunable components.
bodeplot(T0)
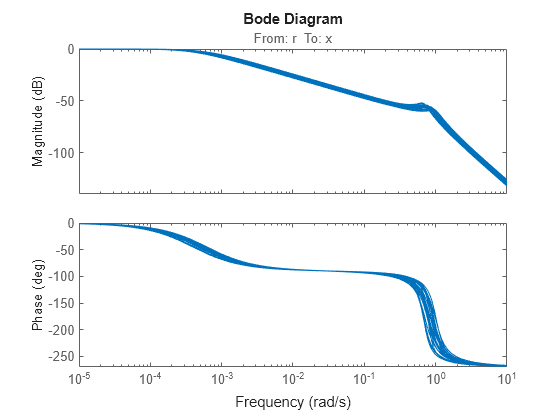
When you extract responses from a tunable and uncertain genss model, the responses also contain both tunable and uncertain blocks. For example, examine the loop transfer function at the disturbance input.
S0 = getLoopTransfer(T0,'d')Generalized continuous-time state-space model with 1 outputs, 1 inputs, 3 states, and the following blocks: C: Tunable PID controller, 1 occurrences. c: Uncertain real, nominal = 1, variability = [-20,20]%, 1 occurrences d: Analysis point, 1 channels, 1 occurrences. k: Uncertain real, nominal = 2, variability = [-30,30]%, 1 occurrences m: Uncertain real, nominal = 3, variability = [-40,40]%, 1 occurrences Model Properties Type "ss(S0)" to see the current value and "S0.Blocks" to interact with the blocks.
bodeplot(S0)
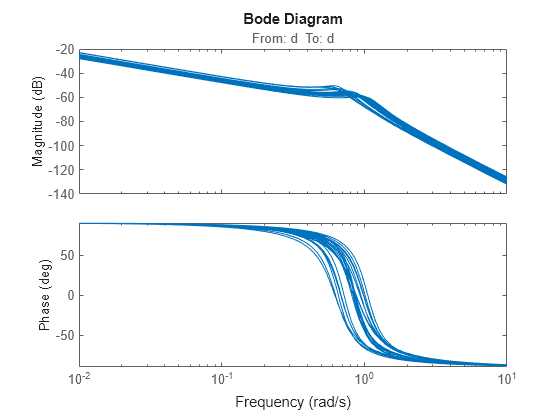
You can now create tuning goals and use systune to tune the PID controller coefficients of T0. When you do so, systune automatically tunes the coefficients to maximize performance over the full range of uncertainty.
See Also
ureal | genss | AnalysisPoint | connect