ultidyn

Uncertain linear time-invariant dynamics

Description

ultidyn objects represent uncertain linear time-invariant dynamics whose only known attributes are bounds on their frequency response. Combine ultidyn objects with other dynamic system models and uncertain elements to model systems with uncertain dynamics, represented by uss or genss models.

Creation

Syntax

H = ultidyn(name,iosize)

H = ultidyn(name,iosize,Name,Value)

Description

H = ultidyn(name,iosize) creates a ultidyn object modeling uncertain dynamics with a gain bound of 1 and output and input dimensions determined by iosize.

H = ultidyn(name,iosize,Name,Value) sets properties using one or more name-value arguments. For example, to set the gain bound to 0.1, set "Bound" to 0.1.

Input Arguments

iosize — Output and input dimensions

1 (default) | scalar | vector of form [Ny Nu]

Output and input dimensions of the uncertain dynamics, specified as a scalar value or a vector of the form [Ny Nu], where Ny is the number of outputs and Nu is the number of inputs. If you specify a scalar value N, then H has N outputs and inputs.

Properties

Type — Form in which to express bound on frequency response

'GainBounded' (default) | 'PositiveReal'

Form in which to express bound on the frequency response of the uncertain dynamics, specified as either 'GainBounded' or 'PositiveReal'. This value determines the meaning of the Bound property as follows:

• 'GainBounded' — The limit on the frequency response is expressed as an upper bound on the absolute gain, such that abs(H) <= H.Bound (for SISO dynamics) or hinfnorm(H) <= H.Bound (for MIMO dynamics) at all frequencies.

• 'PositiveReal' — The limit on the frequency response is expressed as a lower bound on the real part, such that Real(H) >= H.Bound (for SISO dynamics) or H + H' >= 2*H.Bound (for MIMO dynamics) at all frequencies.

Bound — Bound on frequency response

scalar

Bound on frequency response, specified as a scalar value. The meaning of this value depends on the value of the Type property, as described in description of that property. The default value also depends on how you set the Type property on object creation.

• If you do not specify Type or if you set Type = 'GainBounded' on object creation, then the default value is Bound = 1, meaning that the maximum absolute gain of the uncertain dynamics is 1 at all frequencies.

• If you set Type = 'PositiveReal' on object creation, then the default value is Bound = 0, meaning that the real part of the frequency response is greater than or equal to 0 at all frequencies.

SampleStateDimension — Number of states in random samples

3 (default) | positive integer

Number of states in random samples of the block, specified as an integer. Some analysis commands such as usample and bode take random samples of uncertain dynamics. This property determines the number of states in the samples. For more information about how sampling of dynamic uncertainty works, see Generate Samples of Uncertain Systems.

SampleMaxFrequency — Maximum frequency of random samples

Inf (default) | positive scalar

Maximum frequency of random samples, specified as a positive scalar value. Randomly sampled uncertain dynamics are no faster than the specified value.

NominalValue — Nominal value

ss model

This property is read-only.

Nominal value, specified as a state-space model with the output and input dimensions specified by iosize. The nominal value of a ultidyn block is always 0 regardless of the uncertain dynamics the block represents.

AutoSimplify — Block simplification level

'basic' (default) | 'full' | 'off'

Block simplification level, specified as 'basic', 'full', or 'off'. In general, when you combine uncertain elements to create uncertain state-space models, the software automatically applies techniques to eliminate redundant copies of the uncertain elements. (See simplify.) Use this property to specify the simplification to apply when you use model arithmetic or interconnection techniques with the uncertain block.

• 'basic' — Apply the elementary simplification method after each arithmetical or interconnection operation.

• 'full' — Apply techniques similar to model reduction.

• 'off' — Perform no simplification.

Name — Name of uncertain element

string | character vector

Name of uncertain element, specified as a string or character vector and stored as a character vector. When you create an uncertain state-space (uss or genss) model using uncertain control design blocks, the software tracks the blocks using the name you specify in this property, not the variable name in the MATLAB^® workspace. For example, if you create a ultidyn block using H = ultidyn("Delta",2), and combine the block with a numeric LTI model, the Blocks property of the resulting uss model lists the uncertain control design block Delta.

InputName — Names of input channels

{''} (default) | character vector | cell array of character vectors | string | string array

Names of input channels, specified as:

• A character vector or string — For single-input models

• A cell array of character vectors or a string array — For models with two or more inputs

• '' — For inputs without specified names

You can use automatic vector expansion to assign input names for multi-input models. For example, if sys is a two-input model, you can specify InputName as follows.

sys.InputName = 'controls';

The input names automatically expand to {'controls(1)';'controls(2)'}.

You can use the shorthand notation u to refer to the InputName property. For example, sys.u is equivalent to sys.InputName.

Input channel names have several uses, including:

• Identifying channels on model display and plots

• Extracting subsystems of MIMO systems

• Specifying connection points when interconnecting models

If you specify InputName using a string or string array, such as "voltage", the input name is stored as a character vector, 'voltage'.

InputUnit — Units of input signals

{''} (default) | character vector | cell array of character vectors | string | string array

Units of input signals, specified as:

• A character vector or string — For single-input models

• A cell array of character vectors or string array — For models with two or more inputs

• '' — For inputs without specified units

Use InputUnit to keep track of the units each input signal is expressed in. InputUnit has no effect on system behavior.

If you specify InputUnit using a string, such as "voltage", the input units are stored as a character vector, 'voltage'.

Example: 'voltage'

Example: {'voltage','rpm'}

InputGroup — Input channel groups

structure with no fields (default) | structure

Input channel groups, specified as a structure where the fields are the group names and the values are the indices of the input channels belonging to the corresponding group. When you use InputGroup to assign the input channels of MIMO systems to groups, you can refer to each group by name when you need to access it. For example, suppose you have a five-input model sys, where the first three inputs are control inputs and the remaining two inputs represent noise. Assign the control and noise inputs of sys to separate groups.

sys.InputGroup.controls = [1:3];
sys.InputGroup.noise = [4 5];

Use the group name to extract the subsystem from the control inputs to all outputs.

sys(:,'controls')

Example: struct('controls',[1:3],'noise',[4 5])

OutputName — Names of output channels

{''} (default) | character vector | cell array of character vectors or strings | string | string array

Names of output channels, specified as:

• A character vector or string— For single-output models

• A cell array of character vectors or string array — For models with two or more outputs

• '' — For outputs without specified names

You can use automatic vector expansion to assign output names for multi-output models. For example, if sys is a two-output model, you can specify OutputName as follows.

sys.OutputName = 'measurements';

The output names automatically expand to {'measurements(1)';'measurements(2)'}.

You can use the shorthand notation y to refer to the OutputName property. For example, sys.y is equivalent to sys.OutputName.

Output channel names have several uses, including:

• Identifying channels on model display and plots

• Extracting subsystems of MIMO systems

• Specifying connection points when interconnecting models

If you specify OutputName using a string, such as "rpm", the output name is stored as a character vector, 'rpm'.

OutputUnit — Units of output signals

{''} (default) | character vector | cell array of character vectors | string | string array

Units of output signals, specified as:

• A character vector or string — For single-output models

• A cell array of character vectors or string array — For models with two or more outputs

• '' — For outputs without specified units

Use OutputUnit to keep track of the units each output signal is expressed in. OutputUnit has no effect on system behavior.

If you specify OutputUnit using a string, such as "voltage", the output units are stored as a character vector, 'voltage'.

Example: 'voltage'

Example: {'voltage','rpm'}

OutputGroup — Output channel groups

structure with no fields (default) | structure

Output channel groups, specified as a structure where the fields are the group names and the values are the indices of the output channels belonging to the corresponding group. When you use OutputGroup to assign the output channels of MIMO systems to groups, you can refer to each group by name when you need to access it. For example, suppose you have a four-output model sys, where the second output is a temperature, and the rest are state measurements. Assign these outputs to separate groups.

sys.OutputGroup.temperature = [2];
sys.OutputGroup.measurements = [1 3 4];

Use the group name to extract the subsystem from all inputs to the measurement outputs.

sys('measurements',:)

Example: struct('temperature',[2],'measurement',[1 3 4])

Notes — Text notes about model

[0×1 string] (default) | string | character vector | cell array of character vectors or strings | string array

Text notes about the model, specified as a string or character vector. The property stores whichever of these two data types you provide. For instance, suppose that sys1 and sys2 are dynamic system models. You can set their Notes properties to a string and a character vector, respectively.

sys1.Notes = "sys1 has a string.";
sys2.Notes = 'sys2 has a character vector.';
sys1.Notes
sys2.Notes

ans = 

    "sys1 has a string."


ans =

    'sys2 has a character vector.'

You can also specify Notes as string array or a cell array of character vectors or strings.

UserData — Data associated with model

[] (default) | any data type

Data of any kind that you want to associate and store with the model, specified as any MATLAB data type.

Ts — Sample time

0 (default) | –1 | positive scalar

Sample time, specified as:

• 0 — For continuous-time models.

• Positive scalar value — For discrete-time models. Specify the sample time in the units given in the TimeUnit property of the model.

• –1 — For discrete-time models with unspecified sample time.

Changing this property does not discretize or resample the model.

TimeUnit — Model time units

'seconds' (default) | 'minutes' | 'milliseconds' | ...

Model time units, specified as:

• 'nanoseconds'

• 'microseconds'

• 'milliseconds'

• 'seconds'

• 'minutes'

• 'hours'

• 'days'

• 'weeks'

• 'months'

• 'years'

If you specify TimeUnit using a string, such as "hours", the time units are stored as a character vector, 'hours'.

Model properties such as sample time Ts, InputDelay, OutputDelay, and other time delays are expressed in the units specified by TimeUnit. Changing this property has no effect on other properties, and therefore changes the overall system behavior. Use to convert between time units without modifying system behavior.

Object Functions

Many functions that work on numeric LTI models also work on uncertain control design blocks such as ultidyn. These include model interconnection functions such as connect and feedback, and linear analysis functions such as bode and stepinfo. Some functions that generate plots, such as bode and step, plot random samples of the uncertain model to give you a sense of the distribution of uncertain dynamics. When you use these commands to return data, however, they operate on the nominal value of the system only. The following lists contain a representative subset of the functions you can use with ultidyn models.

Model Interconnection

feedback	Feedback connection of multiple models
connect	Block diagram interconnections of dynamic systems
series	Series connection of two models
parallel	Parallel connection of two models

Robustness and Worst-Case Analysis

usample	Generate random samples of uncertain model or element
usubs	Substitute given values for uncertain elements of uncertain objects

Linear Analysis

step	Step response of dynamic system
bode	Bode frequency response of dynamic system
nyquist	Nyquist response of dynamic system

Examples

Frequency-Dependent Uncertain Dynamics

To model frequency-dependent uncertainty levels, create a ultidyn object and multiply it by a suitable shaping filter. For instance, suppose that you know your system dynamics fairly well at low frequencies, and do not want to introduce uncertainty in that regime, but you have less understanding of the high-frequency dynamis. Create an uncertain dynamic system model representing an uncertainty with gain of 0.1 at low frequencies and gain of 10 at high frequencies.

First, create a SISO ultidyn block with gain less than 1 at all frequencies.

H = ultidyn("H",1)

Uncertain LTI dynamics "H" with 1 outputs, 1 inputs, and gain less than 1.

Next, create a weighting function with the gain profile you want, starting a 0.1 and increasing to 10.

W = tf([1 .1],[.1 1]);

Multiply H by the weighting function to create the desired dynamic uncertainty. Examine random samples of the resulting uncertain model to confirm that the gain of the uncertain dynamics has the desired frequency-dependent bound.

Delta = W*H;
bodemag(Delta)

You can combine Delta with other models to introduce the dynamic uncertainty to your system. For instance, suppose you can model your system with a state-space model with the following nominal value.

A = [-5 10;-10 -5];
B = [1 0;0 1];
C = [1 10;-10 1];
D = 0;
Pnom = ss(A,B,C,D);

Introduce Delta as an additive uncertainty.

Padd = Pnom + Delta;

Or, introduce Delta as multiplicative uncertainty on the input to Pnom.

Pmult = Pnom*(1+Delta);

Both Padd and Pmult are uss models with one uncertain block, the ultidyn block H.

MIMO Uncertain Dynamics

Create a ultidyn object with internal name 'H', norm bounded by 7, with three inputs and two outputs.

H = ultidyn('H',[2 3],'Bound',7) 

Uncertain LTI dynamics "H" with 2 outputs, 3 inputs, and gain less than 7.

Typically, when you use uncertain dynamics, you apply a weighting function to emphasize the uncertain contribution in a certain bandwidth. For instance, suppose that the behavior of your system is modestly uncertain (say 10%) at low frequencies, while the high-frequency behavior beyond 20 rad/s is not accurately modeled. Use makeweight to create a shaping filter that captures this behavior.

W = makeweight(.1,20,50);
bodemag(W)

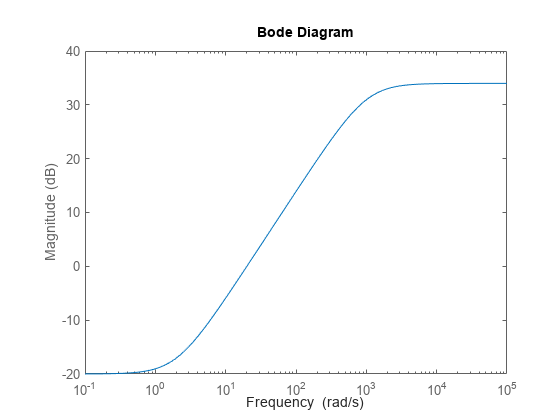
Apply the weighting filter at the block outputs. Examine samples of the unmodeled dynamics.

Hw = blkdiag(W,W)*H;
bodemag(Hw)

Nyquist Plot of Uncertain Dynamics

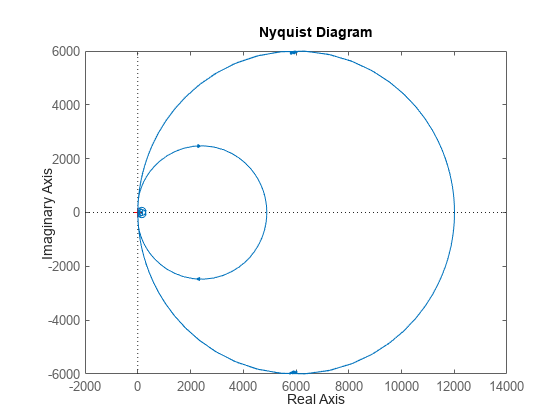
Create a scalar ultidyn object with an internal name 'B', whose frequency response has a real part greater than 2.5.

B = ultidyn('B',[1 1],'Type','PositiveReal','Bound',2.5)

Uncertain LTI dynamics "B" with 1 outputs, 1 inputs, and positive real bound of 2.5.

Change the SampleStateDimension to 5, and plot the Nyquist plot of 30 random samples.

B.SampleStateDimension = 5; 
nyquist(usample(B,30))

Version History

Introduced before R2006a

R2020a: Default value of SampleStateDimension property changed

The default value of the SampleStateDimension property is now 3. Prior to R2020a, the default value was 1.

SampleStateDimension sets the number of states in random samples of uncertain dynamics taken with analysis commands such as usample and bode. With SampleStateDimension = 1, all Nyquist plots of sampled dynamics touch the gain bound at either (–1,0) (frequency = 0) or (1,0) (frequency = Inf). Higher SampleStateDimension yields points of contact at other frequencies, meaning better coverage of worst-case possibilities. (The odds of hitting a worst-case value by random sampling is still very low. You can use sampling to get a rough idea of the effects of uncertainty, but for rigorous worst-case analysis, use commands such as wcgain and wcdiskmargin.) For an example of the effect of SampleStateDimension, see Generate Samples of Uncertain Systems.

If you have code that relies on the default value of SampleStateDimension being 1, update your code to explicitly set the property.