ctffilt

Cascaded transfer function filtering

Since R2024b

Syntax

y = ctffilt(B,A,x)

y = ctffilt({B,A,g},x)

[y,zf] = ctffilt(___,zi)

[___] = ctffilt(___,Dimension=dim)

Description

y = ctffilt(B,A,x) filters the input data x using Cascaded Transfer Functions (CTF) defined by the numerator and denominator coefficients B and A, respectively.

y = ctffilt({B,A,g},x) includes the scalar values g when filtering the input data, x.

[y,zf] = ctffilt(___,zi) uses initial conditions zi for the filter states. The function also returns the final conditions of the filter states zf.

[___] = ctffilt(___,Dimension=dim) acts along dimension dim. For example, if x is a matrix, then ctffilt(B,A,x,zi,Dimension=2) returns the filtered data for each row.

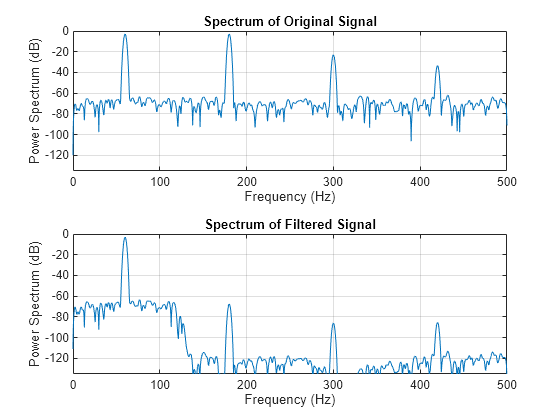
Examples

Two-Section Digital Filter

Specify a two-section digital filter with a transfer function $\mathit{H}\left(\mathit{z}\right)$. Plot the filter response.

$$\mathit{H}\left(\mathit{z}\right)=\left(0.1607+0.2414{\mathit{z}}^{-1}+0.4689{\mathit{z}}^{-2}\right)\times \frac{0.1607+0.0828{\mathit{z}}^{-1}+0.0551{\mathit{z}}^{-2}}{1-1.1940{\mathit{z}}^{-1}+0.4360{\mathit{z}}^{-2}}$$

B = [0.1607    0.2414    0.4689
     0.1607    0.0828    0.0551];
A = [     1         0         0;
          1   -1.1940    0.4360];
freqz(B,A,1024,"ctf")

Filter a signal consisting of two sinusoidal waveforms with frequencies of 0.1 Hz and 0.45 Hz, sampled every half second over a duration of one minute. The amplitude of the 0.45 Hz waveform is 0.3 times the amplitude of the 0.1 Hz waveform.

t = (0:0.5:60)';
s = sin(2*pi*0.1*t)+0.3*sin(2*pi*0.45*t);

x = timetable(seconds(t),s);

y = ctffilt(B,A,x);

Compare the input and output signals in the time domain. Because the magnitude of the filter response at 0.1 Hz is 0 dB, the amplitude of the output signal y is as high as the amplitude of the 0.1 Hz waveform from the input signal x.

tiledlayout flow
nexttile
plot(x,"s")
title("Input x")
nexttile
plot(y,"s")
title("Output y")

Remove Signal Harmonics Using Multisection Filter

Generate a sinusoidal signal with an amplitude of 1 V and a frequency of 60 Hz, and add third-, fifth-, and seventh-order harmonics. The harmonic amplitudes are 1 V, 0.1 V, and 0.03 V, respectively. Sample the signal for 1 second at a sample rate of 1000 Hz.

rng default
Fs = 1000;
a = [1 1 0.1 0.03];
f = 60*[1 3 5 7];
t = (0:1/Fs:1)';

x = cos(2*pi*f.*t)*a' + 0.005*randn(size(t));

Remove the third- and higher-order harmonic components from the mixed signal using a multisection lowpass elliptic filter. The cutoff frequency of the filter is 120 Hz.

Fc = 120;
wc = Fc/(Fs/2);
[num,den] = ellip(8,0.1,50,wc,"ctf");

y = ctffilt(num,den,x);

Plot the power spectrum for the original and filtered signals. The second plot shows that the power of the filtered signal decreases significantly at frequencies above 120 Hz.

tiledlayout flow
nexttile
pspectrum(x,Fs)
title("Spectrum of Original Signal")
ylim([-135 0])
nexttile
pspectrum(y,Fs)
title("Spectrum of Filtered Signal")
ylim([-135 0])

Successive Cascaded Bandpass Filtering

Design a fifth-order Butterworth bandpass filter represented as a cascade of fourth-order sections. The cutoff edge frequencies of the filter are 90 Hz and 150 Hz. The sample rate is 10 kHz.

Fs = 10000;
Wn  = [90 150]/(Fs/2);
[B,A] = butter(5,Wn,"bandpass","ctf")

B = 3×5

    0.0013    0.0026    0.0013         0         0
    0.0013    0.0026         0   -0.0026   -0.0013
    0.0013   -0.0052    0.0079   -0.0052    0.0013

A = 3×5

    1.0000   -1.9578    0.9630         0         0
    1.0000   -3.9289    5.7991   -3.8109    0.9408
    1.0000   -3.9650    5.9071   -3.9191    0.9770

The number of rows and columns in B and A indicate that the resulting filter has three fourth-order sections. There is one more column than the degree of the section polynomials to include the coefficient of the ${\mathit{z}}^0$ term.

Since the order of each filter section is four, the initial condition states in each section must have four elements. You can specify a four-element vector to set up the same initial condition states for the three filter sections, or a 12-element vector to set up these states explicitly for each filter section.

Specify the initial condition states for all filter sections as zeros.

L = size(B,1);
r = max(size(B,2),size(A,2))-1;
numStates = L*r;
zi = zeros(1,numStates);

Perform successive filtering on a noisy sinusoid using the bandpass filter.

1. Partition the signal into frames. Each frame has 50 samples.

2. Filter each frame of the signal using the initial condition states and compute the final condition states. Use these final condition states as the initial condition states for the next frame.

3. Repeat the previous step until the entire signal is filtered.

rng default
t = single(0:1/Fs:1-1/Fs);
x = sin(2*pi*10*t) + 0.5*sin(2*pi*100*t) + 0.1*randn(size(t));
% Signal framing:
fl = 50; % Frame length
xFramed = framesig(x,fl);
% Successive filtering across frames:
ySuccessive = [];
zf = zi;
for nFrame = 1:size(xFramed,2)
    [yFrame,zf] = ctffilt(B,A,xFramed(:,nFrame)',zf);
    ySuccessive = [ySuccessive yFrame];
end

Filter the entire noisy signal in a single operation.

yDirect = ctffilt(B,A,x,zi);

Compare the noisy signal with the filtered signal for the first 0.25 seconds. Successive filtering across the signal frames yields the same result as filtering the entire signal once.

plot(t,x,t,ySuccessive,t,yDirect,"--")
legend(["Noisy" "Filtered" "Filtered"]'+" signal" ...
    + ["" " (Successive)" " (Direct)"]')
xlabel("Time (seconds)")
ylabel("Amplitude (volts)")
xlim([0 0.25])

Elliptic Filter Impulse Response

Design an eighth-order lowpass elliptic filter by specifying the sample rate ${\mathit{F}}_{\mathrm{s}}=8192$ Hz , cutoff frequency 2000 Hz, passband ripple 0.5 dB, and stopband attenuation 60 dB. Then, design an impulse signal with 400 samples.

% Filter design
Fs = 8192;
Wn = 2000/(Fs/2);
[num,den,sv] = ellip(8,0.5,60,Wn,"ctf");

% Impulse signal
Ns = 400;
x = [1;zeros(Ns-1,1)];

Derive the impulse response of the elliptic filter by filtering the impulse signal x and by computing the filter response.

% Filter impulse signal
h = ctffilt({num,den,sv},x);
% Compute filter impulse response
hImp = impz({num,den,sv},"ctf",Ns);

Compare the impulse responses. Both approaches yield the same result.

stem(h,"filled")
hold on
scatter(1:Ns,hImp)
hold off
xlabel("Sample Number")

Impulse and Step Responses of Multisection Filter

Design a three-section decimate-by-five cascaded integrator-comb (CIC) filter. Each section has a unit differential delay. Plot the frequency response of the cascaded transfer function.

$$\mathit{H}\left(\mathit{z}\right)={\left(\frac{1-{\mathit{z}}^{-\mathit{ND}}}{1-{\mathit{z}}^{-1}}\right)}^{\mathit{K}}={\left(\frac{1-{\mathit{z}}^{-5}}{1-{\mathit{z}}^{-1}}\right)}^3$$

N = 1; % Differential delay
D = 5; % Decimation factor
K = 3; % Number of sections
num = repmat([1 zeros(1,N*D-1) -1],K,1)

num = 3×6

     1     0     0     0     0    -1
     1     0     0     0     0    -1
     1     0     0     0     0    -1

den = repmat([1 -1],K,1)

den = 3×2

     1    -1
     1    -1
     1    -1

freqz(num,den,"ctf")

Compute the 100-sample impulse and step responses of the CIC filter. Use the Dimension input argument to compute the filter responses using a multichannel signal structure x.

Ns = 100;
xImpl = [1 zeros(1,Ns-1)];
xStep = ones(1,Ns);
x = [xImpl;xStep];

y = ctffilt(num,den,x,Dimension=2);

Downsample and plot the decimated filter responses. Normalize the responses with respect to their maxima.

yDec = downsample(y',D);
plot(yDec./max(yDec),"*-")
xlabel("Sample Number")
title("Decimated Filter Responses")
legend(["Impulse" "Step"])

Input Arguments

B,A — Cascaded transfer function (CTF) coefficients

scalars | vectors | matrices

Since R2024b

Cascaded transfer function (CTF) coefficients, specified as scalars, vectors, or matrices. B and A list the numerator and denominator coefficients of the cascaded transfer function, respectively.

B must be of size L-by-(m + 1) and A must be of size L-by-(n + 1), where:

• L represents the number of filter sections.

• m represents the order of the filter numerators.

• n represents the order of the filter denominators.

For more information about the cascaded transfer function format and coefficient matrices, see Specify Digital Filters in CTF Format.

Note

If any element of A(:,1) is not equal to 1, then ctffilt normalizes the filter coefficients by A(:,1). In this case, A(:,1) must be nonzero.

Data Types: double | single
Complex Number Support: Yes

g — Scale values

scalar | vector

Since R2024b

Scale values, specified as a real-valued scalar or as a real-valued vector with L + 1 elements, where L is the number of CTF sections. The scale values represent the distribution of the filter gain across sections of the cascaded filter representation.

The ctffilt function applies a gain to the filter sections using the scaleFilterSections function depending on how you specify g:

• Scalar — The function distributes the gain uniformly across all filter sections.

• Vector — The function applies the first L gain values to the corresponding filter sections and distributes the last gain value uniformly across all filter sections.

Data Types: double | single

x — Input signal data

vector | matrix | multidimensional array | timetable

Input signal data, specified as a vector, matrix, multidimensional array, or MATLAB^® timetable.

• If x is a vector, then ctffilt returns the filtered data y as a vector of the same size as x.

• If x is a matrix, then ctffilt acts along the first dimension and returns the filtered data y for each column.

• If x is a multidimensional array, then ctffilt acts along the first array dimension whose size is greater than 1.

• If x is a MATLAB timetable, x must be regular and can have either a single variable containing a vector or matrix or multiple variables each containing a vector.

Data Types: double | single
Complex Number Support: Yes

zi — Initial conditions for filter states

[] (default) | vector | matrix | multidimensional array

Initial conditions for filter states, specified as a vector, matrix, or multidimensional array. The ctffilt function assumes that the filter has a transposed direct form II structure and r states per section, where r = max(length(A),length(B))-1.

• If zi is a vector, you must specify its length as:

  • r — The function initializes the filter states using the same set of initial conditions across all filter sections.

  • L*r — The function initializes the filter states using a unique set of initial conditions in each filter section. For example, the function initializes the filter states in the lth section using the vector formed by the elements from indices (l-1)*r+1 to l*r.

• If zi is a matrix or multidimensional array, then the size of the leading dimension must be L*r, where L is the number of sections of the filter in the CTF format. The size of each remaining dimension must match the size of the corresponding dimension of x. For example, when you use ctffilt along the second dimension (Dimension=2) of a 3-by-4-by-5 array x, the array zi must be of the size L*r-by-3-by-5.

The default value [] initializes all filter delays to zero.

Data Types: double | single
Complex Number Support: Yes

dim — Dimension to operate along

positive integer scalar

Dimension to operate along, specified as a positive integer scalar. By default, the function operates along the first array dimension of x with size greater than 1.

Note

This argument is not supported for timetable inputs. If you specify x as timetable, ctffilt operates along the columns of variables in x.

Data Types: double | single | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

Output Arguments

y — Filtered signal data

vector | matrix | multidimensional array | timetable

Filtered signal data, returned as a vector, matrix, multidimensional array, or MATLAB timetable.

• The ctffilt function returns y such that it is the same size as x.

• If B, A, x, or zi is of type single, then ctffilt computes the filtering operation using single-precision arithmetic, and returns y as type single. Otherwise, ctffilt returns y as type double.

zf — Final conditions for filter states

vector | matrix | multidimensional array

Final conditions for filter states, returned as a vector, matrix, or multidimensional array. The function assumes that the filter has a transposed direct form II structure and r states per section, where r = max(size(A,2),size(B,2))-1.

• If x is a vector, then zf is a column vector of length L*r, where L is the number of sections of the filter in the CTF format. The function returns the filter states in the lth section in the vector formed by the elements from indices (l-1)*r+1 to l*r.

• If x is a matrix or multidimensional array, then zf is a matrix or multidimensional array of column vectors of length L*r. The size of each remaining dimension of zf matches the size of the corresponding dimension of x. For example, when you use ctffilt along the second dimension (Dimension = 2) of a 3-by-4-by-5 array x, the array zf is of the size L*r-by-3-by-5.

More About

Cascaded Transfer Functions

Partitioning an IIR digital filter into cascaded sections improves its numerical stability and reduces its susceptibility to coefficient quantization errors. The cascaded form of a transfer function H(z) in terms of the L transfer functions H₁(z), H₂(z), …, H_L(z) is

$$H(z)={\displaystyle \prod _{l=1}^L{H}_l(z)}=H_1(z)\times H_2(z)\times \cdots \times H_L(z).$$

Specify Digital Filters in CTF Format

You can specify digital filters in the CTF format for analysis, visualization, and signal filtering. Specify a filter by listing its coefficients B and A. You can also include the filter scaling gain across sections by specifying a scalar or vector g.

Filter Coefficients

When you specify the coefficients as L-row matrices,

$$B=\left[\begin{array}{cccc}{b}_{11}& b_{12}& \cdots & b_{1,m+1}\\ b_{21}& b_{22}& \cdots & b_{2,m+1}\\ ⋮& ⋮& \ddots & ⋮\\ b_{L1}& b_{L2}& \cdots & b_{L,m+1}\end{array}\right],A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1,n+1}\\ a_{21}& a_{22}& \cdots & a_{2,n+1}\\ ⋮& ⋮& \ddots & ⋮\\ a_{L1}& a_{L2}& \cdots & a_{L,n+1}\end{array}\right],$$

it is assumed that you have specified the filter as a sequence of L cascaded transfer functions, such that the full transfer function of the filter is

$$H\left(z\right)=\frac{b_{11}+b_{12}{z}^{-1}+\cdots +b_{1,m+1}{z}^{-m}}{a_{11}+a_{12}{z}^{-1}+\cdots +a_{1,n+1}{z}^{-n}}\times \frac{b_{21}+b_{22}{z}^{-1}+\cdots +b_{2,m+1}{z}^{-m}}{a_{21}+a_{22}{z}^{-1}+\cdots +a_{2,n+1}{z}^{-n}}\times \cdots \times \frac{b_{L1}+b_{L2}{z}^{-1}+\cdots +b_{L,m+1}{z}^{-m}}{a_{L1}+a_{L2}{z}^{-1}+\cdots +a_{L,n+1}{z}^{-n}},$$

where m ≥ 0 is the numerator order of the filter and n ≥ 0 is the denominator order.

• If you specify both B and A as vectors, it is assumed that the underlying system is a one-section IIR filter (L = 1), with B representing the numerator of the transfer function and A representing its denominator.

• If B is scalar, it is assumed that the filter is a cascade of all-pole IIR filters with each section having an overall system gain equal to B.

• If A is scalar, it is assumed that the filter is a cascade of FIR filters with each section having an overall system gain equal to 1/A.

Note

• To convert second-order section matrices to cascaded transfer functions, use the sos2ctf function.

• To convert a zero-pole-gain filter representation to cascaded transfer functions, use the zp2ctf function.

Coefficients and Gain

If you have an overall scaling gain or multiple scaling gains factored out from the coefficient values, you can specify the coefficients and gain as a cell array of the form {B,A,g}. Scaling filter sections is especially important when you work with fixed-point arithmetic to ensure that the output of each filter section has similar amplitude levels, which helps avoid inaccuracies in the filter response due to limited numeric precision.

The gain can be a scalar overall gain or a vector of section gains.

• If the gain is scalar, the value applies uniformly to all the cascade filter sections.

• If the gain is a vector, it must have one more element than the number of filter sections L in the cascade. Each of the first L scale values applies to the corresponding filter section, and the last value applies uniformly to all the cascade filter sections.

If you specify the coefficient matrices and gain vector as

$$B=\left[\begin{array}{cccc}{b}_{11}& b_{12}& \cdots & b_{1,m+1}\\ b_{21}& b_{22}& \cdots & b_{2,m+1}\\ ⋮& ⋮& \ddots & ⋮\\ b_{L1}& b_{L2}& \cdots & b_{L,m+1}\end{array}\right],A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1,n+1}\\ a_{21}& a_{22}& \cdots & a_{2,n+1}\\ ⋮& ⋮& \ddots & ⋮\\ a_{L1}& a_{L2}& \cdots & a_{L,n+1}\end{array}\right],g=\left[\begin{array}{ccccc}{g}_1& g_2& \cdots & g_L& g_{\text{S}}\end{array}\right],$$

it is assumed that the transfer function of the filter system is

$$H\left(z\right)=g_{\text{S}}\left(g_1\frac{b_{11}+b_{12}{z}^{-1}+\cdots +b_{1,m+1}{z}^{-m}}{a_{11}+a_{12}{z}^{-1}+\cdots +a_{1,n+1}{z}^{-n}}\times g_2\frac{b_{21}+b_{22}{z}^{-1}+\cdots +b_{2,m+1}{z}^{-m}}{a_{21}+a_{22}{z}^{-1}+\cdots +a_{2,n+1}{z}^{-n}}\times \cdots \times g_L\frac{b_{L1}+b_{L2}{z}^{-1}+\cdots +b_{L,m+1}{z}^{-m}}{a_{L1}+a_{L2}{z}^{-1}+\cdots +a_{L,n+1}{z}^{-n}}\right).$$

Tips

• You can obtain filters in CTF format, including the scaling gain. Use the outputs of digital IIR filter design functions, such as butter, cheby1, cheby2, and ellip. Specify the "ctf" filter-type argument in these functions and specify to return B, A, and g to get the scale values. (since R2024b)

Algorithms

The ctffilt function uses the transposed direct form II structure to implement the filter from the coefficients and gain in the cascaded transfer function format.

Assume that the filter has l sections with coefficients b_li and a_lj, derived from the matrices B,A in the CTF format, and the scale value(s) g. The values i – 1 and j – 1 denote the exponents of z of the numerator and denominator polynomials in the z-domain, respectively. The ctffilt function normalizes a_li and b_li to α_li and β_li, respectively, ensuring that α_l1 equals unity.

$$\begin{array}{l}{\beta }_{li}=\mathrm{sgn}(g_{\text{S}})|g_{\text{S}}{|}^{1/L}{g}_l\frac{b_{li}}{a_{l1}},i=1,2,\mathrm{...},m+1\\ {\alpha }_{lj}=\frac{a_{lj}}{a_{l1}},j=1,2,\mathrm{...},n+1\end{array}$$

When you specify g as a scalar, ctffilt assumes that g=g_S, and the term g_l does not apply in the normalization of the filter coefficients β_li.

If the orders of the polynomial numerators and denominators are given as m and n, respectively, the filter has r = max(m,n) states per section. These states are located at the outputs of each z^-1 delay block in the filter implementation diagram.

• When you specify zi as a vector with r elements, ctffilt initializes the filter states by setting ν_1k = ν_2k = … = ν_Lk = zi(k) for k = 1, 2, …, r.

• When you specify zi as a vector, matrix, or multidimensional array with L*r elements in its leading dimension, ctffilt initializes the filter states by setting ν_lk = zi((l-1)*r+k) for k = 1, 2, …, r and l = 1, 2, …, L.

For each sample of x across the first array dimension whose size is greater than 1 or across the dimension dim that you specify as Dimension=dim, the ctffilt function computes y by following the filter implementation based on the transposed direct form II structure, updates the filter states ν_lk, and repeats this operation until it finishes filtering the last sample of x.

• When you specify to return zf, ctffilt gathers the states ν_lk computed during the filtering of the last sample of x, and stores them in zf as zf((l-1)*r+k) = ν_lk, for k = 1, 2, …, r and l = 1, 2, …, L.

References

[1] Lyons, Richard G. Understanding Digital Signal Processing. Upper Saddle River, NJ: Prentice Hall, 2004.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

The ctffilt function supports GPU array input with these usage notes and limitations:

• The zi and zf arguments are not supported.

For more information, see Run MATLAB Functions in Thread-Based Environment.

Version History

Introduced in R2024b