Define Reaction Rates with Enzyme Kinetics

Use differential equations, mass action kinetics, or Michaelis-Menten kinetics to define enzyme reactions.

Simple Model for Single Substrate Catalyzed Reactions

A simple model for enzyme-catalyzed reactions starts a substrate S reversibly binding with an enzyme E. Some of the substrate in the substrate/enzyme complex is converted to product P with the release of the enzyme.

 $S + E ⇄_{k1r}^{k1} ES \overset{k2}{\to} E + P$ 
 $v1 = k1[S][E],   v1r = k1r[ES],   v2 = k2[ES]$

This simple model can be defined with

Differential rate equations. See Enzyme Reactions with Differential Rate Equations.
Reactions with mass action kinetics. See Enzyme Reactions with Mass Action Kinetics.
Reactions with Henri-Michaelis-Menten kinetics. See Enzyme Reactions with Irreversible Henri-Michaelis-Menten Kinetics.

Enzyme Reactions with Differential Rate Equations

The reactions for a single-substrate enzyme reaction mechanism (see Simple Model for Single Substrate Catalyzed Reactions) can be described with differential rate equations. You can enter the differential rate equations into the software as rate rules.

     reactions: none
 reaction rate: none
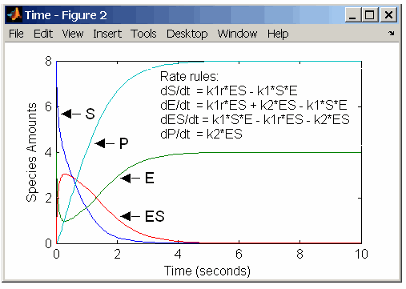
    rate rules: dS/dt  = k1r*ES - k1*S*E
                dE/dt  = k1r*ES + k2*ES - k1*S*E
                dES/dt = k1*S*E - k1r*ES - k2*ES
                dP/dt  = k2*ES
       species: S =  8   mole
                E =  4   mole
               ES =  0   mole
                P =  0   mole
    parameters:  k1 = 2   1/(mole*second)
                k1r = 1   1/second
                 k2 = 1.5 1/second

Remember that the rate rule dS/dt = f(x) is written in a SimBiology^® rate rule expression as S = f(x). For more information about rate rules see Rate Rules.

Alternatively, you could remove the rate rule for ES, add a new species Etotal for the total amount of enzyme, and add an algebraic rule 0 = Etotal - E - ES, where the initial amounts for Etotal and E are equal.

      reactions: none
  reaction rate: none
     rate rules: dS/dt = k1r*ES - k1*S*E
                 dE/dt = k1r*ES + k2*ES - k1*S*E
                 dP/dt = k2*ES
 algebraic rule: 0 = Etotal - E - ES
        species: S =  8   mole
                 E =  4   mole
                ES =  0   mole
                 P =  0   mole
            Etotal =  4   mole
     parameters: k1 = 2   1/(mole*second)
                k1r = 1   1/second
                 k2 = 1.5 1/second

Enzyme Reactions with Mass Action Kinetics

Determining the differential rate equations for the reactions in a model is a time-consuming process. A better way is to enter the reactions for a single substrate enzyme reaction mechanism directly into the software. The following example using models an enzyme catalyzed reaction with mass action kinetics. For a description of the reaction model, see Simple Model for Single Substrate Catalyzed Reactions.

     reaction: S + E -> ES
reaction rate: k1*S*E (binding)

     reaction: ES -> S + E 
reaction rate: k1r*ES (unbinding)

     reaction: ES -> E + P
reaction rate: k2*ES (transformation)
      species: S =  8   mole
               E =  4   mole
              ES =  0   mole
               P =  0   mole
   parameters: k1  = 2   1/(mole*second)
               k1r = 1   1/second
               k2  = 1.5 1/second

The results for a simulation using reactions are identical to the results from using differential rate equations.

Enzyme Reactions with Irreversible Henri-Michaelis-Menten Kinetics

Representing an enzyme-catalyzed reaction with mass action kinetics requires you to know the rate constants k1, k1r, and k2. However, these rate constants are rarely reported in the literature. It is more common to give the rate constants for Henri-Michaelis-Menten kinetics with the maximum velocity Vm=k2*E and the constant Km = (k1r + k2)/k1. The reaction rate for a single substrate enzyme reaction using Henri-Michaelis-Menten kinetics is given below. For information about the model, see Simple Model for Single Substrate Catalyzed Reactions.

$v = \frac{Vmax[S]}{Km + [S]}$

The following example models an enzyme catalyzed reaction using Henri-Michaelis-Menten kinetics with a single reaction and reaction rate equation. Enter the reaction defined below into the software and simulate.

     reaction: S -> P
reaction rate: Vmax*S/(Km + S)
      species:    S =  8    mole
                  P =  0    mole
   parameters: Vmax =  6    mole/second
                 Km =  1.25 mole

The results show a plot slightly different from the plot using mass action kinetics. The differences are due to assumptions made when deriving the Michaelis-Menten rate equation.