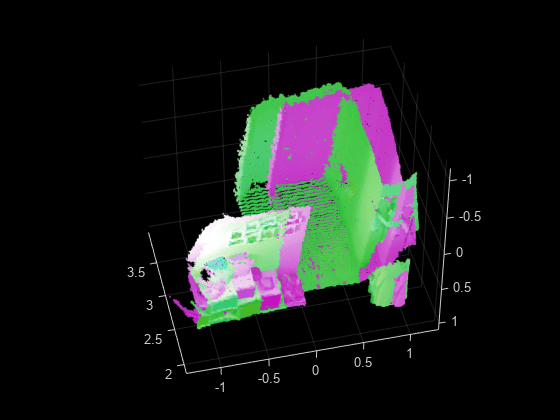
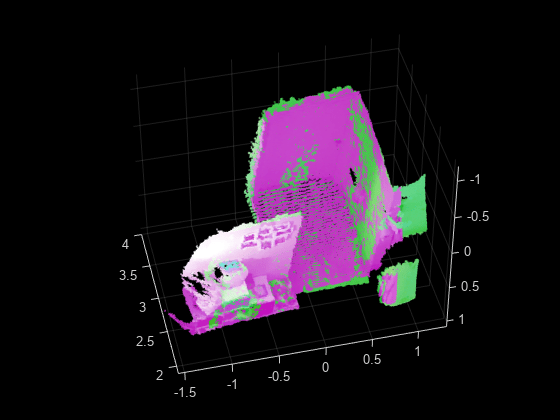
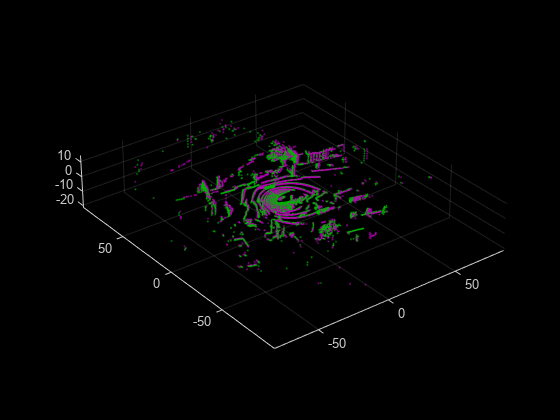
pcregisterndt
Register two point clouds using NDT algorithm
Syntax
Description
tform = pcregisterndt(moving,fixed,gridStep)gridStep.
The registration algorithm is based on the normal-distributions transform (NDT)
algorithm [1]
[2]. Best performance of
this iterative process requires adjusting properties for your data. To improve
accuracy and efficiency of registration, consider downsampling the moving point
cloud by using pcdownsample before using
pcregisterndt.
[___] = pcregisterndt(___,
specifies options using one or more name-value arguments in addition to any
combination of arguments from previous syntaxes. For example,
Name=Value)MaxIterations=20 stops the NDT algorithm after 20 iterations.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
References
[1] Biber, P., and W. Straßer. “The Normal Distributions Transform: A New Approach to Laser Scan Matching.” Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Las Vegas, NV. Vol. 3, November 2003, pp. 2743–2748.
[2] Magnusson, M. “The Three-Dimensional Normal-Distributions Transform — an Efficient Representation for Registration, Surface Analysis, and Loop Detection.” Ph.D. Thesis. Örebro University, Örebro, Sweden, 2013.
Extended Capabilities
Version History
Introduced in R2018aSee Also
Functions
pcregistercorr|pcregistericp|pcregistercpd|pctransform|pcshow|pcshowpair|pcdownsample|pcfitplane|pcdenoise|pcmerge