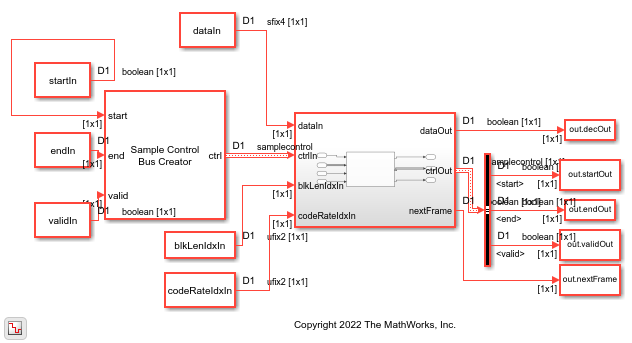
CCSDS LDPC Decoder

Decode LDPC code according to CCSDS standard

Since R2022b

• 

×

Libraries:
Wireless HDL Toolbox / Error Detection and Correction

Description

The CCSDS LPDC Decoder block implements a low-density parity-check (LDPC) decoder using a layered belief propagation algorithm with min-sum approximation for decoding LDPC codes according to the Consultative Committee for Space Data Systems (CCSDS) standard [1]. The block accepts log-likelihood ratio (LLR) values, a stream of control signals, a block length, and a code rate as inputs. The block outputs decoded bits, a stream of control signals, and a signal that indicates when the block is ready to accept new inputs.

The block supports scalar inputs and vector inputs of size 8. The block supports early termination to improve decoding performance and convergence speeds at high signal-to-noise ratio (SNR) conditions.

The block provides an architecture suitable for HDL code generation and hardware deployment. You can use this block in a CCSDS receiver for satellite communication.

Examples

Decode and Recover Message Using CCSDS LDPC Decoder

Decode and recover message from codeword using CCSDS LDPC Decoder.

Open Script

Ports

Input

data — LLR values

scalar | eight-element row vector

LLR values, specified as a scalar or an eight-element row vector.

For HDL code generation, specify this value in signed fixed-point format. The input word length must be an integer in the range [4, 16] and the fractional length must be in the range [0, 15].

Data Types: int8 | int16 | signed fixed point

ctrl — Control signals accompanying sample stream

samplecontrol bus

Control signals accompanying the sample stream, specified as a samplecontrol bus. The bus includes the start, end, and valid control signals, which indicate the boundaries of the frame and the validity of the samples.

• start — Indicates the start of the input frame

• end — Indicates the end of the input frame

• valid — Indicates that the data on the input data port is valid

For more details, see Sample Control Bus.

Data Types: bus

codeRateIdx — Code rate index

0 | 1 | 2

Code rate index, specified as 0, 1, or 2. You must specify this value in the fixdt(0,2,0) format. Each code rate index value represents a specific code rate, as this table shows.

codeRateIdx Value	Code Rate
0	1/2
1	2/3
2	4/5

Dependencies

To enable this port, set the Configuration type parameter to AR4JA LDPC.

Data Types: fixdt(0,2,0)

blkLenIdx — Block length index

0 | 1 | 2

Block length index, specified as 0, 1, or 2. You must specify this value in the fixdt(0,2,0) format.

The block length varies with the specified block length index. The input block length must be a multiple of 8. This table shows the block length index values and their corresponding block lengths.

blkLenIdx Value	Block Length
0	1024
1	4096
2	16384

Dependencies

To enable this port, set the Configuration type parameter to AR4JA LDPC.

Data Types: fixdt(0,2,0)

iter — Number of iterations

integer in the range [1, 63]

Number of iterations, specified as an unsigned integer in the range [1, 63].

If you specify an iter value greater than 63 or less than 1, the block overrides your specification and sets the iter value to 8 before it performs decoding.

Dependencies

To enable this port, set the Decoding termination criteria parameter to Max and the Source for number of iterations parameter to Input port.

Data Types: uint8

Output

data — Decoded bits

scalar | eight-element row vector

Decoded bits, returned as a Boolean scalar or an eight-element row vector of Boolean values.

Data Types: Boolean

ctrl — Control signals accompanying sample stream

samplecontrol bus

Control signals accompanying the sample stream, returned as a samplecontrol bus. The bus includes the start, end, and valid control signals, which indicate the boundaries of the frame and the validity of the samples.

• start — Indicates the start of the output frame

• end — Indicates the end of the output frame

• valid — Indicates that the data on the output data port is valid

For more details, see Sample Control Bus.

Data Types: bus

nextFrame — Block ready indicator

0 | 1

Block ready indicator, returned as a Boolean scalar.

The block sets this signal to 1 when the block is ready to accept the start of the next frame. If the block receives an input ctrl.start signal while nextFrame is 0, the block discards the frame in progress and begins processing the new data.

Data Types: Boolean

actIter — Actual number of iterations

positive scalar

Actual number of iterations the block takes to decode the output, returned as a positive scalar.

Dependencies

To enable this port, set the Decoding termination criteria parameter to Early.

Data Types: uint8

parityCheck — Parity check status indicator

0 | 1

Parity check status indicator, returned as a Boolean scalar. The port indicates the status of the parity check after the decoding operation.

• 0 — Indicates that the parity check failed

• 1 — Indicates that the parity check passed

Dependencies

To enable this port, select the Enable parity check output port parameter.

Data Types: Boolean

Parameters

Configuration type — Type of configuration

(8160,7136) LDPC (default) | AR4JA LDPC

Select the configuration type. For more information about the supported configurations, see [1].

Decoding termination criteria — Termination criteria

Max (default) | Early

Select the decoding termination criteria.

• Max — Terminate decoding when the block reaches the number of iterations specified in the block mask or the iter input port.

• Early — Terminate decoding when the block completes all of the parity checks or when the block reaches the maximum number of iterations specified in the block mask.

Source for number of iterations — Source selection for number of iterations

Property (default) | Input port

Select the source for specifying the number of iterations.

You can set the number of iterations by using an input port or a parameter.

• Property — Select this option to enable the Number of iterations parameter.

• Input port — Select this option to enable the iter port.

Number of iterations — Number of decoding iterations

8 (default) | integer in the range [1, 63]

Specify the number of decoding iterations.

Dependencies

To enable this parameter, set the Decoding termination criteria parameter to Max and the Source for number of iterations parameter to Property.

Maximum number of iterations — Maximum number of decoding iterations

8 (default) | integer in the range [1, 63]

Specify the maximum number of decoding iterations.

Dependencies

To enable this parameter, set the Decoding termination criteria parameter to Early and set the Source for number of iterations parameter to Property.

Enable parity check output port — Parity check status

off (default) | on

Select this parameter to enable the parityCheck output port. Use this output port to view the status of the parity check.

Algorithms

This figure shows the architecture block diagram of the CCSDS LDPC Decoder block. The Controller block controls the layer and iteration count of the decoding process. The Variable node RAM block stores the variable node (VN) messages, and the Check node RAM block stores the check node (CN) messages. The Functional Unit block calculates the VN messages and CN messages based on the layered belief propagation and either the normalized min-sum approximation algorithm or the min-sum approximation algorithm. The Termination/Parity check status block calculates the parity checks and provides the parity check status after each iteration. For more information about the decoding algorithms, see the following sections.

Belief Propagation Decoding

The implementation of the belief propagation algorithm is based on the decoding algorithm presented in [4]. For a transmitted LDPC-encoded codeword c, where $$c=(c_0,c_1,\mathrm{...},c_{n-1})$$, the input to the LDPC decoder is the log-likelihood ratio (LLR) value $$L(c_i)=\log \left(\frac{\mathrm{Pr}(c_i=0|\text{channel output for }{c}_i)}{\mathrm{Pr}(c_i=1|\text{channel output for }{c}_i)}\right)$$.

In each iteration, the key components of the algorithm are updated based on these equations:

$$L(r_{ji})=2\text{atanh}\left({\displaystyle \prod _{i^{\prime }\in V_j\backslash i}\tanh \left(\frac{1}{2}L(q_{i^{\prime }j})\right)}\right)$$,

$$L(q_{ij})=L(c_i)+{\displaystyle \sum _{j^{\prime }\in C_i\backslash j}L(r_{j^{\prime }i})}$$, initialized as $$L(q_{ij})=L(c_i)$$ before the first iteration, and

$$L(Q_i)=L(c_i)+{\displaystyle \sum _{j^{\prime }\in C_i}L(r_{j^{\prime }i})}$$.

At the end of each iteration, $$L(Q_i)$$ is an updated estimate of the LLR value for the transmitted bit $$c_i$$. The value $$L(Q_i)$$ is the soft-decision output for $$c_i$$. If $$L(Q_i)<0$$, the hard-decision output for $$c_i$$ is 1. Otherwise, the output is 0.

Layered Belief Propagation Decoding

The implementation of the layered belief propagation algorithm is based on the decoding algorithm presented in [5], section II.A. The decoding loop iterates over subsets of rows (layers) of the parity-check matrix (PCM). For each row m, in a layer and each bit index j, the implementation updates the key components of the algorithm based on these equations:

(1) $$L(q_{mj})=L(q_j)-R_{mj}$$,

(2) $$A_{mj}={\displaystyle \sum _{\begin{array}{c}n \in N\left(m\right)\\ n\ne j\end{array}}\text{ψ}(L(q_{mn}))}$$,

(3) $$s_{mj}={\displaystyle \prod _{\begin{array}{c}n \in N\left(m\right)\\ n\ne j\end{array}}\text{sign}(L(q_{mn}))}$$,

(4) $$R_{mj}=-s_{mj}\text{ψ}(A_{mj})$$, and

(5) $$L(q_j)=L(q_{mj})+R_{mj}$$.

For each layer, the decoding equation (5) works on the combined input obtained from the current LLR inputs $$L(q_{mj})$$ and the previous layer updates $$R_{mj}$$.

Because only a subset of the nodes is updated in a layer, the layered belief propagation algorithm is faster than the belief propagation algorithm. To achieve the same error rate as attained with belief propagation decoding, use half the number of decoding iterations when using the layered belief propagation algorithm.

Min-Sum Approximation

The implementation of the min-sum approximation algorithm follows the layered belief propagation algorithm with equation (2) replaced by

$$A_{mj}=\underset{\begin{array}{c}n \in N\left(m\right)\\ n\ne j\end{array}}{\min }(\left|L(q_{mn}) \right|\cdot \alpha )$$,

where α is 1.

Latency

The latency of the block varies based on the selected Configuration type parameter value, the values of the blkLenIdx and codeRateIdx input ports, and the number of iterations. Because the latency varies, use the nextFrame control signal output port to determine when the block is ready for a new input frame.

The latency of the block is equal to rt + d + L. In this calculation, r is the number of iterations, t is the number of clocks required to decode one iteration, d is the pipeline delay, and L is the length of the input data.

Configuration Type	Code Rate	Block Length	Number Of Clocks Per Iteration	Pipleline Delay (d)
(8160,7136) LDPC	7/8	8160	2080	27 for scalar and 26 for vector
AR4JA LDPC	1/2	2048	252	10
		8192	1240
		32768	4960
	2/3	1536	316
		6144	844
		24576	3376
	4/5	1280	444
		5120	482
		204800	2584

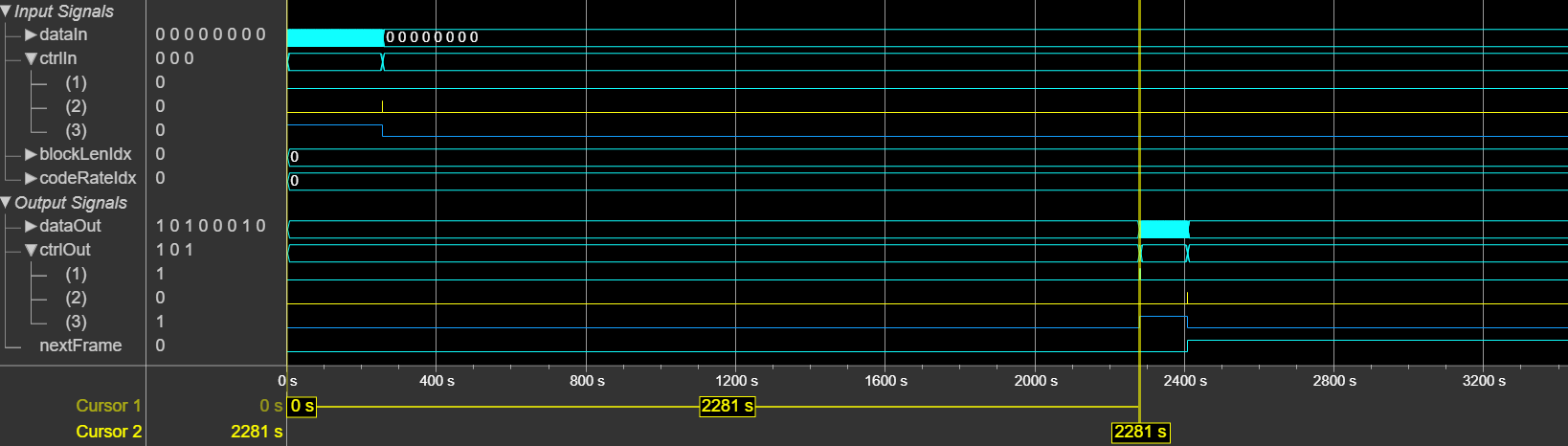
This figure shows a sample output and latency of the CCSDS LDPC Decoder block for a vector input when you set the Configuration type parameter to AR4JA LDPC, the Decoding termination criteria parameter to Max, the Number of iterations parameter to 8, and the codeRateIdx input port value to 0. The latency of the block is 2281 clock cycles.

EbNo and BER Plots

This section shows the EbNo and BER plots of the block for specified inputs and parameter settings.

This plot shows the performance of the block for a 4 bit BPSK modulated LLR input when you set the Configuration type parameter to (8160,7136) LDPC.

This plot shows the performance of the block for a 4 bit BPSK modulated LLR input for a block length of 1024 with code rates of 1/2, 2/3, and 4/5, respectively, when you set the Configuration type parameter to AR4JA LDPC.

This plot shows the performance of the block for a 4 bit BPSK modulated LLR input for a block length of 4096 with code rates of 1/2, 2/3, and 4/5, respectively, when you set the Configuration type parameter to AR4JA LDPC.

This plot shows the performance of the block for a 4 bit BPSK modulated LLR input for a block length of 16384 with code rates of 1/2, 2/3, and 4/5, respectively, when you set the Configuration type parameter to AR4JA LDPC.

Performance

The performance of the synthesized HDL code varies with the target and synthesis options. The performance also varies based on the type of algorithm, decoding termination criteria, and the word length of the input LLR values.

This table shows the resource and performance data synthesis results of the block for the supported CCSDS standards when you set the Configuration type parameter to (8160,7136) LDPC or AR4JA LDPC, the Number of iterations parameter to 8, and the input LLR values as a value with the fixdt(1,4,0). The generated HDL targets to the Xilinx^® Zynq^®Ultrascale+™ MPSoC - ZCU102 Evaluation Board.

Configuration Type	Input Type	Slice LUTs	Slice Registers	Block RAMs	Maximum Frequency in MHz
(8160,7136) LDPC	Scalar	20201	14749	96	377.1
	Vector	20580	15146	96	372.4
AR4JA LDPC	Scalar	29753	19786	192	291.9
	Vector	28812	19854	192	287.9

This block has similar implementation for scalar and vector inputs. So, you do not find substantial difference in the resource utilization and latency.

References

[1] TM Synchronization and Channel Coding. Recommendation for Space Data System Standards. CCSDS 131.0-B-3. Blue Book. Issue 3. Washington, D.C.: CCSDS, September 2017.

[2] TM Synchronization and Channel Coding. Summary of Concept and Rationale CCSDS 130.1-G-3. Green Book. Issue 3, June 2020.

[3] Stephen B. Wicker. Error Control Systems for Digital Communication and Storage. Prentice Hall, 1995.

[4] Gallager, R. “Low-Density Parity-Check Codes.” IEEE Transactions on Information Theory 8, no. 1 (January 1962): 21–28. https://doi.org/10.1109/TIT.1962.1057683.

[5] Hocevar, D.E. “A Reduced Complexity Decoder Architecture via Layered Decoding of LDPC Codes.” In IEEE Workshop OnSignal Processing Systems, 2004. SIPS 2004., 107–12. Austin, Texas, USA: IEEE, 2004. https://doi.org/10.1109/SIPS.2004.1363033.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using Simulink® Coder™.

This block supports C/C++ code generation for Simulink^® accelerator and rapid accelerator modes and for DPI component generation.

HDL Code Generation

Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.

HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.

HDL Architecture

This block has one default HDL architecture.

HDL Block Properties

ConstrainedOutputPipeline	Number of registers to place at the outputs by moving existing delays within your design. Distributed pipelining does not redistribute these registers. The default is 0. For more details, see ConstrainedOutputPipeline (HDL Coder).
InputPipeline	Number of input pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see InputPipeline (HDL Coder).
OutputPipeline	Number of output pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see OutputPipeline (HDL Coder).

Restrictions

You cannot generate HDL for this block inside a Resettable Synchronous Subsystem (HDL Coder).

Version History

Introduced in R2022b