zpk
Zero-pole-gain model
Description
Use zpk to create zero-pole-gain models, or to convert dynamic system models to zero-pole-gain
form.
Zero-pole-gain models are a representation of transfer functions in factorized form. For example, consider the following continuous-time SISO transfer function:
G(s) can be factorized into the zero-pole-gain form as:
A more general representation of the SISO zero-pole-gain model is as follows:
Here, z and p are the vectors of real-valued or complex-valued zeros and poles, and k is the real-valued or complex-valued scalar gain. For MIMO models, each I/O channel is represented by one such transfer function hij(s).
You can create a zero-pole-gain model object either by specifying the poles, zeros and
gains directly, or by converting a model of another type (such as a state-space model
ss) to zero-pole-gain form.
You can also use zpk to create generalized state-space (genss) models or uncertain state-space (uss (Robust Control Toolbox)) models.
Creation
Syntax
Description
Create ZPK Model
sys = zpk(zeros,poles,gain)zeros and
poles specified as vectors and the scalar value of
gain. The output sys is a
zpk model object storing the model data. Set
zeros or poles to [] for
systems without zeros or poles. These two inputs need not have equal length and the
model need not be proper (that is, have an excess of poles).
sys = zpk(___,PropertyName=Value)
Convert To ZPK Model
sys = zpk(ltiSys,Name=Value)zpk representation of the sparse model
ltiSys by computing zeros and poles based on one or more
specified name-value arguments. Because this method calculates zeros for each
input-output pair, it is most suitable for models with small input-output sizes. (since R2025a)
Create Variable for Rational Expression
s = zpk('s') creates a special variable s
that you can use in a rational expression to create a continuous-time zero-pole-gain
model. Using a rational expression is sometimes easier and more intuitive than
specifying polynomial coefficients.
Input Arguments
Zeros of the zero-pole-gain model, specified as:
A row vector for SISO models. For instance, use
[1,2+i,2-i]to create a model with zeros ats = 1,s = 2+i, ands = 2-i. For an example, see Continuous-Time SISO Zero-Pole-Gain Model.An
Ny-by-Nucell array of row vectors to specify a MIMO zero-pole-gain model, whereNyis the number of outputs, andNuis the number of inputs. For an example, see Discrete-Time MIMO Zero-Pole-Gain Model.
For instance, if a is realp tunable
parameter with nominal value 3, then you can use zeros =
[1 2 a] to create a genss model with zeros at
s = 1 and s = 2 and a tunable zero at
s = 3.
When you use this input argument to create a zpk model, the
argument sets the initial value of the property Z.
Poles of the zero-pole-gain model, specified as:
A row vector for SISO models. For an example, see Continuous-Time SISO Zero-Pole-Gain Model.
An
Ny-by-Nucell array of row vectors to specify a MIMO zero-pole-gain model, whereNyis the number of outputs andNuis the number of inputs. For an example, see Discrete-Time MIMO Zero-Pole-Gain Model.
Also a property of the zpk object. This input argument sets
the initial value of property P.
Gain of the zero-pole-gain model, specified as:
A scalar for SISO models. For an example, see Continuous-Time SISO Zero-Pole-Gain Model.
An
Ny-by-Numatrix to specify a MIMO zero-pole-gain model, whereNyis the number of outputs andNuis the number of inputs. For an example, see Discrete-Time MIMO Zero-Pole-Gain Model.
Also a property of the zpk object. This input argument sets
the initial value of property K.
Sample time, specified as a scalar. Also a property of the zpk
object. This input argument sets the initial value of property Ts.
Dynamic system, specified as a SISO or MIMO dynamic system model or array of dynamic system models. Dynamic systems that you can use include:
Continuous-time or discrete-time numeric LTI models, such as
tf,zpk,ss, orpidmodels.If
ltiSysis a sparse state-space model (sparssormechss), the software computes a truncated zero-pole-gain approximation in a specified frequency band of focus. For sparse models, use the name-value arguments to specify computation options. If you do not specify any options, the software computes up to the first 1000 poles and zeros with smallest magnitude. Additionally, obtaining a truncated zero-pole-gain approximation is applicable only for models with a validsparssrepresentation. (since R2025a)Generalized or uncertain LTI models such as
genssoruss(Robust Control Toolbox) models. (Using uncertain models requires a Robust Control Toolbox™ license.)The resulting zero-pole-gain model assumes
current values of the tunable components for tunable control design blocks.
nominal model values for uncertain control design blocks.
Identified LTI models, such as
idtf(System Identification Toolbox),idss(System Identification Toolbox),idproc(System Identification Toolbox),idpoly(System Identification Toolbox), andidgrey(System Identification Toolbox) models. To select the component of the identified model to convert, specifycomponent. If you do not specifycomponent,tfconverts the measured component of the identified model by default. (Using identified models requires System Identification Toolbox™ software.)An identified nonlinear model cannot be converted into a
zpkmodel object. You may first use linear approximation functions such aslinearizeandlinapp(This functionality requires System Identification Toolbox software.)
Static gain, specified as a scalar or matrix. Static gain or steady state gain of a system represents the ratio of the output to the input under steady state condition.
Component of identified model to convert, specified as one of the following:
'measured'— Convert the measured component ofsys.'noise'— Convert the noise component ofsys'augmented'— Convert both the measured and noise components ofsys.
component only applies when sys is an
identified LTI model.
For more information on identified LTI models and their measured and noise components, see Identified LTI Models.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: sys = zpk(sparseSys,Focus=[0
100],Display="off")
Since R2025a
Use parallel computing during zero-pole computation, specified as a numeric or
logical 0 (false) or 1
(true).
When UseParallel is set to true, you can
explicitly choose to scale to your preferred parallel environment. Enabling parallel
computing may result in improved performance during zero-pole computation. However,
even with UseParallel set to false, the
algorithm can use built-in multithreading to make best use of the local resources.
For more information, see MATLAB
Multicore.
This option requires a Parallel Computing Toolbox™ license.
Since R2025a
Roll-off slope, specified as a nonpositive scalar or matrix.
Use a scalar value for SISO models or when the slope is uniform for all input-output pairs for MIMO models.
Use a matrix when the slope is different for each input-output pair for MIMO models.
This option allows you to specify how the approximation should roll-off past the
specified frequency range. For example, Slope of
-2 ensures the gain rolls off at a rate of at least –40
dB/decade (the roll-off rate of 1/s2)
beyond fmax.
Since R2025a
Frequency range of interest, specified as a vector of form
[0,fmax]. When you specify a frequency range of focus, the
software computes only the poles with natural frequency in this range. For
discrete-time models, the software approximates the equivalent natural frequency
through Tustin transform.
Since zpk computes all poles and zeros in the specified
frequency range, you typically specify a low-frequency range to limit computing a
large number of poles and zeros. By default, the focus is unspecified ([0
Inf]) and the algorithm computes up to MaxNumber
poles and zeros.
Since R2025a
Maximum number of poles and zeros to compute, specified as a positive integer. This value limits the number of poles and zeros computed by the algorithm and the order of the approximation of the original sparse model.
Since R2025a
Spectral shift, specified as a finite scalar.
The software computes poles with the natural frequency in the specified range
[0,fmax] using inverse power iterations for
A-sigma*E, which obtains eigenvalues closest to the shift
sigma. When A is singular and
sigma is zero, the algorithm fails as no inverse exists.
Therefore, for sparse models with integral action (s = 0 or at
z = 1 for discrete-time models), you can use this option to
implicitly shift poles or zeros to the value closest to this shift value. Specify a
shift value that is not equal to an existing pole or zero value of the original
model.
Since R2025a
Tolerance for accuracy of computed poles and zeros, specified as a positive finite scalar. This value controls the convergence of computed eigenvalues in inverse power iterations.
Since R2025a
Show or hide progress report, specified as either "off" or
"on".
Output Arguments
Output system model, returned as:
A zero-pole-gain (
zpk) model object, when thezeros,polesandgaininput arguments contain numeric values.sysis always azpkmodel object when convertingltiSystozpkmodel type.A generalized state-space model (
genss) object, when thezeros,polesandgaininput arguments includes tunable parameters, such asrealpparameters or generalized matrices (genmat).An uncertain state-space model (
uss) object, when thezeros,polesandgaininput arguments includes uncertain parameters. Using uncertain models requires a Robust Control Toolbox license.
Properties
System zeros, specified as:
A cell array of transfer function zeros or the numerator roots for SISO models.
An
Ny-by-Nucell array of row vectors of the zeros for each I/O pair in a MIMO model, whereNyis the number of outputs andNuis the number of inputs.
The values of Z can be either real-valued or
complex-valued.
System poles, specified as:
A cell array of transfer function poles or the denominator roots for SISO models.
An
Ny-by-Nucell array of row vectors of the poles for each I/O pair in a MIMO model, whereNyis the number of outputs andNuis the number of inputs.
The values of P can be either real-valued or
complex-valued.
System gains, specified as:
A scalar value for SISO models.
An
Ny-by-Numatrix storing the gain values for each I/O pair of the MIMO model, whereNyis the number of outputs andNuis the number of inputs.
The values of K can be either real-valued or complex-valued.
Specifies how the numerator and denominator polynomials are factorized for display, specified as one of the following:
'roots'— Display factors in terms of the location of the polynomial roots.'roots'is the default value ofDisplayFormat.'frequency'— Display factors in terms of root natural frequencies ω0 and damping ratios ζ.The
'frequency'display format is not available for discrete-time models withVariablevalue'z^-1'or'q^-1'.'time constant'— Display factors in terms of root time constants τ and damping ratios ζ.The
'time constant'display format is not available for discrete-time models withVariablevalue'z^-1'or'q^-1'.
For continuous-time models, the following table shows how the polynomial factors are arranged in each display format.
DisplayName Value | First-Order Factor (Real Root ) | Second-Order Factor (Complex Root pair ) |
|---|---|---|
'roots' | where | |
'frequency' | where | where |
'time constant' | where | where |
For discrete-time models, the polynomial factors are arranged similar to the continuous-time models, with the following variable substitutions:
where Ts is the sample time. In discrete-time, τ and ω0 closely match the time constant and natural frequency of the equivalent continuous-time root, provided that the following condition is fulfilled: .
Zero-pole-gain model display variable, specified as one of the following:
's'— Default for continuous-time models'z'— Default for discrete-time models'p'— Equivalent to's''q'— Equivalent to'z''z^-1'— Inverse of'z''q^-1'— Equivalent to'z^-1'
Transport delay, specified as one of the following:
Scalar — Specify the transport delay for a SISO system or the same transport delay for all input/output pairs of a MIMO system.
Ny-by-Nuarray — Specify separate transport delays for each input/output pair of a MIMO system. Here,Nyis the number of outputs andNuis the number of inputs.
For continuous-time systems, specify transport delays in the time unit specified by
the TimeUnit property. For discrete-time systems, specify transport
delays in integer multiples of the sample time, Ts. For more
information on time delay, see Time Delays in Linear Systems.
Input delay for each input channel, specified as one of the following:
Scalar — Specify the input delay for a SISO system or the same delay for all inputs of a multi-input system.
Nu-by-1 vector — Specify separate input delays for input of a multi-input system, whereNuis the number of inputs.
For continuous-time systems, specify input delays in the time unit specified by the TimeUnit property. For discrete-time systems, specify input delays in integer multiples of the sample time, Ts.
For more information, see Time Delays in Linear Systems.
Output delay for each output channel, specified as one of the following:
Scalar — Specify the output delay for a SISO system or the same delay for all outputs of a multi-output system.
Ny-by-1 vector — Specify separate output delays for output of a multi-output system, whereNyis the number of outputs.
For continuous-time systems, specify output delays in the time unit specified by the TimeUnit property. For discrete-time systems, specify output delays in integer multiples of the sample time, Ts.
For more information, see Time Delays in Linear Systems.
Sample time, specified as:
0for continuous-time systems.A positive scalar representing the sampling period of a discrete-time system. Specify
Tsin the time unit specified by theTimeUnitproperty.-1for a discrete-time system with an unspecified sample time.
Time variable units, specified as one of the following:
'nanoseconds''microseconds''milliseconds''seconds''minutes''hours''days''weeks''months''years'
Changing TimeUnit has no effect on other properties, but changes the overall system behavior. Use chgTimeUnit to convert between time units without modifying system behavior.
Input channel names, specified as one of the following:
A character vector, for single-input models.
A cell array of character vectors, for multi-input models.
'', no names specified, for any input channels.
Alternatively, you can assign input names for multi-input models using automatic vector
expansion. For example, if sys is a two-input model, enter the
following.
sys.InputName = 'controls';The input names automatically expand to {'controls(1)';'controls(2)'}.
You can use the shorthand notation u to refer to the InputName property. For example, sys.u is equivalent to sys.InputName.
Use InputName to:
Identify channels on model display and plots.
Extract subsystems of MIMO systems.
Specify connection points when interconnecting models.
Input channel units, specified as one of the following:
A character vector, for single-input models.
A cell array of character vectors, for multi-input models.
'', no units specified, for any input channels.
Use InputUnit to specify input signal units. InputUnit has no effect on system behavior.
Input channel groups, specified as a structure. Use InputGroup to assign
the input channels of MIMO systems into groups and refer to each group by name. The
field names of InputGroup are the group names and the field values
are the input channels of each group. For example, enter the following to create input
groups named controls and noise that include input
channels 1 and 2, and 3 and
5, respectively.
sys.InputGroup.controls = [1 2]; sys.InputGroup.noise = [3 5];
You can then extract the subsystem from the controls inputs to all outputs
using the following.
sys(:,'controls')By default, InputGroup is a structure with no fields.
Output channel names, specified as one of the following:
A character vector, for single-output models.
A cell array of character vectors, for multi-output models.
'', no names specified, for any output channels.
Alternatively, you can assign output names for multi-output models using automatic vector
expansion. For example, if sys is a two-output model, enter the
following.
sys.OutputName = 'measurements';The output names automatically expand to {'measurements(1)';'measurements(2)'}.
You can also use the shorthand notation y to refer to the OutputName property. For example, sys.y is equivalent to sys.OutputName.
Use OutputName to:
Identify channels on model display and plots.
Extract subsystems of MIMO systems.
Specify connection points when interconnecting models.
Output channel units, specified as one of the following:
A character vector, for single-output models.
A cell array of character vectors, for multi-output models.
'', no units specified, for any output channels.
Use OutputUnit to specify output signal units. OutputUnit has no effect on system behavior.
Output channel groups, specified as a structure. Use OutputGroup to
assign the output channels of MIMO systems into groups and refer to each group by name.
The field names of OutputGroup are the group names and the field
values are the output channels of each group. For example, create output groups named
temperature and measurement that include
output channels 1, and 3 and 5,
respectively.
sys.OutputGroup.temperature = [1]; sys.OutputGroup.measurement = [3 5];
You can then extract the subsystem from all inputs to the measurement
outputs using the following.
sys('measurement',:)By default, OutputGroup is a structure with no fields.
System name, specified as a character vector. For example, 'system_1'.
User-specified text that you want to associate with the system, specified as a character vector or cell array of character vectors. For example, 'System is MIMO'.
User-specified data that you want to associate with the system, specified as any MATLAB data type.
Sampling grid for model arrays, specified as a structure array.
Use SamplingGrid to track the variable values associated with each model in a model array, including identified linear time-invariant (IDLTI) model arrays.
Set the field names of the structure to the names of the sampling variables. Set the field values to the sampled variable values associated with each model in the array. All sampling variables must be numeric scalars, and all arrays of sampled values must match the dimensions of the model array.
For example, you can create an 11-by-1 array of linear models, sysarr, by taking snapshots of a linear time-varying system at times t = 0:10. The following code stores the time samples with the linear models.
sysarr.SamplingGrid = struct('time',0:10)Similarly, you can create a 6-by-9 model array, M, by independently sampling two variables, zeta and w. The following code maps the (zeta,w) values to M.
[zeta,w] = ndgrid(<6 values of zeta>,<9 values of w>) M.SamplingGrid = struct('zeta',zeta,'w',w)
When you display M, each entry in the array includes the corresponding zeta and w values.
M
M(:,:,1,1) [zeta=0.3, w=5] =
25
--------------
s^2 + 3 s + 25
M(:,:,2,1) [zeta=0.35, w=5] =
25
----------------
s^2 + 3.5 s + 25
...For model arrays generated by linearizing a Simulink® model at multiple parameter values or operating points, the software populates SamplingGrid automatically with the variable values that correspond to each entry in the array. For instance, the Simulink
Control Design™ commands linearize (Simulink Control Design) and slLinearizer (Simulink Control Design) populate SamplingGrid automatically.
By default, SamplingGrid is a structure with no fields.
Object Functions
The following lists contain a representative subset of the functions you can use with
zpk models. In general, any function applicable to Dynamic System Models is
applicable to a zpk object.
step | Step response of dynamic system |
impulse | Impulse response plot of dynamic system; impulse response data |
lsim | Compute time response simulation data of dynamic system to arbitrary inputs |
bode | Bode frequency response of dynamic system |
nyquist | Nyquist response of dynamic system |
nichols | Nichols response of dynamic system |
bandwidth | Frequency response bandwidth |
Examples
For this example, consider the following continuous-time SISO zero-pole-gain model:
Specify the zeros, poles and gain, and create the SISO zero-pole-gain model.
zeros = 0; poles = [1-1i 1+1i 2]; gain = -2; sys = zpk(zeros,poles,gain)
sys =
-2 s
--------------------
(s-2) (s^2 - 2s + 2)
Continuous-time zero/pole/gain model.
Model Properties
For this example, consider the following SISO discrete-time zero-pole-gain model with 0.1s sample time:
Specify the zeros, poles, gains and the sample time, and create the discrete-time SISO zero-pole-gain model.
zeros = [1 2 3]; poles = [6 5 4]; gain = 7; ts = 0.1; sys = zpk(zeros,poles,gain,ts)
sys = 7 (z-1) (z-2) (z-3) ------------------- (z-6) (z-5) (z-4) Sample time: 0.1 seconds Discrete-time zero/pole/gain model. Model Properties
In this example, you create a MIMO zero-pole-gain model by concatenating SISO zero-pole-gain models. Consider the following single-input, two-output continuous-time zero-pole-gain model:
Specify the MIMO zero-pole-gain model by concatenating the SISO entries.
zeros1 = 1; poles1 = -1; gain = 1; sys1 = zpk(zeros1,poles1,gain)
sys1 = (s-1) ----- (s+1) Continuous-time zero/pole/gain model. Model Properties
zeros2 = -2; poles2 = [-2+1i -2-1i]; sys2 = zpk(zeros2,poles2,gain)
sys2 =
(s+2)
--------------
(s^2 + 4s + 5)
Continuous-time zero/pole/gain model.
Model Properties
sys = [sys1;sys2]
sys =
From input to output...
(s-1)
1: -----
(s+1)
(s+2)
2: --------------
(s^2 + 4s + 5)
Continuous-time zero/pole/gain model.
Model Properties
Create a zero-pole-gain model for the discrete-time, multi-input, multi-output model:
with sample time ts = 0.2 seconds.
Specify the zeros and poles as cell arrays and the gains as an array.
zeros = {[] 0;2 []};
poles = {-0.3 -0.3;-0.3 -0.3};
gain = [1 1;-1 3];
ts = 0.2;Create the discrete-time MIMO zero-pole-gain model.
sys = zpk(zeros,poles,gain,ts)
sys =
From input 1 to output...
1
1: -------
(z+0.3)
- (z-2)
2: -------
(z+0.3)
From input 2 to output...
z
1: -------
(z+0.3)
3
2: -------
(z+0.3)
Sample time: 0.2 seconds
Discrete-time zero/pole/gain model.
Model Properties
Specify the zeros, poles and gain along with the sample time and create the zero-pole-gain model, specifying the state and input names using name-value pairs.
zeros = 4; poles = [-1+2i -1-2i]; gain = 3; ts = 0.05; sys = zpk(zeros,poles,gain,ts,'InputName','Force')
sys =
From input "Force" to output:
3 (z-4)
--------------
(z^2 + 2z + 5)
Sample time: 0.05 seconds
Discrete-time zero/pole/gain model.
Model Properties
The number of input names must be consistent with the number of zeros.
Naming the inputs and outputs can be useful when dealing with response plots for MIMO systems.
step(sys)

Notice the input name Force in the title of the step response plot.
For this example, create a continuous-time zero-pole-gain model using rational expressions. Using a rational expression can sometimes be easier and more intuitive than specifying poles and zeros.
Consider the following system:
To create the transfer function model, first specify s as a zpk object.
s = zpk('s')s = s Continuous-time zero/pole/gain model. Model Properties
Create the zero-pole-gain model using s in the rational expression.
sys = s/(s^2 + 2*s + 10)
sys =
s
---------------
(s^2 + 2s + 10)
Continuous-time zero/pole/gain model.
Model Properties
For this example, create a discrete-time zero-pole-gain model using a rational expression. Using a rational expression can sometimes be easier and more intuitive than specifying poles and zeros.
Consider the following system:
To create the zero-pole-gain model, first specify z as a zpk object and the sample time ts.
ts = 0.1;
z = zpk('z',ts)z = z Sample time: 0.1 seconds Discrete-time zero/pole/gain model. Model Properties
Create the zero-pole-gain model using z in the rational expression.
sys = (z - 1) / (z^2 - 1.85*z + 0.9)
sys =
(z-1)
-------------------
(z^2 - 1.85z + 0.9)
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
Model Properties
For this example, create a zero-pole-gain model with properties inherited from another zero-pole-gain model. Consider the following two zero-pole-gain models:
For this example, create sys1 with the TimeUnit and InputDelay property set to 'minutes'.
zero1 = 0; pole1 = [0;-8]; gain1 = 2; sys1 = zpk(zero1,pole1,gain1,'TimeUnit','minutes','InputUnit','minutes')
sys1 =
2 s
-------
s (s+8)
Continuous-time zero/pole/gain model.
Model Properties
propValues1 = [sys1.TimeUnit,sys1.InputUnit]
propValues1 = 1×2 cell
{'minutes'} {'minutes'}
Create the second zero-pole-gain model with properties inherited from sys1.
zero = 1; pole = [-3,5]; gain2 = 0.8; sys2 = zpk(zero,pole,gain2,sys1)
sys2 = 0.8 (s-1) ----------- (s+3) (s-5) Continuous-time zero/pole/gain model. Model Properties
propValues2 = [sys2.TimeUnit,sys2.InputUnit]
propValues2 = 1×2 cell
{'minutes'} {'minutes'}
Observe that the zero-pole-gain model sys2 has that same properties as sys1.
Consider the following two-input, two-output static gain matrix m:
Specify the gain matrix and create the static gain zero-pole-gain model.
m = [2,4;...
3,5];
sys1 = zpk(m)sys1 = From input 1 to output... 1: 2 2: 3 From input 2 to output... 1: 4 2: 5 Static gain. Model Properties
You can use static gain zero-pole-gain model sys1 obtained above to cascade it with another zero-pole-gain model.
sys2 = zpk(0,[-1 7],1)
sys2 =
s
-----------
(s+1) (s-7)
Continuous-time zero/pole/gain model.
Model Properties
sys = series(sys1,sys2)
sys =
From input 1 to output...
2 s
1: -----------
(s+1) (s-7)
3 s
2: -----------
(s+1) (s-7)
From input 2 to output...
4 s
1: -----------
(s+1) (s-7)
5 s
2: -----------
(s+1) (s-7)
Continuous-time zero/pole/gain model.
Model Properties
For this example, compute the zero-pole-gain model of the following state-space model:
Create the state-space model using the state-space matrices.
A = [-2 -1;1 -2]; B = [1 1;2 -1]; C = [1 0]; D = [0 1]; ltiSys = ss(A,B,C,D);
Convert the state-space model ltiSys to a zero-pole-gain model.
sys = zpk(ltiSys)
sys =
From input 1 to output:
s
--------------
(s^2 + 4s + 5)
From input 2 to output:
(s^2 + 5s + 8)
--------------
(s^2 + 4s + 5)
Continuous-time zero/pole/gain model.
Model Properties
You can use a for loop to specify an array of zero-pole-gain models.
First, pre-allocate the zero-pole-gain model array with zeros.
sys = zpk(zeros(1,1,3));
The first two indices represent the number of outputs and inputs for the models, while the third index is the number of models in the array.
Create the zero-pole-gain model array using a rational expression in the for loop.
s = zpk('s'); for k = 1:3 sys(:,:,k) = k/(s^2+s+k); end sys
sys(:,:,1,1) =
1
-------------
(s^2 + s + 1)
sys(:,:,2,1) =
2
-------------
(s^2 + s + 2)
sys(:,:,3,1) =
3
-------------
(s^2 + s + 3)
3x1 array of continuous-time zero/pole/gain models.
Model Properties
For this example, extract the measured and noise components of an identified polynomial model into two separate zero-pole-gain models.
Load the Box-Jenkins polynomial model ltiSys in identifiedModel.mat.
load('identifiedModel.mat','ltiSys');
ltiSys is an identified discrete-time model of the form: , where represents the measured component and the noise component.
Extract the measured and noise components as zero-pole-gain models.
sysMeas = zpk(ltiSys,'measured') sysMeas =
From input "u1" to output "y1":
-0.14256 z^-1 (1-1.374z^-1)
z^(-2) * -----------------------------
(1-0.8789z^-1) (1-0.6958z^-1)
Sample time: 0.04 seconds
Discrete-time zero/pole/gain model.
Model Properties
sysNoise = zpk(ltiSys,'noise')sysNoise =
From input "v@y1" to output "y1":
0.045563 (1+0.7245z^-1)
--------------------------------------------
(1-0.9658z^-1) (1 - 0.0602z^-1 + 0.2018z^-2)
Input groups:
Name Channels
Noise 1
Sample time: 0.04 seconds
Discrete-time zero/pole/gain model.
Model Properties
The measured component can serve as a plant model, while the noise component can be used as a disturbance model for control system design.
For this example, create a SISO zero-pole-gain model with an input delay of 0.5 seconds and an output delay of 2.5 seconds.
zeros = 5; poles = [7+1i 7-1i -3]; gains = 1; sys = zpk(zeros,poles,gains,'InputDelay',0.5,'OutputDelay',2.5)
sys =
(s-5)
exp(-3*s) * ----------------------
(s+3) (s^2 - 14s + 50)
Continuous-time zero/pole/gain model.
Model Properties
You can also use the get command to display all the properties of a MATLAB object.
get(sys)
Z: {[5]}
P: {[3×1 double]}
K: 1
DisplayFormat: 'roots'
Variable: 's'
IODelay: 0
InputDelay: 0.5000
OutputDelay: 2.5000
InputName: {''}
InputUnit: {''}
InputGroup: [1×1 struct]
OutputName: {''}
OutputUnit: {''}
OutputGroup: [1×1 struct]
Notes: [0×1 string]
UserData: []
Name: ''
Ts: 0
TimeUnit: 'seconds'
SamplingGrid: [1×1 struct]
For more information on specifying time delay for an LTI model, see Specifying Time Delays.
For this example, design a 2-DOF PID controller with a target bandwidth of 0.75 rad/s for a system represented by the following zero-pole-gain model:
Create a zero-pole-gain model object sys using the zpk command.
zeros = []; poles = [-0.25+0.2i;-0.25-0.2i]; gain = 1; sys = zpk(zeros,poles,gain)
sys =
1
---------------------
(s^2 + 0.5s + 0.1025)
Continuous-time zero/pole/gain model.
Model Properties
Using the target bandwidth, use pidtune to generate a 2-DOF controller.
wc = 0.75;
C2 = pidtune(sys,'PID2',wc)C2 =
1
u = Kp (b*r-y) + Ki --- (r-y) + Kd*s (c*r-y)
s
with Kp = 0.512, Ki = 0.0975, Kd = 0.574, b = 0.38, c = 0
Continuous-time 2-DOF PID controller in parallel form.
Model Properties
Using the type 'PID2' causes pidtune to generate a 2-DOF controller, represented as a pid2 object. The display confirms this result. The display also shows that pidtune tunes all controller coefficients, including the setpoint weights b and c, to balance performance and robustness.
For interactive PID tuning in the Live Editor, see the Tune PID Controller Live Editor task. This task lets you interactively design a PID controller and automatically generates MATLAB code for your live script.
For interactive PID tuning in a standalone app, use PID Tuner. See PID Controller Design for Fast Reference Tracking for an example of designing a controller using the app.
Since R2025a
This example shows how to obtain a truncated zero-pole-gain model of a sparse state-space model. This example uses a sparse model obtained from linearizing a thermal model of heat distribution in a circular cylindrical rod.
Load the model data.
load cylindricalRod.mat
sys = sparss(A,B,C,D,E);
w = logspace(-7,-1,20);
size(sys)Sparse state-space model with 3 outputs, 1 inputs, and 7522 states.
Analyze the frequency response of the model.
sigmaplot(sys,w)

To obtain a truncated approximation, use zpk and specify the frequency band of focus. For this model, you can use a frequency range from 0 rad/s to 0.01 rad/s to obtain the low-order approximation.
zsys = zpk(sys,Focus=[0 1e-2],Display="off");Compare the frequency response.
sigmaplot(sys,zsys,w)
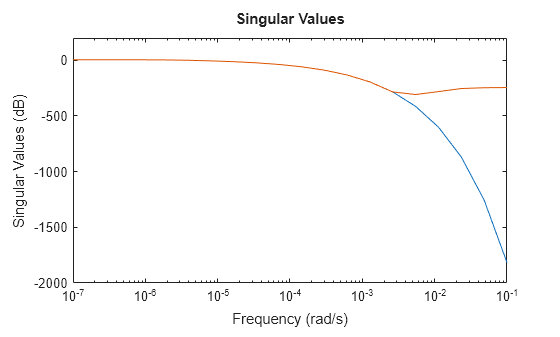
This thermal model has a very steep roll-off beyond 0.001 rad/s. By default, the reduced model obtained using zpk does not provide a good match for this roll-off. To mitigate this, you can use the RollOff argument of zpk and specify a minimum roll-off value beyond the frequency band of focus. Specify a roll-off slope value of -45, which corresponds to a rate of at least –900 db/decade.
zsys2 = zpk(sys,Focus=[0 1e-2],RollOff=-45,Display="off");
sigmaplot(sys,zsys2,w)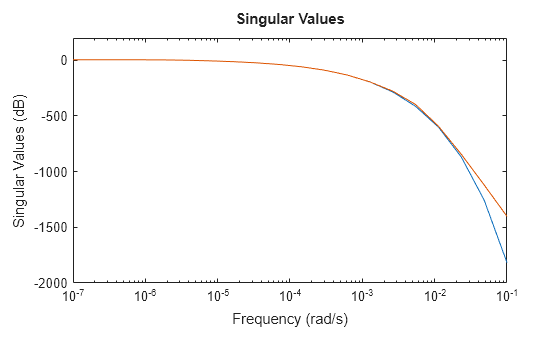
The reduced model now provides a much better approximation of the roll-off value. However, in this example, readjusting roll-off slope using zpk requires recomputing zeros and poles. This may be computationally expensive in case of large-scale models. As an alternative, you can use the zero-pole truncation method of reducespec and adjust roll-off at no extra computation cost, after the software has computed poles and zeros. For an example, see Zero-Pole Truncation of Thermal Model.
Algorithms
zpk uses the MATLAB function roots to convert transfer functions and the
functions zero and pole to convert state-space models.
To convert sparse models, zpk uses the Krylov--Schur algorithm [1] for
inverse power iterations to compute poles and zeros in the specified frequency band.
References
[1] Stewart, G. W. “A Krylov--Schur Algorithm for Large Eigenproblems.” SIAM Journal on Matrix Analysis and Applications 23, no. 3 (January 2002): 601–14. https://doi.org/10.1137/S0895479800371529.
Version History
Introduced before R2006aYou can now use zpk to convert sparse state-space models and obtain a
truncated zero-pole-gain approximation. zpk computes a subset of the zeros
and poles of sparse models, typically in a specific low-frequency band [0
fmax]. This can yield better low-frequency
approximations than modal truncation model-order reduction at the expense of more
computation. zpk also provides direct control over the roll-off slope past
the frequency fmax. Use the new syntax
zsys = zpk(sparseSys,Name=Value) to obtain an approximation based on
specified options, such as frequency range of focus. For an example, see Compute Truncated ZPK Approximation of Sparse Model.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)