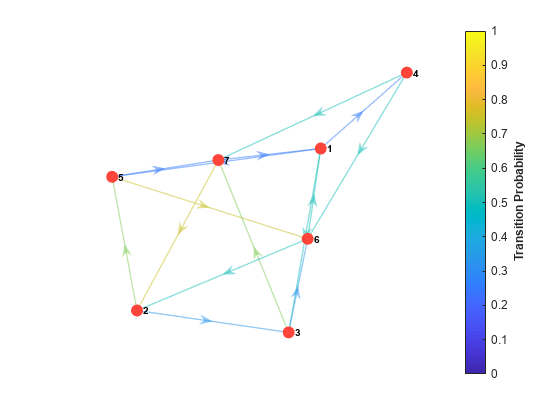
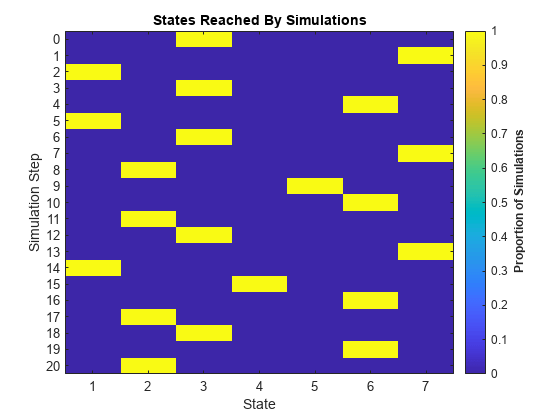
simulate
Simulate Markov chain state walks
Description
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Tips
To start
nsimulations from statek, use:X0 = zeros(1,NumStates); X0(k) = n;
To visualize the data created by
simulate, usesimplot.
Version History
Introduced in R2017b