histogram2
Bivariate histogram plot
Description
Bivariate histograms are a type of bar plot for numeric data that group the
data into 2-D bins. After you create a Histogram2 object, you can
modify aspects of the histogram by changing its property values. This is particularly
useful for quickly modifying the properties of the bins or changing the
display.
Creation
Syntax
Description
histogram2( creates a
bivariate histogram plot of X,Y)X and Y.
The histogram2 function uses an automatic binning
algorithm that returns bins with a uniform area, chosen to cover the range
of elements in X and Y and reveal the
underlying shape of the distribution. histogram2
displays the bins as 3-D rectangular bars such that the height of each bar
indicates the number of elements in the bin.
histogram2(___,
specifies additional parameters using one or more name-value arguments for
any of the previous syntaxes. For example, specify
Name,Value)Normalization to use a different type of
normalization. For a list of properties, see Histogram2 Properties.
histogram2(
plots into the specified axes instead of into the current axes
(ax,___)gca). ax can precede any of the
input argument combinations in the previous syntaxes.
h = histogram2(___)Histogram2 object. Use this to inspect and
adjust properties of the bivariate histogram. For a list of properties, see
Histogram2 Properties.
Input Arguments
Data to distribute among bins, specified as separate arguments of
vectors, matrices, or multidimensional arrays. X and
Y must be the same size.
histogram2 treats matrix or multidimensional
array data as single column vectors, X(:) and
Y(:), and plots a single histogram.
Corresponding elements in X and
Y specify the x and
y coordinates of 2-D data points,
[X(k),Y(k)]. The data types of
X and Y can be different, but
histogram2 concatenates these inputs into a
single N-by-2 matrix of the
dominant data type.
histogram2 ignores all NaN
values. Similarly, histogram2 ignores
Inf and -Inf values, unless
the bin edges explicitly specify Inf or
-Inf as a bin edge. Although
NaN, Inf, and
-Inf values are typically not plotted, they are
still included in normalization calculations that include the total
number of data elements, such as
'probability'.
Note
If X or Y contain integers
of type int64 or uint64 that
are larger than flintmax, then it is recommended
that you explicitly specify the histogram bin
edges.histogram2 automatically bins the
input data using double precision, which lacks integer precision for
numbers greater than flintmax.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Number of bins in each dimension, specified as a positive integer scalar or two-element vector of positive integers.
If
nbinsis a scalar, thenhistogram2uses that many bins in each dimension.If
nbinsis a vector, then the first element gives the number of bins in the x-dimension, and the second element gives the number of bins in the y-dimension.
If you do not specify nbins, then
histogram2 automatically
calculates how many bins to use based on the values in
X and Y.
If you specify nbins with
BinMethod or BinWidth,
histogram2 only honors the
last parameter.
Example: histogram2(X,Y,20) uses 20 bins in each
dimension.
Example: histogram2(X,Y,[10 20]) uses 10 bins in the
x-dimension and 20 bins in the
y-dimension.
Bin edges in x-dimension, specified as a vector. The first element specifies the leading edge of the first bin in the x-dimension. The last element specifies the trailing edge of the last bin in the x-dimension. The trailing edge is only included for the last bin.
If you specify
XedgesandYedgeswithBinMethod,BinWidth, orNumBins,histogram2only honors the bin edges and the bin edges must be specified last.If you specify
XedgeswithXBinLimits,histogram2only honors theXedgesand theXedgesmust be specified last.
Bin edges in y-dimension, specified as a vector. The first element specifies the leading edge of the first bin in the y-dimension. The last element specifies the trailing edge of the last bin in the y-dimension. The trailing edge is only included for the last bin.
If you specify
YedgesandXedgeswithBinMethod,BinWidth, orNumBins,histogram2only honors the bin edges and the bin edges must be specified last.If you specify
YedgeswithYBinLimits,histogram2only honors theYedgesand theYedgesmust be specified last.
Bin counts, specified as a matrix. Use this input to pass bin counts
to histogram2 when the bin counts calculation is
performed separately and you do not want histogram2
to do any data binning.
counts must be a matrix of size
[length(XBinEdges)-1 length(YBinEdges)-1] so that
it specifies a bin count for each bin.
Example: histogram2('XBinEdges',-1:1,'YBinEdges',-2:2,'BinCounts',[1
2 3 4; 5 6 7 8])
Axes object. If you do not specify an axes, then the
histogram2 function uses the current axes
(gca).
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: histogram2(X,Y,BinWidth=[5 10])
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: histogram2(X,Y,'BinWidth',[5 10])
Note
The properties listed here are only a subset. For a complete list, see Histogram2 Properties.
Bins
Width of bins in each dimension, specified as a two-element vector of positive values. The first element gives the width of the bins in the x-dimension, and the second element gives the width of the bins in the y-dimension.
If you specify BinWidth, then histogram2 can use a maximum of 1024 bins (210) along each dimension. If instead the specified bin width requires
more bins, then histogram2 uses a larger bin width
corresponding to the maximum number of bins.
If you specify BinWidth with BinMethod or
NumBins, histogram2 only
honors the last parameter.
Example: histogram2(X,Y,'BinWidth',[5
10])5 in the
x-dimension and size 10 in the
y-dimension.
Bin limits in x-dimension, specified as a two-element vector,
[xbmin,xbmax]. The first element indicates the first bin edge in
the x-dimension. The second element indicates the last bin edge in
the x-dimension.
This option only bins data that falls within the bin limits inclusively,
X>=xbmin & X<=xbmax.
Selection mode for bin limits in x-dimension, specified as
'auto' or 'manual'. The default value is
'auto', so that the bin limits automatically adjust to the data
along the x-axis.
If you explicitly specify either XBinLimits or
XBinEdges, then XBinLimitsMode is set
automatically to 'manual'. In that case, specify
XBinLimitsMode as 'auto' to rescale the bin
limits to the data.
Bin limits in y-dimension, specified as a two-element vector,
[ybmin,ybmax]. The first element indicates the first bin edge in
the y-dimension. The second element indicates the last bin edge in
the y-dimension.
This option only bins data that falls within the bin limits inclusively,
Y>=ybmin & Y<=ybmax.
Selection mode for bin limits in y-dimension, specified as
'auto' or 'manual'. The default value is
'auto', so that the bin limits automatically adjust to the data
along the y-axis.
If you explicitly specify either YBinLimits or
YBinEdges, then YBinLimitsMode is set
automatically to 'manual'. In that case, specify
YBinLimitsMode as 'auto' to rescale the bin
limits to the data.
Binning algorithm, specified as one of the values in this table.
| Value | Description |
|---|---|
'auto' | The default |
'scott' | Scott’s rule is optimal if the data is close to being jointly
normally distributed. This rule is appropriate for most other
distributions, as well. It uses a bin size of
|
'fd' | The Freedman-Diaconis rule is less sensitive to outliers in the
data, and might be more suitable for data with heavy-tailed
distributions. It uses a bin size of
|
'integers' | The integer rule is useful with integer data, as it creates bins centered on pairs of integers. It uses a bin width of 1 for each dimension and places bin edges halfway between integers. To avoid accidentally creating too many bins, you can use this rule to create a limit of 1024 bins (210). If the data range for either dimension is greater than 1024, then the integer rule uses wider bins instead. |
histogram2adjusts the number of bins slightly so that the bin edges fall on "nice" numbers, rather than using these exact formulas.If you set the
NumBins,XBinEdges,YBinEdges,BinWidth,XBinLimits, orYBinLimitsproperties, thenBinMethodis set to'manual'.If you specify
BinMethodwithBinWidthorNumBins,histogram2only honors the last parameter.
Example: histogram2(X,Y,'BinMethod','integers')
Toggle display of empty bins, specified as either
'off' or 'on'. The default
value is 'off'.
Example: histogram2(X,Y,'ShowEmptyBins','on')
turns on the display of empty bins.
Data
Type of normalization, specified as one of the values in this table. For each
bin i:
is the bin value.
is the number of elements in the bin.
is the area of the bin, computed using the x and y bin widths.
is the number of elements in the input data. This value can be greater than the binned data if the data contains missing values or if some of the data lies outside the bin limits.
| Value | Bin Values | Notes |
|---|---|---|
'count' (default) |
|
|
'probability' |
|
|
'percentage' |
|
|
'countdensity' |
|
|
'cumcount' |
|
|
'pdf' |
|
|
'cdf' |
|
|
Example: histogram2(X,Y,'Normalization','pdf')
Color and Styling
Histogram display style, specified as either 'bar3' or
'tile'.
'bar3'— Display the histogram using 3-D bars.'tile'— Display the histogram as a rectangular array of tiles with colors indicating the bin values.
Example: histogram2(X,Y,'DisplayStyle','tile') plots the histogram
as a rectangular array of tiles.
Histogram bar color, specified as one of these values:
'none'— Bars are not filled.'flat'— Bar colors vary with height. Bars with different heights have different colors. The colors are selected from the figure or axes colormap.'auto'— Histogram bar color is chosen automatically (default).RGB triplet, hexadecimal color code, or color name — Bars are filled with the specified color.
RGB triplets and hexadecimal color codes are useful for specifying custom colors.
An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1]; for example,[0.4 0.6 0.7].A hexadecimal color code is a character vector or a string scalar that starts with a hash symbol (
#) followed by three or six hexadecimal digits, which can range from0toF. The values are not case sensitive. Thus, the color codes"#FF8800","#ff8800","#F80", and"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and hexadecimal color codes.
Color Name Short Name RGB Triplet Hexadecimal Color Code Appearance "red""r"[1 0 0]"#FF0000"
"green""g"[0 1 0]"#00FF00"
"blue""b"[0 0 1]"#0000FF"
"cyan""c"[0 1 1]"#00FFFF"
"magenta""m"[1 0 1]"#FF00FF"
"yellow""y"[1 1 0]"#FFFF00"
"black""k"[0 0 0]"#000000"
"white""w"[1 1 1]"#FFFFFF"
This table lists the default color palettes for plots in the light and dark themes.
Palette Palette Colors "gem"— Light theme defaultBefore R2025a: Most plots use these colors by default.

"glow"— Dark theme default
You can get the RGB triplets and hexadecimal color codes for these palettes using the
orderedcolorsandrgb2hexfunctions. For example, get the RGB triplets for the"gem"palette and convert them to hexadecimal color codes.RGB = orderedcolors("gem"); H = rgb2hex(RGB);Before R2023b: Get the RGB triplets using
RGB = get(groot,"FactoryAxesColorOrder").Before R2024a: Get the hexadecimal color codes using
H = compose("#%02X%02X%02X",round(RGB*255)).
If you specify DisplayStyle as 'tile', then the
FaceColor property is set to 'flat'.
Example: histogram2(X,Y,'FaceColor','g')
Histogram edge color, specified as one of these values:
'none'— Edges are not drawn.'auto'— Color of each edge is chosen automatically.RGB triplet, hexadecimal color code, or color name — Edges use the specified color.
RGB triplets and hexadecimal color codes are useful for specifying custom colors.
An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1]; for example,[0.4 0.6 0.7].A hexadecimal color code is a character vector or a string scalar that starts with a hash symbol (
#) followed by three or six hexadecimal digits, which can range from0toF. The values are not case sensitive. Thus, the color codes"#FF8800","#ff8800","#F80", and"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and hexadecimal color codes.
Color Name Short Name RGB Triplet Hexadecimal Color Code Appearance "red""r"[1 0 0]"#FF0000"
"green""g"[0 1 0]"#00FF00"
"blue""b"[0 0 1]"#0000FF"
"cyan""c"[0 1 1]"#00FFFF"
"magenta""m"[1 0 1]"#FF00FF"
"yellow""y"[1 1 0]"#FFFF00"
"black""k"[0 0 0]"#000000"
"white""w"[1 1 1]"#FFFFFF"
This table lists the default color palettes for plots in the light and dark themes.
Palette Palette Colors "gem"— Light theme defaultBefore R2025a: Most plots use these colors by default.

"glow"— Dark theme default
You can get the RGB triplets and hexadecimal color codes for these palettes using the
orderedcolorsandrgb2hexfunctions. For example, get the RGB triplets for the"gem"palette and convert them to hexadecimal color codes.RGB = orderedcolors("gem"); H = rgb2hex(RGB);Before R2023b: Get the RGB triplets using
RGB = get(groot,"FactoryAxesColorOrder").Before R2024a: Get the hexadecimal color codes using
H = compose("#%02X%02X%02X",round(RGB*255)).
Example: histogram2(X,Y,'EdgeColor','r')
Transparency of histogram bars, specified as a scalar value in range
[0,1]. histogram2 uses the
same transparency for all the bars of the histogram. A value of 1
means fully opaque and 0 means completely transparent
(invisible).
Example: histogram2(X,Y,'FaceAlpha',0.5) creates a bivariate
histogram plot with semi-transparent bars.
Transparency of histogram bar edges, specified as a scalar value in the range
[0,1]. A value of 1 means fully opaque and
0 means completely transparent (invisible).
Example: histogram2(X,Y,'EdgeAlpha',0.5) creates a bivariate
histogram plot with semi-transparent bar edges.
Lighting effect on histogram bars, specified as one of these values.
| Value | Description |
|---|---|
'lit' |
Histogram bars display a pseudo-lighting effect, where the sides of the bars use darker colors relative to the tops. The bars are unaffected by other light sources in the axes. This is the default value when |
'flat' |
Histogram bars are not lit automatically. In the presence of other light objects, the lighting effect is uniform across the bar faces. |
'none' |
Histogram bars are not lit automatically, and lights do not affect the histogram bars.
|
Example: histogram2(X,Y,'FaceLighting','none') turns off the
lighting of the histogram bars.
Line style, specified as one of the options listed in this table.
| Line Style | Description | Resulting Line |
|---|---|---|
"-" | Solid line |
|
"--" | Dashed line |
|
":" | Dotted line |
|
"-." | Dash-dotted line |
|
"none" | No line | No line |
Width of bar outlines, specified as a positive value in point units. One point equals 1/72 inch.
Example: 1.5
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Output Arguments
Bivariate histogram, returned as an object. For more information, see Histogram2 Properties.
Properties
| Histogram2 Properties | Bivariate histogram appearance and behavior |
Examples
Generate 10,000 pairs of random numbers and create a bivariate histogram. The histogram2 function automatically chooses an appropriate number of bins to cover the range of values in x and y and show the shape of the underlying distribution.
x = randn(10000,1); y = randn(10000,1); h = histogram2(x,y)
h =
Histogram2 with properties:
Data: [10000×2 double]
Values: [25×28 double]
NumBins: [25 28]
XBinEdges: [-3.9000 -3.6000 -3.3000 -3 -2.7000 -2.4000 -2.1000 -1.8000 -1.5000 -1.2000 -0.9000 -0.6000 -0.3000 0 0.3000 0.6000 0.9000 1.2000 1.5000 1.8000 2.1000 2.4000 2.7000 3.0000 3.3000 3.6000]
YBinEdges: [-4.2000 -3.9000 -3.6000 -3.3000 -3.0000 -2.7000 -2.4000 -2.1000 -1.8000 -1.5000 -1.2000 -0.9000 -0.6000 -0.3000 0 0.3000 0.6000 0.9000 1.2000 1.5000 1.8000 2.1000 2.4000 2.7000 3 3.3000 3.6000 3.9000 4.2000]
BinWidth: [0.3000 0.3000]
Normalization: 'count'
FaceColor: 'auto'
EdgeColor: [0.1294 0.1294 0.1294]
Show all properties
xlabel('x') ylabel('y')

When you specify an output argument to the histogram2 function, it returns a histogram2 object. You can use this object to inspect the properties of the histogram, such as the number of bins or the width of the bins.
Find the number of histogram bins in each dimension.
nXnY = h.NumBins
nXnY = 1×2
25 28
Plot a bivariate histogram of 1,000 pairs of random numbers sorted into 25 equally spaced bins, using 5 bins in each dimension.
x = randn(1000,1); y = randn(1000,1); nbins = 5; h = histogram2(x,y,nbins)
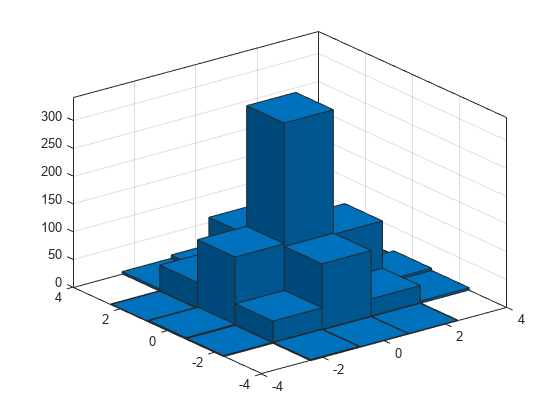
h =
Histogram2 with properties:
Data: [1000×2 double]
Values: [5×5 double]
NumBins: [5 5]
XBinEdges: [-4 -2.4000 -0.8000 0.8000 2.4000 4]
YBinEdges: [-4 -2.4000 -0.8000 0.8000 2.4000 4]
BinWidth: [1.6000 1.6000]
Normalization: 'count'
FaceColor: 'auto'
EdgeColor: [0.1294 0.1294 0.1294]
Show all properties
Find the resulting bin counts.
counts = h.Values
counts = 5×5
0 2 3 1 0
2 40 124 47 4
1 119 341 109 10
1 32 117 33 1
0 4 8 1 0
Generate 1,000 pairs of random numbers and create a bivariate histogram.
x = randn(1000,1); y = randn(1000,1); h = histogram2(x,y)

h =
Histogram2 with properties:
Data: [1000×2 double]
Values: [15×15 double]
NumBins: [15 15]
XBinEdges: [-3.5000 -3 -2.5000 -2 -1.5000 -1 -0.5000 0 0.5000 1 1.5000 2 2.5000 3 3.5000 4]
YBinEdges: [-3.5000 -3 -2.5000 -2 -1.5000 -1 -0.5000 0 0.5000 1 1.5000 2 2.5000 3 3.5000 4]
BinWidth: [0.5000 0.5000]
Normalization: 'count'
FaceColor: 'auto'
EdgeColor: [0.1294 0.1294 0.1294]
Show all properties
Use the morebins function to coarsely adjust the number of bins in the x dimension.
nbins = morebins(h,'x'); nbins = morebins(h,'x')
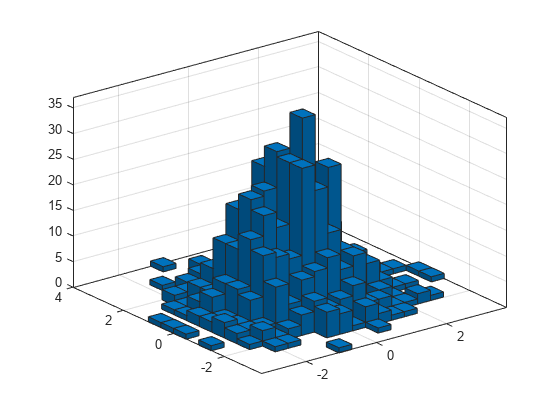
nbins = 1×2
19 15
Use the fewerbins function to adjust the number of bins in the y dimension.
nbins = fewerbins(h,'y'); nbins = fewerbins(h,'y')

nbins = 1×2
19 11
Adjust the number of bins at a fine grain level by explicitly setting the number of bins.
h.NumBins = [20 10];

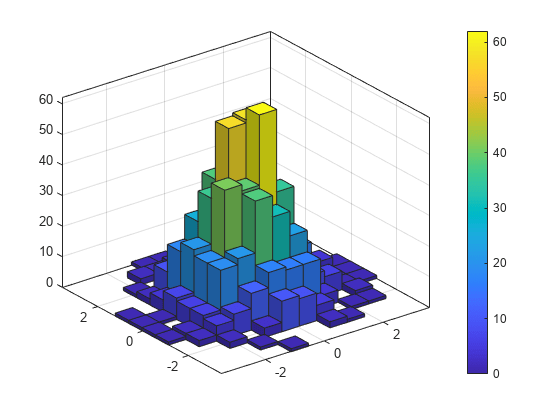
Create a bivariate histogram using 1,000 normally distributed random numbers with 12 bins in each dimension. Specify FaceColor as 'flat' to color the histogram bars by height.
h = histogram2(randn(1000,1),randn(1000,1),[12 12],'FaceColor','flat'); colorbar
Generate random data and plot a bivariate tiled histogram. Display the empty bins by specifying ShowEmptyBins as 'on'.
x = 2*randn(1000,1)+2; y = 5*randn(1000,1)+3; h = histogram2(x,y,'DisplayStyle','tile','ShowEmptyBins','on');

Generate 1,000 pairs of random numbers and create a bivariate histogram. Specify the bin edges using two vectors, with infinitely wide bins on the boundary of the histogram to capture all outliers that do not satisfy .
x = randn(1000,1); y = randn(1000,1); Xedges = [-Inf -2:0.4:2 Inf]; Yedges = [-Inf -2:0.4:2 Inf]; h = histogram2(x,y,Xedges,Yedges)

h =
Histogram2 with properties:
Data: [1000×2 double]
Values: [12×12 double]
NumBins: [12 12]
XBinEdges: [-Inf -2 -1.6000 -1.2000 -0.8000 -0.4000 0 0.4000 0.8000 1.2000 1.6000 2 Inf]
YBinEdges: [-Inf -2 -1.6000 -1.2000 -0.8000 -0.4000 0 0.4000 0.8000 1.2000 1.6000 2 Inf]
BinWidth: 'nonuniform'
Normalization: 'count'
FaceColor: 'auto'
EdgeColor: [0.1294 0.1294 0.1294]
Show all properties
When the bin edges are infinite, histogram2 displays each outlier bin (along the boundary of the histogram) as being double the width of the bin next to it.
Specify the Normalization property as 'countdensity' to remove the bins containing the outliers. Now the volume of each bin represents the frequency of observations in that interval.
h.Normalization = 'countdensity';
Generate 1,000 pairs of random numbers and create a bivariate histogram using the 'probability' normalization.
x = randn(1000,1); y = randn(1000,1); h = histogram2(x,y,'Normalization','probability')

h =
Histogram2 with properties:
Data: [1000×2 double]
Values: [15×15 double]
NumBins: [15 15]
XBinEdges: [-3.5000 -3 -2.5000 -2 -1.5000 -1 -0.5000 0 0.5000 1 1.5000 2 2.5000 3 3.5000 4]
YBinEdges: [-3.5000 -3 -2.5000 -2 -1.5000 -1 -0.5000 0 0.5000 1 1.5000 2 2.5000 3 3.5000 4]
BinWidth: [0.5000 0.5000]
Normalization: 'probability'
FaceColor: 'auto'
EdgeColor: [0.1294 0.1294 0.1294]
Show all properties
Compute the total sum of the bar heights. With this normalization, the height of each bar is equal to the probability of selecting an observation within that bin interval, and the heights of all of the bars sum to 1.
S = sum(h.Values(:))
S = 1
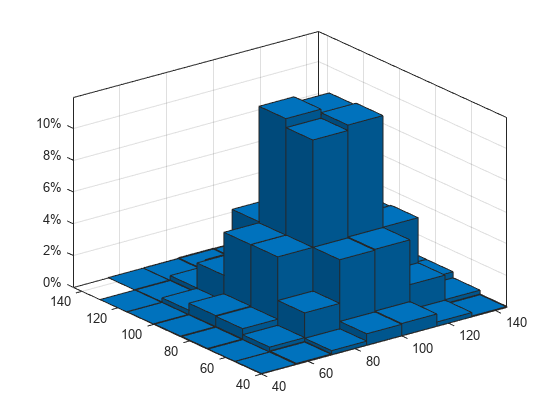
Generate 100,000 normally distributed random vectors. Use a standard deviation of 15 and means of 100 and 85.
x = [100 85] + 15*randn(1e5,2);
Plot a histogram of the random vectors. Scale and label the z-axis as percentages.
edges = 40:15:145; histogram2(x(:,1),x(:,2),edges,edges,Normalization="percentage") ztickformat("percentage")
Generate 1,000 pairs of random numbers and create a bivariate histogram. Return the histogram object to adjust the properties of the histogram without recreating the entire plot.
x = randn(1000,1); y = randn(1000,1); h = histogram2(x,y)

h =
Histogram2 with properties:
Data: [1000×2 double]
Values: [15×15 double]
NumBins: [15 15]
XBinEdges: [-3.5000 -3 -2.5000 -2 -1.5000 -1 -0.5000 0 0.5000 1 1.5000 2 2.5000 3 3.5000 4]
YBinEdges: [-3.5000 -3 -2.5000 -2 -1.5000 -1 -0.5000 0 0.5000 1 1.5000 2 2.5000 3 3.5000 4]
BinWidth: [0.5000 0.5000]
Normalization: 'count'
FaceColor: 'auto'
EdgeColor: [0.1294 0.1294 0.1294]
Show all properties
Color the histogram bars by height.
h.FaceColor = 'flat';
Change the number of bins in each direction.
h.NumBins = [10 25];
Display the histogram as a tile plot.
h.DisplayStyle = 'tile';
view(2)
Use the savefig function to save a histogram2 figure.
histogram2(randn(100,1),randn(100,1)); savefig('histogram2.fig'); close gcf
Use openfig to load the histogram figure back into MATLAB®. openfig also returns a handle to the figure, h.
h = openfig('histogram2.fig');
Use the findobj function to locate the correct object handle from the figure handle. This allows you to continue manipulating the original histogram object used to generate the figure.
y = findobj(h,'type','histogram2')
y =
Histogram2 with properties:
Data: [100×2 double]
Values: [7×6 double]
NumBins: [7 6]
XBinEdges: [-3 -2 -1 0 1 2 3 4]
YBinEdges: [-3 -2 -1 0 1 2 3]
BinWidth: [1 1]
Normalization: 'count'
FaceColor: 'auto'
EdgeColor: [0.1294 0.1294 0.1294]
Show all properties
Tips
Histogram plots created using
histogram2have a context menu in plot edit mode that enables interactive manipulations in the figure window. For example, you can use the context menu to interactively change the number of bins, align multiple histograms, or change the display order.
Extended Capabilities
This function supports tall arrays with the limitations:
Some input options are not supported. The allowed options are:
'BinWidth''XBinLimits''YBinLimits''Normalization''DisplayStyle''BinMethod'— The'auto'and'scott'bin methods are the same. The'fd'bin method is not supported.'EdgeAlpha''EdgeColor''FaceAlpha''FaceColor''LineStyle''LineWidth''Orientation'
Additionally, there is a cap on the maximum number of bars. The default maximum is 100.
The
morebinsandfewerbinsmethods are not supported.Editing properties of the histogram object that require recomputing the bins is not supported.
For more information, see Tall Arrays for Out-of-Memory Data.
Version History
Introduced in R2015bYou can create histograms with percentages on the vertical axis by setting the
Normalization name-value argument to
'percentage'.
See Also
Histogram2 Properties | bar3 | discretize | fewerbins | morebins | histcounts2 | histcounts
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)