rf.Mixer
Model RF and IQ modulator and RF and IQ demodulator with impairments and noise
Since R2024b
Description
Use the rf.Mixer
System object™ to create an idealized mixer for command line simulation. The
rf.Mixer
System object models four complex baseband mixers with impairments and noise. The four mixer
types that this System object models are modulator, demodulator, IQ modulator, and IQ
demodulator. You can also add impairments, include IQ gain, and phase mismatch where
appropriate, while noise includes both system and LO phase noise to the mixer element.
To create an idealized mixer to process complex signals:
Create the
rf.Mixerobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
rfmix = rf.Mixer
rfmix = rf.Mixer(Name=Value)rf.Mixer object using one or more name-value
arguments. For example, rfmix = rf.Mixer(Model='iqmod') creates an
idealized IQ modulator element. Properties you do not specify retain their default
values.
Properties
Unless otherwise indicated, properties are nontunable, which means you cannot change their
values after calling the object. Objects lock when you call them, and the
release function unlocks them.
If a property is tunable, you can change its value at any time.
For more information on changing property values, see System Design in MATLAB Using System Objects.
Main
Type of mixer, specified as one of the following:
mod— Modulatordemod— Demodulatoriqmod— IQ Modulatoriqdemod— IQ Demodulator
For more information, see Mixer Architectures and Design Equations (RF Blockset).
Sidebands of the mixer, specified as upper or lower.
For more information, see Mixer Sidebands (RF Blockset).
Dependencies
To enable this property, set Sideband to
mod.
Conversion gain for the mixer model, specified as a real number in dB.
RF carrier frequency for the mixer model, specified as a positive real number in Hz.
Local oscillator frequency for the mixer model, specified as a positive real number in Hz.
Impairments
LO phase offset, specified as a real number in degrees.
Dependencies
To enable this property, set Model to
mod or demod.
IQ gain imbalance, specified as a nonnegative real number in dB.
Dependencies
To enable this property, set Model to
iqmod or iqdemod.
IQ phase imbalance, specified as a real number in degrees.
Dependencies
To enable this property, set Model to
iqmod or iqdemod.
Type of third-order nonlinearity type in the cubic polynomial model, specified as
IIP3, OIP3, IP1dB,
OP1dB, IPsat, or
OPsat.
For more information, see Nonlinearities in Idealized Baseband Mixer Block (RF Blockset).
Input third-order intercept point, specified as a real positive number in dBm.
Dependencies
To enable this property, set Nonlinearity to
IIP3.
Output third-order intercept point, specified as a real positive number in dBm.
Dependencies
To enable this property, set Nonlinearity to
OIP3.
Input 1 dB compression point, specified as a real positive number in dBm.
Dependencies
To enable this property, set Nonlinearity to
IP1dB.
Output 1 dB compression point, specified as a real positive number in dBm.
Dependencies
To enable this property, set Nonlinearity to
OP1dB.
Input saturation point, specified as a real positive number in dBm.
Dependencies
To enable this property, set Nonlinearity to
IPsat.
Output saturation point, specified as a positive real number in dBm.
Dependencies
To enable this property, set Nonlinearity to
OPsat.
Mixer Noise
Options to add mixer noise to the system, specified as logical
1(true) or 0 (false).
For more information, see Mixer (System) Noise Simulations (RF Blockset).
Type of noise, specified as a noise-temperature,
NF, or noise-factor.
For more information, see Mixer (System) Noise Simulations (RF Blockset).
Dependencies
To enable this property, set IncludeNoise to 1 or
true.
Noise temperature to model the mixer noise, specified as a nonnegative real number in kelvin.
Dependencies
To enable this property, set IncludeNoiseto 1 or
true and set NoiseType to
noise-temperature.
Noise figure to model the mixer noise, specified as a nonnegative real number in dB.
Dependencies
To enable this property, set IncludeNoiseto 1 or
true and set NoiseType to
NF.
Noise factor to model mixer noise, specified as a positive integer scalar greater
than or equal to 1.
Dependencies
To enable this property, set IncludeNoise to 1 or
true and set NoiseType to
noise-factor.
Source of initial seed used to prepare the Gaussian random number noise generator, specified as one of the following:
auto— When you setNoiseSeedSourcetoauto, the object generates seeds for each mixer instance using a random number generator. The reset method of the instance has no effect.user— When you setNoiseSeedSourcetouser, the object uses the value you provide in theNoiseSeedproperty to initialize the random number generator. The reset method resets the random number generator using theNoiseSeedproperty value.
Dependencies
To enable this property, set IncludeNoise to 1 or
true.
Seed for the random number generator, specified as a nonnegative integer less than 232. Use this value to initialize the random number generator.
Dependencies
To enable this property, set IncludeNoise to 1 or
true and NoiseSeedSource to
user.
Phase Noise
Add LO phase noise to LO signal, specified as a logical 0
(false) or 1 (true).
For more information, see Phase Noise in Mixer Block (RF Blockset).
Phase noise level relative to carrier, specified as negative real scalar or vector in dBc/Hz.
Note
The number of terms specified in the PhaseNoiseLevel
property must equal the number of terms in the
PhaseNoiseFrequencyOffset property.
Dependencies
To enable this property, set IncludePhaseNoise to
1 or true.
Data Types: double
Phase frequency offset, specified as a positive real scalar or vector of positive increasing real scalar of type double in Hz.
Note
The number of terms specified in the
PhaseNoiseFrequencyOffset property must equal the number of
terms in the PhaseNoiseLevel property.
Dependencies
To enable this property, set IncludePhaseNoise to
1 or true.
Options to automatically determine number of frequency bins used in a two-sided
phase noise spectrum, specified as a logical 0 (false) or
1 (true).
You can also set the number of frequency bins using the
PhaseNoiseNumSamples and SampleRate
properties when you set the PhaseNoiseNumSamples property is set
to off.
Dependencies
To enable this property, set IncludePhaseNoise to
1 or true.
Number of samples in the time-domain signal, specified as a real nonnegative
integer less than or equal to 65536.
The value you specify here can also represent the number of frequency lines (bins)
in the signal's two-sided frequency spectrum required to achieve the frequency
resolution for the frequency offset specified in the
PhaseNoiseFrequencyOffset property.
The distance between frequency lines is
SampleRate/PhaseNoiseNumSamples. For non-positive values, the
object estimates PhaseNoiseNumSamples using the values of the
PhaseNoiseLevel and
PhaseNoiseFrequencyOffset properties. Frequency resolution
increases as the number of signal samples increases.
Note
You must set the value of this parameter to a power of 2.
Dependencies
To enable this parameter, set the IncludePhaseNoise to
1 or true parameter and set
PhaseNoiseNumSamples to 0 (false).
Source of initial seed used to prepare the Gaussian random number LO phase noise generator, specified as one of the following:
auto— When you set thePhaseNoiseSeedSourcetoauto, the object generates seeds for each mixer instance using a random number generator. The reset method of the instance has no effect.user— When you set thePhaseNoiseSeedSourcetouser, the object uses the value you provide in thePhaseNoiseSeedproperty to initialize the random number generator. The reset method resets the random number generator using thePhaseNoiseSeedproperty value.
Dependencies
To enable this property, set IncludePhaseNoise to
1 or true.
Seed for the random number generator, specified as a nonnegative integer less than 232. Use this value to initialize the random number generator.
Dependencies
To enable this property, set IncludePhaseNoise to
1 or true and PhaseNoiseSeedSource to
user.
Sample rate, specified as a nonnegative real scalar of data type double in samples per second.
Dependencies
To enable this property, set IncludePhaseNoise to
1 or true.
Usage
Syntax
Description
Input Arguments
Time-dependent input signal, specified as a real scalar, real column, complex scalar, or complex column. A column represents consecutive points in time.
Data Types: double | single
Output Arguments
Time-dependent output signal, returned as a complex scalar or complex column. The output time-dependent signal is equal in size to the input time-dependent signal.
Data Types: double | single
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
visualizePower | Plot power characteristics of idealized mixer |
visualizePhaseNoise | Plot phase noise characteristics of idealized mixer |
Examples
Create an rf.Mixer System object.
rfmix = rf.Mixer('Nonlinearity','IPsat','IPsat',30);
Generate a 16 QAM signal.
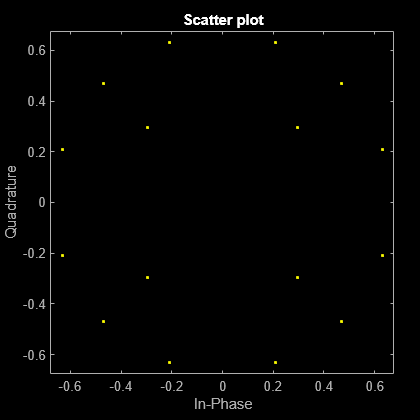
in = qammod(randi([0 15],1000,1),16,'UnitAveragePower',true);Apply the cubic nonlinearity mixer model to the16 QAM signal and plot the results.
out = rfmix(in); scatterplot(out)
Define modulation order, samples per symbol, and input power.
M = 16; sps = 4; pindBm = 0;
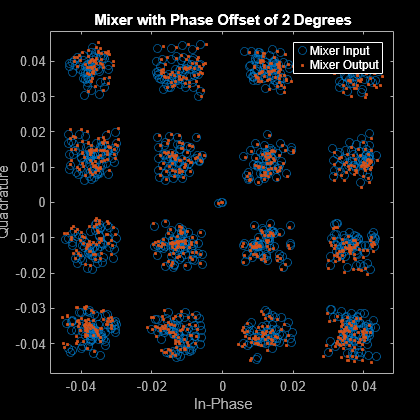
Create an idealized baseband mixer element with the phase offset of 2 degrees.
rfMixer = rf.Mixer('PhaseOffset',2);Apply pulse shaping by interpolating an input signal using a raised cosine finite impulse response (FIR) filter.
txfilter = comm.RaisedCosineTransmitFilter('RolloffFactor',0.9, 'FilterSpanInSymbols',6, ... 'OutputSamplesPerSymbol',sps,'Gain',sqrt(sps));
Define the input signal.
pin = 10.^((pindBm-30)/10); % Unit: W
data = randi([0 M-1],1000,1);Define the modulated, filtered, and mixer signals.
modSignal = qammod(data,M,'UnitAveragePower',true)*sqrt(pin);
filterSignal = txfilter(modSignal);
mixerSignal = rfMixer(filterSignal);Plot the mixer characteristics with a phase offset of 2 degrees.
scatFig = scatterplot(filterSignal,sps,0,'o'); hold on scatterplot(mixerSignal,sps,0,'.',scatFig) legend({'Mixer Input' 'Mixer Output'},'Location','northeast') title('Mixer with Phase Offset of 2 Degrees')
This example shows how to input a two-tone signal to an idealized system. To design this RF system:
First, generate a two-tone source.
Second, connect this two-tone source to an idealized RF PA.
Finally, observe the output response of this system.
Introduction
The RF system designed in this example uses the Idealized Baseband System object™ to analyze a cascade of mathematical models of RF components within the MATLAB® environment. During analysis, these System objects uses complex-baseband representation of the RF elements to compute time-domain waveforms. These complex modulated signals represent the transmitted information, assumed to be centered around an implicit carrier frequency. The models from the Idealized Baseband library do not model out-of-band behavior or spurious harmonics generated by nonlinear effects or interfering signals. Additionally, models from the Idealized Baseband library do not model impedance mismatches and assume that all blocks are perfectly matched. As a result, RF models built with the Idealized Baseband library simulate rapidly.
Create Two-Tone Source Generator
This figure shows the architecture of a two-tone source generator. This generator consists of a sine wave generator that produces two sinusoidal signals. These signals are multiplied by a -40 dB gain and then processed by a summer.

Define sample rate and samples per frame of the sine wave signals.
sampleRate = 1/2e-8; samplesPerFrame = 512;
Define a gain of - 40 dB.
m40dB = 10^(-40/20); % Request Jeff: Why -40 dB?Create two sinusoid signals at 1.8 GHz and 2.6 GHz.
SineObj1 = dsp.SineWave('Frequency',1.8e6,'SampleRate',sampleRate, ... SamplesPerFrame=samplesPerFrame,ComplexOutput=true); SineObj2 = dsp.SineWave('Frequency',2.6e6,'SampleRate',sampleRate, ... SamplesPerFrame=samplesPerFrame,ComplexOutput=true);
Display the spectral analysis of a two tone signal source, where each tone is -10 dBm.
SpectAnal = spectrumAnalyzer('SampleRate',sampleRate,'ShowLegend',true); for Iter = 1:10 sineWave1 = SineObj1(); sineWave2 = SineObj2(); sigIn = m40dB*(sineWave1 + sineWave2); SpectAnal(sigIn); end

Simulate Idealized System
This figure shows how to create a system to IQ modulate the two-tone signal and amplify using an RF PA. The system architecture involves connecting a cubic polynomial amplifier to an IQ modulator. The output from the IQ modulator is then connected to a cross-term (CT) memory power amplifier. A two-tone signal is supplied as input to the system, and the output is connected to a spectrum analyzer for visualizing the power amplifier characteristics.

Load the pre-computed PA coefficient matrix.
load('PAcoefficients_rf.mat','fitCoefMat')
Create an idealized baseband cubic polynomial amplifier and IQ modulator with nonlinearity and noise.
preAmpIQ = rf.Amplifier('Gain',8,'Nonlinearity','IIP3','IIP3',45, ... 'IncludeNoise',true,NF=1.5); mixerModIQ = rf.Mixer('Model','iqmod','Gain',0,'LO',1e8, ... 'PhaseImbalance',.5,'Nonlinearity','IIP3',IIP3=50, ... IncludeNoise=true,NoiseType='NF',NF=6);
Create an idealized baseband cross-term memory PA.
powerAmp = rf.PAmemory('Model','Cross-term memory', ... 'CoefficientMatrix','fitCoefMat');
Connect the RF chain and provide the two-tone signal as input.
SpectAnal = spectrumAnalyzer('SampleRate',sampleRate,'ShowLegend',true); for Iter = 1:10 sineWave1 = SineObj1(); sineWave2 = SineObj2(); sineIn = m40dB*(sineWave1 + sineWave2); ampIQ = preAmpIQ(sineIn); modIQ = mixerModIQ(ampIQ); paOut = powerAmp(modIQ*sqrt(50))/sqrt(50); SpectAnal(paOut); end

References
[1] Razavi, Behzad. “Basic Concepts “ in RF Microelectronics, 2nd edition, Prentice Hall, 2012.
[2] Kundert, Ken.“ Accurate and Rapid Measurement of IP2 and IP3,“ The Designer Guide Community, May 22, 2002.
[3] Kasdin, N.J. “Discrete Simulation of Colored Noise and Stochastic Processes and 1/f α Power Law Noise Generation.” Proceedings of the IEEE 83, no. 5 (May 1995): 802–27. https://doi.org/10.1109/5.381848.
Version History
Introduced in R2024b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)