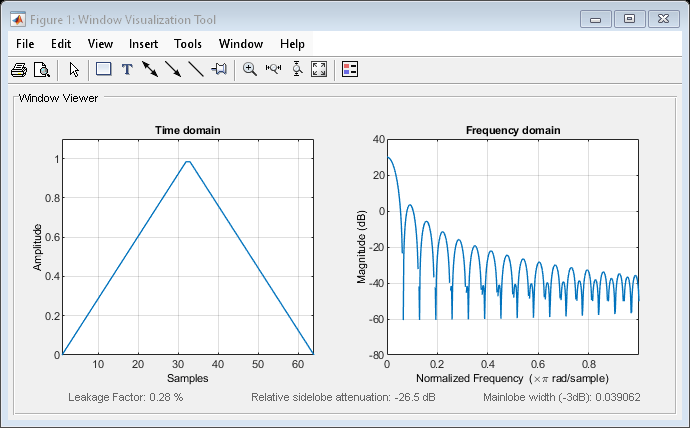
bartlett
Bartlett window
Description
Examples
Input Arguments
Output Arguments
Algorithms
The following equation generates the coefficients of a Bartlett window:
The window length .
The Bartlett window is very similar to a triangular window as returned by the triang function. However, the Bartlett window always has zeros at the first and
last samples, while the triangular window is nonzero at those points. For odd values of
L, the center L-2 points of
bartlett(L) are equivalent to triang(L-2).
Note
If you specify a one-point window (L = 1), the
value 1 is returned.
References
[1] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice Hall, 1999, pp.
Extended Capabilities
Version History
Introduced before R2006aSee Also
Apps
Functions
barthannwin|blackmanharris|bohmanwin|nuttallwin|parzenwin|rectwin|triang| WVTool