isminphase
Determine whether filter is minimum phase
Syntax
Description
flag = isminphase(B,A,"ctf")1 if the filter specified as Cascaded Transfer Functions (CTF) with numerator coefficients B and denominator coefficients
A is minimum phase. (since R2024b)
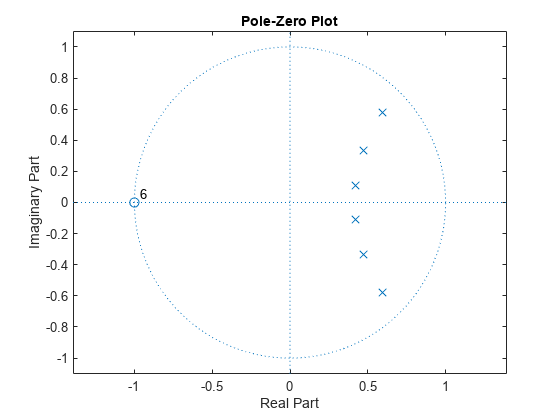
flag = isminphase(d)1 if the digital filter d is minimum phase.
Use designfilt to generate d
based on frequency-response specifications.
Examples
Input Arguments
Output Arguments
More About
Tips
References
[1] Lyons, Richard G. Understanding Digital Signal Processing. Upper Saddle River, NJ: Prentice Hall, 2004.
Version History
Introduced in R2013aSee Also
ctffilt | designfilt | digitalFilter | isallpass | islinphase | ismaxphase | isstable