boxplot

Visualize summary statistics with box plot

Syntax

boxplot(x)

boxplot(x,g)

boxplot(ax,___)

boxplot(___,Name,Value)

Description

boxplot(x) creates a box plot of the data in x. If x is a vector, boxplot plots one box. If x is a matrix, boxplot plots one box for each column of x.

On each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points not considered outliers, and the outliers are plotted individually using the '+' symbol.

boxplot(x,g) creates a box plot using one or more grouping variables contained in g. boxplot produces a separate box for each set of x values that share the same g value or values.

boxplot(ax,___) creates a box plot using the axes specified by the axes graphic object ax, using any of the previous syntaxes.

boxplot(___,Name,Value) creates a box plot with additional options specified by one or more Name,Value pair arguments. For example, you can specify the box style or order.

Examples

Create a Box Plot

Load the sample data.

load carsmall

Create a box plot of the miles per gallon (MPG) measurements. Add a title and label the axes.

boxplot(MPG)
xlabel('All Vehicles')
ylabel('Miles per Gallon (MPG)')
title('Miles per Gallon for All Vehicles')

The boxplot shows that the median miles per gallon for all vehicles in the sample data is approximately 24. The minimum value is about 9, and the maximum value is about 44.

Create Box Plots for Grouped Data

Load the sample data.

load carsmall

Create a box plot of the miles per gallon (MPG) measurements from the sample data, grouped by the vehicles' country of origin (Origin). Add a title and label the axes.

boxplot(MPG,Origin)
title('Miles per Gallon by Vehicle Origin')
xlabel('Country of Origin')
ylabel('Miles per Gallon (MPG)')

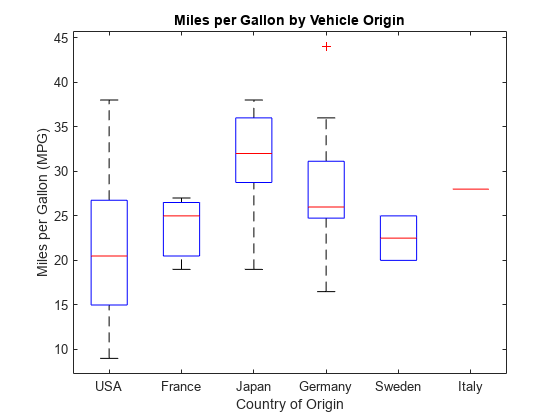
Each box visually represents the MPG data for cars from the specified country. Italy's "box" appears as a single line because the sample data contains only one observation for this group.

Create Notched Box Plots

Generate two sets of sample data. The first sample, x1, contains random numbers generated from a normal distribution with mu = 5 and sigma = 1. The second sample, x2, contains random numbers generated from a normal distribution with mu = 6 and sigma = 1.

rng default  % For reproducibility
x1 = normrnd(5,1,100,1);
x2 = normrnd(6,1,100,1);

Create notched box plots of x1 and x2. Label each box with its corresponding mu value.

figure
boxplot([x1,x2],'Notch','on','Labels',{'mu = 5','mu = 6'})
title('Compare Random Data from Different Distributions')

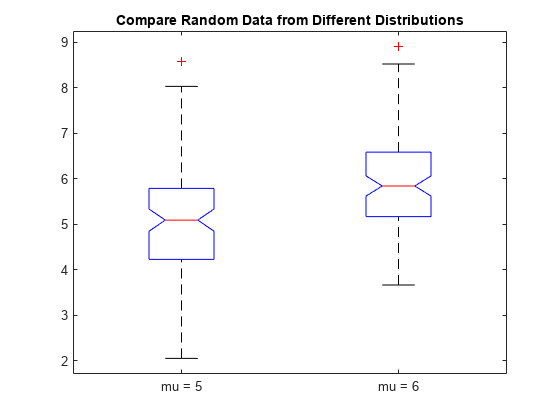
The boxplot shows that the difference between the medians of the two groups is approximately 1. Since the notches in the box plot do not overlap, you can conclude, with 95% confidence, that the true medians do differ.

The following figure shows the box plot for the same data with the maximum whisker length specified as 1.0 times the interquartile range. Data points beyond the whiskers are displayed using +.

figure
boxplot([x1,x2],'Notch','on','Labels',{'mu = 5','mu = 6'},'Whisker',1)
title('Compare Random Data from Different Distributions')

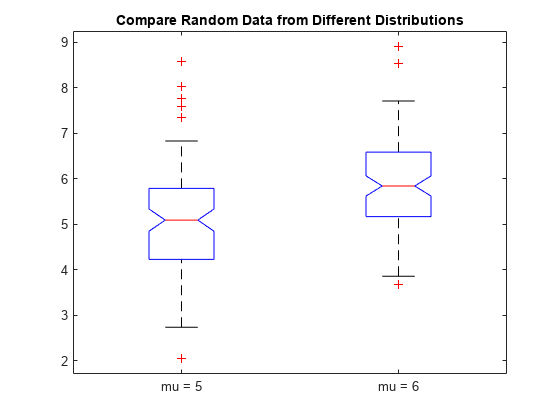
With the smaller whiskers, boxplot displays more data points as outliers.

Create Compact Box Plots

Create a 100-by-25 matrix of random numbers generated from a standard normal distribution to use as sample data.

rng default  % For reproducibility
x = randn(100,25);

Create two box plots for the data in x on the same figure. Use the default formatting for the top plot, and compact formatting for the bottom plot.

figure

subplot(2,1,1)
boxplot(x)

subplot(2,1,2)
boxplot(x,'PlotStyle','compact')

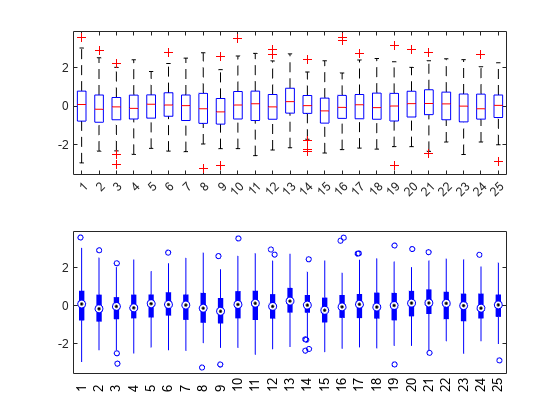
Each plot presents the same data, but the compact formatting may improve readability for plots with many boxes.

Box Plots for Vectors of Varying Length

Create box plots for data vectors of varying length by using a grouping variable.

Randomly generate three column vectors of varying length: one of length 5, one of length 10, and one of length 15. Combine the data into a single column vector of length 30.

rng('default')  % For reproducibility
x1 = rand(5,1);
x2 = rand(10,1);
x3 = rand(15,1);
x = [x1; x2; x3];

Create a grouping variable that assigns the same value to rows that correspond to the same vector in x. For example, the first five rows of g have the same value, First, because the first five rows of x all come from the same vector, x1.

g1 = repmat({'First'},5,1);
g2 = repmat({'Second'},10,1);
g3 = repmat({'Third'},15,1);
g = [g1; g2; g3];

Create the box plots.

boxplot(x,g)

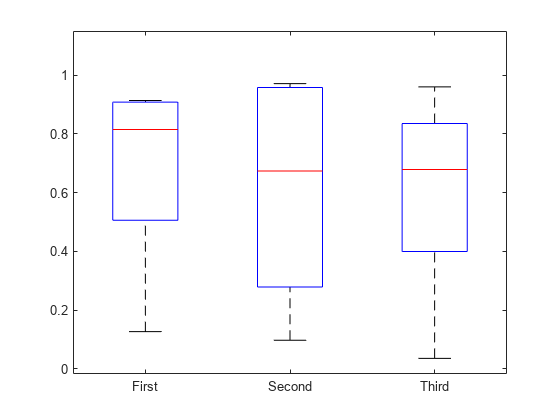
Input Arguments

x — Input data

numeric vector | numeric matrix

Input data, specified as a numeric vector or numeric matrix. If x is a vector, boxplot plots one box. If x is a matrix, boxplot plots one box for each column of x.

On each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points not considered outliers, and the outliers are plotted individually using the '+' symbol.

Data Types: single | double

g — Grouping variables

numeric vector | character array | string array | cell array | categorical array

Grouping variables, specified as a numeric vector, character array, string array, cell array, or categorical array. You can specify multiple grouping variables in g by using a cell array of these variable types or a matrix. If you specify multiple grouping variables, they must all be the same length.

If x is a vector, then the grouping variables must contain one row for each element of x. If x is a matrix, then the grouping variables must contain one row for each column of x. Groups that contain a missing value (NaN), an empty character vector, an empty or <missing> string, or an <undefined> value in a grouping variable are omitted, and are not counted in the number of groups considered by other parameters.

By default, boxplot sorts character and string grouping variables in the order they initially appear in the data, categorical grouping variables by the order of their levels, and numeric grouping variables in numeric order. To control the order of groups, do one of the following:

• Use categorical variables in g and specify the order of their levels.

• Use the 'GroupOrder' name-value pair argument.

• Pre-sort your data.

Data Types: single | double | char | string | cell | categorical

ax — Axes on which to plot

axes graphic object

Axes on which to plot, specified as an axes graphic object. If you do not specify ax, then boxplot creates the plot using the current axis. For more information on creating an axes graphic object, see axes and Axes Properties.

Name-Value Pair Arguments

Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside quotes. You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

Example: 'Notch','on','Labels',{'mu = 5','mu = 6'} creates a notched box plot and labels the two boxes mu = 5 and mu = 6, from left to right

Box Appearance

'BoxStyle' — Box style

'outline' | 'filled'

Box style, specified as the comma-separated pair consisting of 'BoxStyle' and one of the following.

Name	Value
'outline'	Plot boxes using an unfilled box with dashed whiskers. This is the default if 'PlotStyle' is 'traditional'.
'filled'	Plot boxes using a narrow filled box with lines for whiskers. This is the default if 'PlotStyle' is 'compact'.

Example: 'BoxStyle','filled'

'Colors' — Box colors

RGB triplet | character vector or string scalar of color names

Box colors, specified as the comma-separated pair consisting of 'Colors' and an RGB triplet, character vector, or string scalar. An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color, respectively. Each intensity must be in the range [0,1].

The following table lists the available color characters and their equivalent RGB triplet values.

Long Name	Short Name	RGB Triplet
Yellow	'y'	[1 1 0]
Magenta	'm'	[1 0 1]
Cyan	'c'	[0 1 1]
Red	'r'	[1 0 0]
Green	'g'	[0 1 0]
Blue	'b'	[0 0 1]
White	'w'	[1 1 1]
Black	'k'	[0 0 0]

You can specify multiple colors either as a character vector or string scalar of color names (for example, 'rgbm') or a three-column matrix of RGB values. The sequence is replicated or truncated as required, so for example, 'rb' gives boxes that alternate red and blue.

If you do not specify the name-value pair 'ColorGroup', then boxplot uses the same color scheme for all boxes. If you do specify 'ColorGroup', then the default is a modified hsv colormap.

Example: 'Colors','rgbm'

'MedianStyle' — Median style

'line' | 'target'

Median style, specified as the comma-separated pair consisting of 'MedianStyle' and one of the following.

Name	Value
'line'	Draw a line to represent the median in each box. This is the default when 'PlotStyle' is 'traditional'.
'target'	Draw a black dot inside a white circle to represent the median in each box. This is the default when 'PlotStyle' is 'compact'.

Example: 'MedianStyle','target'

'Notch' — Marker for comparison intervals

'off' (default) | 'on' | 'marker'

Marker for comparison intervals, specified as the comma-separated pair consisting of 'Notch' and one of the following.

Name	Value
'off'	Omit comparison intervals from box display.
'on'	If 'PlotStyle' is 'traditional', draw comparison intervals using notches. If 'PlotStyle' is 'compact', draw comparison intervals using triangular markers.
'marker'	Draw comparison intervals using triangular markers.

Two medians are significantly different at the 5% significance level if their intervals do not overlap. boxplot represents interval endpoints using the extremes of the notches or the centers of the triangular markers. The notch extremes correspond to q₂ – 1.57(q₃ – q₁)/sqrt(n) and q₂ + 1.57(q₃ – q₁)/sqrt(n), where q₂ is the median (50th percentile), q₁ and q₃ are the 25th and 75th percentiles, respectively, and n is the number of observations without any NaN values. If the sample size is small, the notches might extend beyond the end of the box.

Example: 'Notch','on'

'OutlierSize' — Marker size for outliers

positive numeric value

Marker size for outliers, specified as the comma-separated pair consisting of 'OutlierSize' and a positive numeric value. The specified value represents the marker size in points.

If 'PlotStyle' is 'traditional', then the default value for OutlierSize is 6. If 'PlotStyle' is 'compact', then the default value for OutlierSize is 4.

Example: 'OutlierSize',8

Data Types: single | double

'PlotStyle' — Plot style

'traditional' (default) | 'compact'

Plot style, specified as the comma-separated pair consisting of 'PlotStyle' and one of the following.

Name	Value
'traditional'	Plot boxes using a traditional box style.
'compact'	Plot boxes using a smaller box style designed for plots with many groups. This style changes the defaults for some other parameters.

Example: 'PlotStyle','compact'

'Symbol' — Symbol and color for outliers

line specification

Symbol and color for outliers, specified as the comma-separated pair consisting of 'Symbol' and a line specification. See the LineSpec parameter in plot for available line specifications.

If 'PlotStyle' is 'traditional', then the default value is 'r+', which plots each outlier using a red '+' symbol.

If 'PlotStyle' is 'compact', then the default value is 'o', which plots each outlier using an 'o' symbol in the same color as the corresponding box.

If you omit the symbol, then the outliers appear invisible. If you omit the color, then the outliers appear in the same color as the box.

Example: 'kx'

'Widths' — Box width

numeric scalar | numeric vector

Box width, specified as the comma-separated pair consisting of 'Widths' and a numeric scalar or numeric vector. If the number of boxes is not equal to the number of width values specified, then the list of values is replicated or truncated as necessary.

This name-value pair argument does not alter the spacing between boxes. Therefore, if you specify a large value for 'Widths', the boxes might overlap.

The default box width is equal to half of the minimum separation between boxes, which is 0.5 when the 'Positions' name-value pair argument takes its default value.

Example: 'Widths',0.3

Data Types: single | double

Group Appearance

'ColorGroup' — Grouping variable for box color change

[] (default) | numeric vector | character array | string array | cell array | categorical array

Grouping variable for box color change, specified as the comma-separated pair consisting of 'ColorGroup' and a grouping variable. The grouping variable is a numeric vector, character array, string array, cell array, or categorical array. The box color changes when the specified grouping variable changes. The default value [] indicates that the box color does not change based on the group.

Data Types: single | double | char | string | cell | categorical

'FactorDirection' — Order of factors on plot

'data' (default) | 'list' | 'auto'

Order of factors on plot, specified as the comma-separated pair consisting of 'FactorDirection' and one of the following.

Name	Value
'data'	Factors appear with the first value next to the plot origin.
'list'	Factors appear left-to-right if on the x-axis, or top-to-bottom if on the y-axis.
'auto'	If the grouping variables are numeric, then boxplot uses 'data'. If the grouping variables are character arrays, string arrays, cell arrays, or categorical arrays, then boxplot uses 'list'.

'FullFactors' — Plot all group factors

'off' (default) | 'on'

Plot all group factors, specified as the comma-separated pair consisting of 'FullFactors' and either 'off' or 'on'. If 'off', then boxplot plots one box for each unique row of grouping variables. If 'on', then boxplot plots one box for each possible combination of grouping variable values, including combinations that do not appear in the data.

Example: 'FullFactors','on'

'FactorGap' — Distance between different grouping factors

[] | positive numeric value | vector of positive numeric values | 'auto'

Distance between different grouping factors, specified as the comma-separated pair consisting of 'FactorGap' and a positive numeric value, a vector of positive numeric values, or 'auto'. If you specify a vector, then the vector length must be less than or equal to the number of grouping variables.

'FactorGap' represents the distance of the gap between different factors of a grouping variable, expressed as a percentage of the width of the plot. For example, if you specify [3,1], then the gap is three percent of the width of the plot between groups with different values of the first grouping variable, and one percent between groups with the same value of the first grouping variable but different values for the second.

If you specify 'auto', then boxplot selects a gap distance automatically. The value [] indicates no change in gap size between different factors.

If 'PlotStyle' is 'traditional', then the default value for FactorGap is []. If 'PlotStyle' is 'compact', then the default value is 'auto'.

Example: 'FactorGap',[3,1]

Data Types: single | double | char | string

'FactorSeparator' — Separation between grouping factors

[] | positive integer | vector of positive integers | 'auto'

Separation between grouping factors, specified as the comma-separated pair consisting of 'FactorSeparator' and a positive integer or a vector of positive integers, or 'auto'. If you specify a vector, then the length of the vector should be less than or equal to the number of grouping variables. The integer values must be in the range [1,G], where G is the number of grouping variables.

'FactorSeparator' specifies which factors should have their values separated by a grid line. For example, [1,2] adds a separator line when the first or second grouping variable changes value.

If 'PlotStyle' is 'traditional', then the default value for FactorSeparator is []. If 'PlotStyle' is 'compact', then the default value is 'auto'.

Example: 'FactorSeparator',[1,2]

Data Types: single | double | char | string

'GroupOrder' — Plotting order of groups

[] (default) | string array | cell array

Plotting order of groups, specified as the comma-separated pair consisting of 'GroupOrder' and a string array or cell array containing the names of the grouping variables. If you have multiple grouping variables, separate values with a comma. You can also use categorical arrays as grouping variables to control the order of the boxes. The default value [] does not reorder the boxes.

Data Types: string | cell

Data Limits and Maximum Distances

'DataLim' — Extreme data limits

[-Inf,Inf] (default) | two-element numeric vector

Extreme data limits, specified as the comma-separated pair consisting of 'DataLim' and a two-element numeric vector containing the lower and upper limits, respectively. The values specified for 'DataLim' are used by 'ExtremeMode' to determine which data points are extreme.

Data Types: single | double

'ExtremeMode' — Handling method for extreme data

'clip' (default) | 'compress'

Handling method for extreme data, specified as the comma-separated pair consisting of 'ExtremeMode' and one of the following.

Name	Value
'clip'	If any data values fall outside the limits specified by 'DataLim', then boxplot displays these values at DataLim on the plot.
'compress'	If any data values fall outside the limits specified by 'DataLim' , then boxplot displays these values evenly distributed in a region just outside DataLim, retaining the relative order of the points.

If any data points lie outside the limit specified by 'DataLim', then the limit is marked with a dotted line. If any data points are compressed, then two gray lines mark the compression region. Values at –Inf or Inf can be clipped or compressed, but NaN values do not appear on the plot. Box notches are drawn to scale and may extend beyond the bounds if the median is inside the limit. Box notches are not drawn if the median is outside the limits.

Example: 'ExtremeMode','compress'

'Jitter' — Maximum outlier displacement distance

numeric value

Maximum outlier displacement distance, specified as the comma-separated pair consisting of 'Jitter' and a numeric value. Jitter is the maximum distance to displace outliers along the factor axis by a uniform random amount, in order to make duplicate points visible. If you specify 'Jitter' equal to 1, then the jitter regions just touch between the closest adjacent groups.

If 'PlotStyle' is 'traditional', then the default value for Jitter is 0. If 'PlotStyle' is 'compact', then the default value is 0.5.

Example: 'Jitter',1

Data Types: single | double

'Whisker' — Multiplier for maximum whisker length

1.5 (default) | positive numeric value

Multiplier for the maximum whisker length, specified as the comma-separated pair consisting of 'Whisker' and a positive numeric value. The maximum whisker length is the product of Whisker and the interquartile range.

boxplot draws points as outliers if they are greater than q₃ + w × (q₃ – q₁) or less than q₁ – w × (q₃ – q₁), where w is the multiplier Whisker, and q₁ and q₃ are the 25th and 75th percentiles of the sample data, respectively.

The default value for 'Whisker' corresponds to approximately +/–2.7σ and 99.3 percent coverage if the data are normally distributed. The plotted whisker extends to the adjacent value, which is the most extreme data value that is not an outlier.

Specify 'Whisker' as 0 to give no whiskers and to make every point outside of q₁ and q₃ an outlier.

Example: 'Whisker',0

Data Types: single | double

Plot Appearance

'Labels' — Box labels

character array | string array | cell array | numeric vector | numeric matrix

Box labels, specified as the comma-separated pair consisting of 'Labels' and a character array, string array, cell array, or numeric vector containing the box label names. Specify one label per x value or one label per group. To specify multiple label variables, use a numeric matrix or a cell array containing any of the accepted data types.

To remove labels from a plot , use the following command: set(gca,'XTickLabel',{' '}).

Data Types: char | string | cell | single | double

'LabelOrientation' — Label orientation

'inline' | 'horizontal'

Label orientation, specified as the comma-separated pair consisting of 'LabelOrientation' and one of the following.

Name	Value
'inline'	Rotate box labels to be vertical. This is the default when 'PlotStyle' is 'compact'.
'horizontal'	Leave box labels horizontal. This is the default when 'PlotStyle' is 'traditional'.

If the labels are on the y axis, then both settings leave the labels horizontal.

Example: 'LabelOrientation','inline'

'LabelVerbosity' — Labels to display on plot

'all' | 'minor' | 'majorminor'

Labels to display on plot, specified as the comma-separated pair consisting of 'LabelVerbosity' and one of the following.

Name	Value
'all'	Display a label for every value of a grouping variable. This is the default when 'PlotStyle' is 'traditional'.
'minor'	For any grouping variable, display the value corresponding to box j only if that value differs from the value corresponding to box (j – 1).
'majorminor'	For any grouping variable g(:,i), display the value corresponding to box j, only if that value differs from the value of g(:,i) corresponding to box (j – 1), or if the condition above holds for at least one of the grouping variables g(:,1),…,g(:,i-1). This is the default when 'PlotStyle' is 'compact'.

Example: 'LabelVerbosity','minor'

'Orientation' — Plot orientation

'vertical' (default) | 'horizontal'

Plot orientation, specified as the comma-separated pair consisting of 'Orientation' and one of the following.

Name	Value
'vertical'	Plot x on the y-axis.
'horizontal'	Plot x on the x-axis.

Example: 'horizontal'

'Positions' — Box positions

numeric vector

Box positions, specified as the comma-separated pair consisting of 'Positions' and a numeric vector containing one entry for each group or x value. The default is 1:NumGroups, where NumGroups is the number of groups.

Data Types: single | double

More About

Box Plot

A box plot provides a visualization of summary statistics for sample data and contains the following features:

• The bottom and top of each box are the 25th and 75th percentiles of the sample, respectively. The distance between the bottom and top of each box is the interquartile range.

• The red line in the middle of each box is the sample median. If the median is not centered in the box, the plot shows sample skewness.

• The whiskers are lines extending above and below each box. Whiskers go from the end of the interquartile range to the furthest observation within the whisker length (the adjacent value).

• Observations beyond the whisker length are marked as outliers. By default, an outlier is a value that is more than 1.5 times the interquartile range away from the bottom or top of the box. However, you can adjust this value by using additional input arguments. An outlier appears as a red + sign.

• Notches display the variability of the median between samples. The width of a notch is computed so that boxes whose notches do not overlap have different medians at the 5% significance level. The significance level is based on a normal distribution assumption, but comparisons of medians are reasonably robust for other distributions. Comparing box plot medians is like a visual hypothesis test, analogous to the t test used for means.

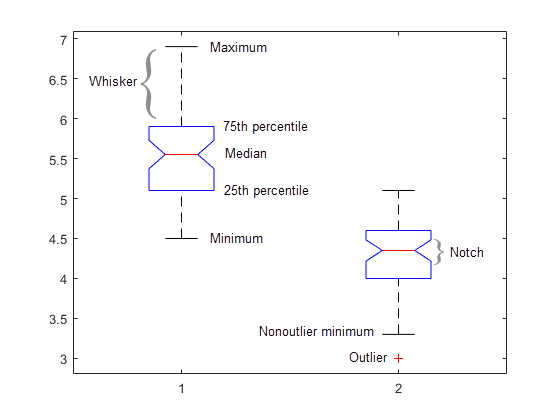
Tips

• boxplot creates a visual representation of the data, but does not return numeric values. To calculate the relevant summary statistics for the sample data, use the following functions:

  • min — Find the minimum value in the sample data.

  • max — Find the maximum value in the sample data.

  • median — Find the median value in the sample data.

  • quantile — Find the quantile values in the sample data. For example, to compute the 25th and 75th percentiles of x, specify quantile(x,[0.25 0.75]). For more information on how the percentiles are computed, see Algorithms.

  • iqr — Find the interquartile range in the sample data.

  • grpstats — Calculate summary statistics for the sample data, organized by group.

• You can see data values and group names using the data cursor in the figure window. The cursor shows the original values of any points affected by the datalim parameter. You can label the group to which an outlier belongs using the gname function.

• To modify graphics properties of a box plot component, use findobj with the Tag property to find the component's handle. Tag values for box plot components depend on parameter settings, and are listed in the following table.

  Parameter Settings	Tag Values
  All settings	'Box' 'Outliers'
  When 'PlotStyle' is 'traditional'	'Median' 'Upper Whisker' 'Lower Whisker' 'Upper Adjacent Value' 'Lower Adjacent Value'
  When 'PlotStyle' is 'compact'	'Whisker' 'MedianOuter' 'MedianInner'
  When 'Notch' is 'marker'	'NotchLo' 'NotchHi'

Alternative Functionality

You can also create a BoxChart object by using the boxchart function. Although boxchart does not include all the functionality of boxplot, it has some advantages. Unlike boxplot, the boxchart function:

• Allows for categorical rulers along the group axis

• Provides the option of a legend

• Works well with the hold on command

• Has an improved visual design that helps you see notches more easily

To control the appearance and behavior of the object, change the BoxChart Properties.

References

[1] McGill, R., J. W. Tukey, and W. A. Larsen. “Variations of Boxplots.” The American Statistician. Vol. 32, No. 1, 1978, pp. 12–16.

[2] Velleman, P.F., and D.C. Hoaglin. Applications, Basics, and Computing of Exploratory Data Analysis. Pacific Grove, CA: Duxbury Press, 1981.

[3] Nelson, L. S. “Evaluating Overlapping Confidence Intervals.” Journal of Quality Technology. Vol. 21, 1989, pp. 140–141.

[4] Langford, E. “Quartiles in Elementary Statistics”, Journal of Statistics Education. Vol. 14, No. 3, 2006.