kfoldMargin

Classification margins for cross-validated linear classification model

Syntax

m = kfoldMargin(CVMdl)

Description

m = kfoldMargin(CVMdl) returns the cross-validated classification margins obtained by the cross-validated, binary, linear classification model CVMdl. That is, for every fold, kfoldMargin estimates the classification margins for observations that it holds out when it trains using all other observations.

m contains classification margins for each regularization strength in the linear classification models that comprise CVMdl.

Examples

Estimate k-Fold Cross-Validation Margins

Load the NLP data set.

load nlpdata

X is a sparse matrix of predictor data, and Y is a categorical vector of class labels. There are more than two classes in the data.

The models should identify whether the word counts in a web page are from the Statistics and Machine Learning Toolbox™ documentation. So, identify the labels that correspond to the Statistics and Machine Learning Toolbox™ documentation web pages.

Ystats = Y == 'stats';

Cross-validate a binary, linear classification model that can identify whether the word counts in a documentation web page are from the Statistics and Machine Learning Toolbox™ documentation.

rng(1); % For reproducibility 
CVMdl = fitclinear(X,Ystats,'CrossVal','on');

CVMdl is a ClassificationPartitionedLinear model. By default, the software implements 10-fold cross validation. You can alter the number of folds using the 'KFold' name-value pair argument.

Estimate the cross-validated margins.

m = kfoldMargin(CVMdl);
size(m)

ans = 1×2

       31572           1

m is a 31572-by-1 vector. m(j) is the average of the out-of-fold margins for observation j.

Plot the k-fold margins using box plots.

figure;
boxplot(m);
h = gca;
h.YLim = [-5 30];
title('Distribution of Cross-Validated Margins')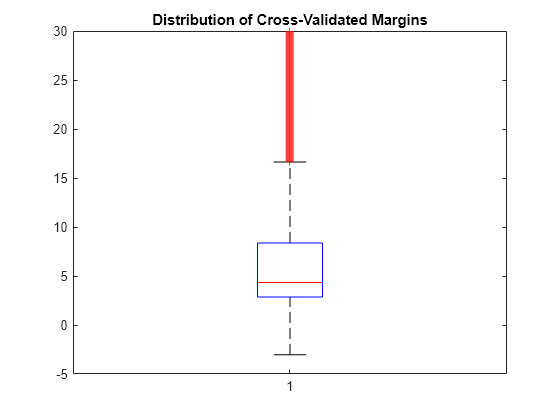

Feature Selection Using k-fold Margins

One way to perform feature selection is to compare k-fold margins from multiple models. Based solely on this criterion, the classifier with the larger margins is the better classifier.

Load the NLP data set. Preprocess the data as in Estimate k-Fold Cross-Validation Margins.

load nlpdata
Ystats = Y == 'stats';
X = X';

Create these two data sets:

• fullX contains all predictors.

• partX contains 1/2 of the predictors chosen at random.

rng(1); % For reproducibility
p = size(X,1); % Number of predictors
halfPredIdx = randsample(p,ceil(0.5*p));
fullX = X;
partX = X(halfPredIdx,:);

Cross-validate two binary, linear classification models: one that uses the all of the predictors and one that uses half of the predictors. Optimize the objective function using SpaRSA, and indicate that observations correspond to columns.

CVMdl = fitclinear(fullX,Ystats,'CrossVal','on','Solver','sparsa',...
    'ObservationsIn','columns');
PCVMdl = fitclinear(partX,Ystats,'CrossVal','on','Solver','sparsa',...
    'ObservationsIn','columns');

CVMdl and PCVMdl are ClassificationPartitionedLinear models.

Estimate the k-fold margins for each classifier. Plot the distribution of the k-fold margins sets using box plots.

fullMargins = kfoldMargin(CVMdl);
partMargins = kfoldMargin(PCVMdl);

figure;
boxplot([fullMargins partMargins],'Labels',...
    {'All Predictors','Half of the Predictors'});
h = gca;
h.YLim = [-30 60];
title('Distribution of Cross-Validated Margins')

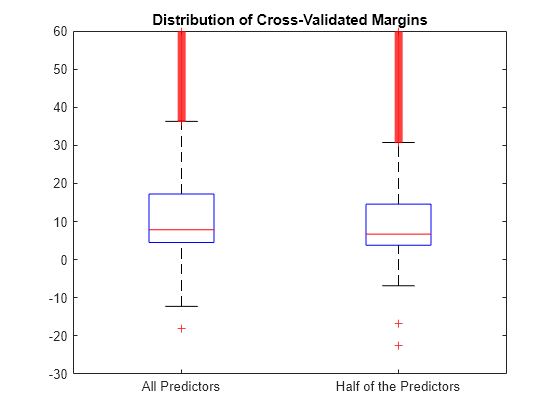
The distributions of the margins of the two classifiers are similar.

Find Good Lasso Penalty Using k-fold Margins

To determine a good lasso-penalty strength for a linear classification model that uses a logistic regression learner, compare distributions of k-fold margins.

Load the NLP data set. Preprocess the data as in Estimate k-Fold Cross-Validation Margins.

load nlpdata
Ystats = Y == 'stats';
X = X';

Create a set of 11 logarithmically-spaced regularization strengths from $$10^{-8}$$ through $$10^1$$.

Lambda = logspace(-8,1,11);

Cross-validate a binary, linear classification model using 5-fold cross-validation and that uses each of the regularization strengths. Optimize the objective function using SpaRSA. Lower the tolerance on the gradient of the objective function to 1e-8.

rng(10); % For reproducibility
CVMdl = fitclinear(X,Ystats,'ObservationsIn','columns','KFold',5, ...
    'Learner','logistic','Solver','sparsa','Regularization','lasso', ...
    'Lambda',Lambda,'GradientTolerance',1e-8)

CVMdl = 
  ClassificationPartitionedLinear
    CrossValidatedModel: 'Linear'
           ResponseName: 'Y'
        NumObservations: 31572
                  KFold: 5
              Partition: [1x1 cvpartition]
             ClassNames: [0 1]
         ScoreTransform: 'none'

CVMdl is a ClassificationPartitionedLinear model. Because fitclinear implements 5-fold cross-validation, CVMdl contains 5 ClassificationLinear models that the software trains on each fold.

Estimate the k-fold margins for each regularization strength.

m = kfoldMargin(CVMdl);
size(m)

ans = 1×2

       31572          11

m is a 31572-by-11 matrix of cross-validated margins for each observation. The columns correspond to the regularization strengths.

Plot the k-fold margins for each regularization strength. Because logistic regression scores are in [0,1], margins are in [-1,1]. Rescale the margins to help identify the regularization strength that maximizes the margins over the grid.

figure
boxplot(10000.^m)
ylabel('Exponentiated test-sample margins')
xlabel('Lambda indices')

Several values of Lambda yield k-fold margin distributions that are compacted near 10000. Higher values of lambda lead to predictor variable sparsity, which is a good quality of a classifier.

Choose the regularization strength that occurs just before the centers of the k-fold margin distributions start decreasing.

LambdaFinal = Lambda(5);

Train a linear classification model using the entire data set and specify the desired regularization strength.

MdlFinal = fitclinear(X,Ystats,'ObservationsIn','columns', ...
    'Learner','logistic','Solver','sparsa','Regularization','lasso', ...
    'Lambda',LambdaFinal);

To estimate labels for new observations, pass MdlFinal and the new data to predict.

Input Arguments

CVMdl — Cross-validated, binary, linear classification model

ClassificationPartitionedLinear model object

Cross-validated, binary, linear classification model, specified as a ClassificationPartitionedLinear model object. You can create a ClassificationPartitionedLinear model using fitclinear and specifying any one of the cross-validation, name-value pair arguments, for example, CrossVal.

To obtain estimates, kfoldMargin applies the same data used to cross-validate the linear classification model (X and Y).

Output Arguments

m — Cross-validated classification margins

numeric vector | numeric matrix

Cross-validated classification margins, returned as a numeric vector or matrix.

m is n-by-L, where n is the number of observations in the data that created CVMdl (see X and Y) and L is the number of regularization strengths in CVMdl (that is, numel(CVMdl.Trained{1}.Lambda)).

m(i,j) is the cross-validated classification margin of observation i using the linear classification model that has regularization strength CVMdl.Trained{1}.Lambda(j).

Data Types: single | double

More About

Classification Margin

The classification margin for binary classification is, for each observation, the difference between the classification score for the true class and the classification score for the false class.

The software defines the classification margin for binary classification as

$$m=2yf\left(x\right).$$

x is an observation. If the true label of x is the positive class, then y is 1, and –1 otherwise. f(x) is the positive-class classification score for the observation x. The classification margin is commonly defined as m = yf(x).

If the margins are on the same scale, then they serve as a classification confidence measure. Among multiple classifiers, those that yield greater margins are better.

Classification Score

For linear classification models, the raw classification score for classifying the observation x, a row vector, into the positive class is defined by

$$f_j(x)=x{\beta }_j+b_j.$$

For the model with regularization strength j, $${\beta }_j$$ is the estimated column vector of coefficients (the model property Beta(:,j)) and $$b_j$$ is the estimated, scalar bias (the model property Bias(j)).

The raw classification score for classifying x into the negative class is –f(x). The software classifies observations into the class that yields the positive score.

If the linear classification model consists of logistic regression learners, then the software applies the 'logit' score transformation to the raw classification scores (see ScoreTransform).

Extended Capabilities

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced in R2016a

R2024a: Specify GPU arrays (requires Parallel Computing Toolbox)

kfoldMargin fully supports GPU arrays.

R2023b: Observations with missing predictor values are used in resubstitution and cross-validation computations

Starting in R2023b, the following classification model object functions use observations with missing predictor values as part of resubstitution ("resub") and cross-validation ("kfold") computations for classification edges, losses, margins, and predictions.

Model Type	Model Objects	Object Functions
Discriminant analysis classification model	ClassificationDiscriminant	resubEdge, resubLoss, resubMargin, resubPredict
	ClassificationPartitionedModel	kfoldEdge, kfoldLoss, kfoldMargin, kfoldPredict
Ensemble of discriminant analysis learners for classification	ClassificationEnsemble	resubEdge, resubLoss, resubMargin, resubPredict
	ClassificationPartitionedEnsemble	kfoldEdge, kfoldLoss, kfoldMargin, kfoldPredict
Gaussian kernel classification model	ClassificationPartitionedKernel	kfoldEdge, kfoldLoss, kfoldMargin, kfoldPredict
	ClassificationPartitionedKernelECOC	kfoldEdge, kfoldLoss, kfoldMargin, kfoldPredict
Linear classification model	ClassificationPartitionedLinear	kfoldEdge, kfoldLoss, kfoldMargin, kfoldPredict
	ClassificationPartitionedLinearECOC	kfoldEdge, kfoldLoss, kfoldMargin, kfoldPredict
Neural network classification model	ClassificationNeuralNetwork	resubEdge, resubLoss, resubMargin, resubPredict
	ClassificationPartitionedModel	kfoldEdge, kfoldLoss, kfoldMargin, kfoldPredict
Support vector machine (SVM) classification model	ClassificationSVM	resubEdge, resubLoss, resubMargin, resubPredict
	ClassificationPartitionedModel	kfoldEdge, kfoldLoss, kfoldMargin, kfoldPredict

In previous releases, the software omitted observations with missing predictor values from the resubstitution and cross-validation computations.