knnsearch
Find k-nearest neighbors using input data
Description
Idx = knnsearch(X,Y,Name,Value)Idx with additional options specified using one or more
name-value pair arguments. For example, you can specify the number of nearest
neighbors to search for and the distance metric used in the search.
Examples
Find the patients in the hospital data set that most closely resemble the patients in Y, according to age and weight.
Load the hospital data set.
load hospital; X = [hospital.Age hospital.Weight]; Y = [20 162; 30 169; 40 168; 50 170; 60 171]; % New patients
Perform a knnsearch between X and Y to find indices of nearest neighbors.
Idx = knnsearch(X,Y);
Find the patients in X closest in age and weight to those in Y.
X(Idx,:)
ans = 5×2
25 171
25 171
39 164
49 170
50 172
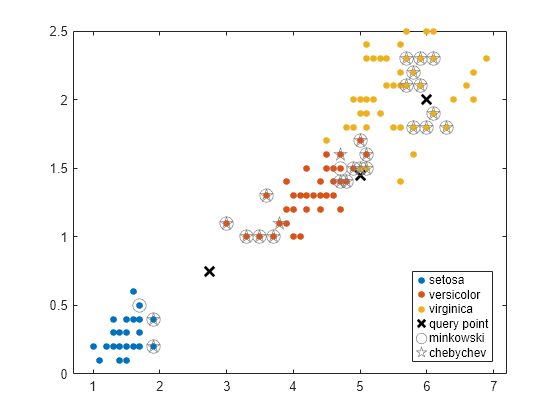
Find the 10 nearest neighbors in X to each point in Y, first using the Minkowski distance metric and then using the Chebychev distance metric.
Load Fisher's iris data set.
load fisheriris X = meas(:,3:4); % Measurements of original flowers Y = [5 1.45;6 2;2.75 .75]; % New flower data
Perform a knnsearch between X and the query points Y using Minkowski and Chebychev distance metrics.
[mIdx,mD] = knnsearch(X,Y,'K',10,'Distance','minkowski','P',5); [cIdx,cD] = knnsearch(X,Y,'K',10,'Distance','chebychev');
Visualize the results of the two nearest neighbor searches. Plot the training data. Plot the query points with the marker X. Use circles to denote the Minkowski nearest neighbors. Use pentagrams to denote the Chebychev nearest neighbors.
gscatter(X(:,1),X(:,2),species) line(Y(:,1),Y(:,2),'Marker','x','Color','k',... 'Markersize',10,'Linewidth',2,'Linestyle','none') line(X(mIdx,1),X(mIdx,2),'Color',[.5 .5 .5],'Marker','o',... 'Linestyle','none','Markersize',10) line(X(cIdx,1),X(cIdx,2),'Color',[.5 .5 .5],'Marker','p',... 'Linestyle','none','Markersize',10) legend('setosa','versicolor','virginica','query point',... 'minkowski','chebychev','Location','best')
Create two large matrices of points, and then measure the time used by knnsearch with the default "euclidean" distance metric.
rng default % For reproducibility N = 10000; X = randn(N,1000); Y = randn(N,1000); Idx = knnsearch(X,Y); % Warm up function for more reliable timing information tic Idx = knnsearch(X,Y); standard = toc
standard = 8.5191
Next, measure the time used by knnsearch with the "fasteuclidean" distance metric. Specify a cache size of 100.
Idx2 = knnsearch(X,Y,Distance="fasteuclidean",CacheSize=100); % Warm up function tic Idx2 = knnsearch(X,Y,Distance="fasteuclidean",CacheSize=100); accelerated = toc
accelerated = 1.1183
Evaluate how many times faster the accelerated computation is compared to the standard.
standard/accelerated
ans = 7.6180
The accelerated version is more than three times faster for this example.
Input Arguments
Input data, specified as a numeric matrix. Rows of X
correspond to observations, and columns correspond to variables.
Data Types: single | double
Query points, specified as a numeric matrix. Rows of
Y correspond to observations, and columns
correspond to variables. Y must have the same number of
columns as X.
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: knnsearch(X,Y,'K',10,'IncludeTies',true,'Distance','cityblock')
searches for 10 nearest neighbors, including ties and using the city block
distance.
Flag to include all nearest neighbors that have the same distance from
query points, specified as the comma-separated pair consisting of
'IncludeTies' and false
(0) or true
(1).
If 'IncludeTies' is false, then
knnsearch chooses the observation with the
smallest index among the observations that have the same distance from a
query point.
If 'IncludeTies' is true, then:
knnsearchincludes all nearest neighbors whose distances are equal to the kth smallest distance in the output arguments. To specify k, use the'K'name-value pair argument.IdxandDare m-by-1cell arrays such that each cell contains a vector of at least k indices and distances, respectively. Each vector inDcontains distances arranged in ascending order. Each row inIdxcontains the indices of the nearest neighbors corresponding to the distances inD.
Example: 'IncludeTies',true
Nearest neighbor search method, specified as the comma-separated pair
consisting of 'NSMethod' and one of these values.
'kdtree'— Creates and uses a Kd-tree to find nearest neighbors.'kdtree'is the default value when the number of columns inXis less than or equal to 10,Xis not sparse, and the distance metric is'euclidean','cityblock','chebychev', or'minkowski'. Otherwise, the default value is'exhaustive'.The value
'kdtree'is valid only when the distance metric is one of the four metrics noted above.'exhaustive'— Uses the exhaustive search algorithm by computing the distance values from all the points inXto each point inY.
Example: 'NSMethod','exhaustive'
Distance metric knnsearch uses, specified as one
of the values in this table or a function handle.
| Value | Description |
|---|---|
'euclidean' | Euclidean distance |
'seuclidean' | Standardized Euclidean distance. Each coordinate
difference between the rows in
X and the query matrix
Y is scaled by dividing by
the corresponding element of the standard deviation
computed from X. To specify a
different scaling, use the
'Scale' name-value
argument. |
'fasteuclidean' | Euclidean distance computed by using an
alternative algorithm that saves time when the
number of predictors is at least 10. In some cases,
this faster algorithm can reduce accuracy. This
distance metric is available only when
NSMethod is
'exhaustive'. Algorithms
starting with 'fast' do not
support sparse data. For details, see Algorithms. |
'fastseuclidean' | Standardized Euclidean distance computed by using
an alternative algorithm that saves time when the
number of predictors is at least 10. In some cases,
this faster algorithm can reduce accuracy. This
distance metric is available only when
NSMethod is
'exhaustive'. Algorithms
starting with 'fast' do not
support sparse data. For details, see Algorithms. |
'cityblock' | City block distance |
'chebychev' | Chebychev distance (maximum coordinate difference) |
'minkowski' | Minkowski distance. The default exponent is 2. To
specify a different exponent, use the
'P' name-value
argument. |
'mahalanobis' | Mahalanobis distance, computed using a positive
definite covariance matrix. To change the value of
the covariance matrix, use the
'Cov' name-value
argument. |
'cosine' | One minus the cosine of the included angle between observations (treated as vectors) |
'correlation' | One minus the sample linear correlation between observations (treated as sequences of values) |
'spearman' | One minus the sample Spearman's rank correlation between observations (treated as sequences of values) |
'hamming' | Hamming distance, which is the percentage of coordinates that differ |
'jaccard' | One minus the Jaccard coefficient, which is the percentage of nonzero coordinates that differ |
You can also specify a function handle for a custom
distance metric by using @ (for example,
@distfun). A custom distance function must:
Have the form
function D2 = distfun(ZI,ZJ).Take as arguments:
A 1-by-n vector
ZIcontaining a single row fromXor from the query pointsY.An m2-by-n matrix
ZJcontaining multiple rows ofXorY.
Return an m2-by-1 vector of distances
D2, whosejth element is the distance between the observationsZIandZJ(j,:).
For more information, see Distance Metrics.
Example: 'Distance','chebychev'
Data Types: char | string | function_handle
Size of the Gram matrix in megabytes, specified as a positive scalar
or "maximal". The knnsearch
function can use CacheSize only when the
Distance name-value argument begins with
fast and the NSMethod
name-value argument is set to 'exhaustive'.
If you set CacheSize to
"maximal", knnsearch tries
to allocate enough memory for an entire intermediate matrix whose size
is MX-by-MY, where
MX is the number of rows of the input data
X, and MY is the number of
rows of the input data Y. The cache size does not
have to be large enough for an entire intermediate matrix, but must be
at least large enough to hold an MX-by-1 vector.
Otherwise, knnsearch uses the standard algorithm
for computing Euclidean distance.
If the value of the Distance argument begins with
fast, the value of NSMethod
is 'exhaustive', and the value of
CacheSize is too large or
"maximal", knnsearch might
try to allocate a Gram matrix that exceeds the available memory. In this
case, MATLAB® issues an error.
Example: CacheSize="maximal"
Data Types: double | char | string
Exponent for the Minkowski distance metric, specified as the comma-separated pair consisting of 'P' and a positive scalar.
This argument is valid only if 'Distance' is 'minkowski'.
Example: 'P',3
Data Types: single | double
Covariance matrix for the Mahalanobis distance metric, specified as the comma-separated pair
consisting of 'Cov' and a positive definite matrix.
This argument is valid only if 'Distance' is 'mahalanobis'.
Example: 'Cov',eye(4)
Data Types: single | double
Scale parameter value for the standardized Euclidean distance metric,
specified as the comma-separated pair consisting of
'Scale' and a nonnegative numeric vector.
'Scale' has length equal to the number of columns
in X. When knnsearch computes
the standardized Euclidean distance, each coordinate of
X is scaled by the corresponding element of
'Scale', as is each query point. This argument is
valid only when 'Distance' is
'seuclidean'.
Example: 'Scale',quantile(X,0.75) -
quantile(X,0.25)
Data Types: single | double
Maximum number of data points in the leaf node of the
Kd-tree, specified as the comma-separated pair
consisting of 'BucketSize' and a positive integer.
This argument is valid only when NSMethod is
'kdtree'.
Example: 'BucketSize',20
Data Types: single | double
Flag to sort returned indices according to distance, specified as the
comma-separated pair consisting of 'SortIndices' and
either true (1) or
false (0).
For faster performance, you can set SortIndices
to false when the following are true:
Ycontains many observations that have many nearest neighbors inX.NSMethodis'kdtree'.IncludeTiesisfalse.
In this case, knnsearch returns the
indices of the nearest neighbors in no particular order. When
SortIndices is true, the
function arranges the nearest neighbor indices in ascending order by
distance.
SortIndices is true by
default. When NSMethod is
'exhaustive' or IncludeTies
is true, the function always sorts the
indices.
Example: 'SortIndices',false
Data Types: logical
Output Arguments
Input data indices of the nearest neighbors, returned as a numeric matrix or cell array of numeric vectors.
If you do not specify
IncludeTies(falseby default), thenIdxis an m-by-k numeric matrix, where m is the number of rows inYand k is the number of searched nearest neighbors.Idx(j,i)indicates thatX(Idx(j,i),:)is one of the k closest observations inXto the query pointY(j,:).If you specify
'IncludeTies',true, thenIdxis an m-by-1cell array such that cellj(Idx{j}) contains a vector of at least k indices of the closest observations inXto the query pointY(j,:).
If SortIndices is true, then
knnsearch arranges the indices in ascending order
by distance.
Distances of the nearest neighbors to the query points, returned as a numeric matrix or cell array of numeric vectors.
If you do not specify
IncludeTies(falseby default), thenDis an m-by-k numeric matrix, where m is the number of rows inYand k is the number of searched nearest neighbors.D(j,i)is the distance betweenX(Idx(j,i),:)andY(j,:)with respect to the distance metric.If you specify
'IncludeTies',true, thenDis an m-by-1cell array such that cellj(D{j}) contains a vector of at least k distances of the closest observations inXto the query pointY(j,:).
If SortIndices is true, then
knnsearch arranges the distances in ascending
order.
Tips
For a fixed positive integer k,
knnsearchfinds the k points inXthat are the nearest to each point inY. To find all points inXwithin a fixed distance of each point inY, userangesearch.knnsearchdoes not save a search object. To create a search object, usecreatens.
Algorithms
For information on a specific search algorithm, see k-Nearest Neighbor Search and Radius Search.
The values of the Distance argument that begin fast
(such as "fasteuclidean" and "fastseuclidean")
calculate Euclidean distances using an algorithm that uses extra memory to save
computational time. This algorithm is named "Euclidean Distance Matrix Trick" in Albanie
[1] and elsewhere. Internal
testing shows that this algorithm saves time when the number of predictors is at least 10.
Algorithms starting with fast do not support sparse data.
To find the matrix D of distances between all the points xi and xj, where each xi has n variables, the algorithm computes distance using the final line in the following equations:
The matrix in the last line of the equations is called the Gram matrix. Computing the set of squared distances is faster, but slightly less numerically stable, when you compute and use the Gram matrix instead of computing the squared distances by squaring and summing. For more details, see Albanie [1].
To store the Gram matrix, the software uses a cache with the default size of
1e3 megabytes. You can set the cache size using the
CacheSize name-value argument. If the value of
CacheSize is too large or "maximal", then the
software might try to allocate a Gram matrix that exceeds the available memory. In this
case, the software issues an error.
References
[1] Albanie, Samuel. Euclidean Distance Matrix Trick. June, 2019. Available at https://samuelalbanie.com/files/Euclidean_distance_trick.pdf.
Alternative Functionality
If you set the knnsearch function's 'NSMethod'
name-value pair argument to the appropriate value ('exhaustive' for
an exhaustive search algorithm or 'kdtree' for a
Kd-tree algorithm), then the search results are equivalent to the
results obtained by conducting a distance search using the knnsearch object function. Unlike the knnsearch
function, the knnsearch object function requires an
ExhaustiveSearcher or a KDTreeSearcher model object.
Simulink Block
To integrate a k-nearest neighbor search into Simulink®, you can use the KNN Search
block in the Statistics and Machine Learning Toolbox™ library or a MATLAB Function block with the knnsearch function. For
an example, see Predict Class Labels Using MATLAB Function Block.
When deciding which approach to use, consider the following:
If you use the Statistics and Machine Learning Toolbox library block, you can use the Fixed-Point Tool (Fixed-Point Designer) to convert a floating-point model to fixed point.
Support for variable-size arrays must be enabled for a MATLAB Function block with the
knnsearchfunction.
References
[1] Friedman, J. H., J. Bentley, and R. A. Finkel. “An Algorithm for Finding Best Matches in Logarithmic Expected Time.” ACM Transactions on Mathematical Software 3, no. 3 (1977): 209–226.
Extended Capabilities
The
knnsearch function supports tall arrays with the following usage
notes and limitations:
If
Xis a tall array, thenYcannot be a tall array. Similarly, ifYis a tall array, thenXcannot be a tall array.
For more information, see Tall Arrays.
Usage notes and limitations:
For code generation, the default value of the
'NSMethod'name-value pair argument is'exhaustive'when the number of columns inXis greater than 7.The value of the
'Distance'name-value pair argument must be a compile-time constant and cannot be a custom distance function.The value of the
'IncludeTies'name-value pair argument must be a compile-time constant.The
'SortIndices'name-value pair argument is not supported. The output arguments are always sorted.knnsearchdoes not support code generation for fast Euclidean distance computations, meaning those distance metrics whose names begin withfast(for example,'fasteuclidean').Names in name-value arguments must be compile-time constants. For example, to allow a user-defined exponent for the Minkowski distance in the generated code, include
{coder.Constant('Distance'),coder.Constant('Minkowski'),coder.Constant('P'),0}in the-argsvalue ofcodegen(MATLAB Coder).When you specify
'IncludeTies'astrue, the sorted order of tied distances in the generated code can be different from the order in MATLAB due to numerical precision.When
knnsearchuses the kd-tree search algorithm, and the code generation build type is a MEX function,codegen(MATLAB Coder) generates a MEX function using Intel® Threading Building Blocks (TBB) for parallel computation. Otherwise,codegengenerates code usingparfor(MATLAB Coder).MEX function for the kd-tree search algorithm —
codegengenerates an optimized MEX function using Intel TBB for parallel computation on multicore platforms. You can use the MEX function to accelerate MATLAB algorithms. For details on Intel TBB, see https://www.intel.com/content/www/us/en/developer/tools/oneapi/onetbb.html.If you generate the MEX function to test the generated code of the
parforversion, you can disable the usage of Intel TBB. Set theExtrinsicCallsproperty of the MEX configuration object tofalse. For details, seecoder.MexCodeConfig(MATLAB Coder).MEX function for the exhaustive search algorithm and standalone C/C++ code for both algorithms — The generated code of
knnsearchusesparfor(MATLAB Coder) to create loops that run in parallel on supported shared-memory multicore platforms in the generated code. If your compiler does not support the Open Multiprocessing (OpenMP) application interface or you disable OpenMP library, MATLAB Coder™ treats theparfor-loops asfor-loops. To find supported compilers, see Supported Compilers. To disable OpenMP library, set theEnableOpenMPproperty of the configuration object tofalse. For details, seecoder.CodeConfig(MATLAB Coder).
knnsearchreturns integer-type (int32) indices in generated standalone C/C++ code. Therefore, the function allows for strict single-precision support when you use single-precision inputs. For MEX code generation, the function still returns double-precision indices to match the MATLAB behavior.
For more information on code generation, see Introduction to Code Generation and General Code Generation Workflow.
Usage notes and limitations:
The
NSMethodname-value argument must be specified as"exhaustive".The
IncludeTiesandSortIndicesname-value arguments must be specified as their default values.You cannot specify the
Distancename-value argument as"fasteuclidean"or"fastseuclidean".
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2010aThe 'fasteuclidean' and 'fastseuclidean'
distance metrics accelerate the computation of Euclidean distances by using a cache
and a different algorithm (see Algorithms). Set the size
of the cache using the CacheSize name-value argument.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)