plotAdded
Added variable plot of linear regression model
Syntax
Description
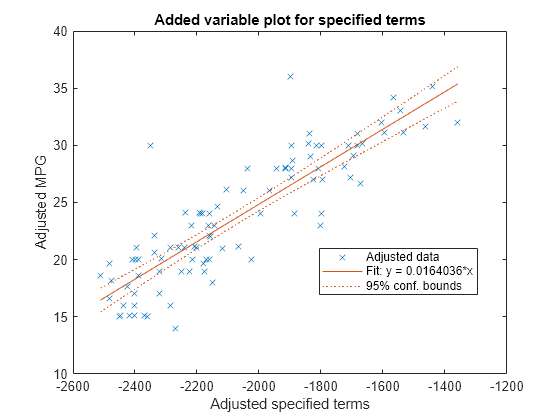
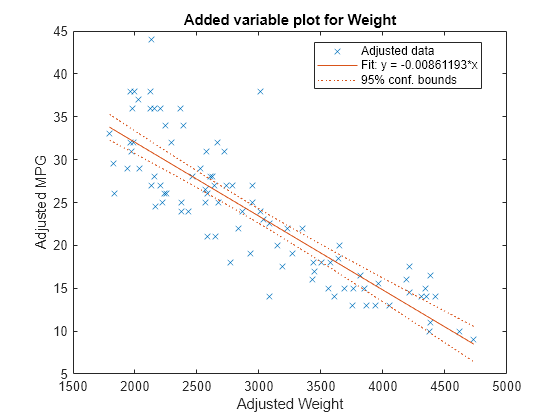
plotAdded( creates an added variable plot for the whole model
mdl)mdl except the constant (intercept) term.
plotAdded(
specifies graphical properties of adjusted data points using one or more
name-value pair arguments. For example, you can specify the marker symbol and
size for the data points.mdl,coef,Name,Value)
plotAdded(
creates the plot in the axes specified by ax,___)ax instead of the
current axes, using any of the input argument combinations in the previous
syntaxes.
h = plotAdded(___)h to modify the
properties of a specific line after you create the plot. For a list of
properties, see Line Properties.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Tips
The data cursor displays the values of the selected plot point in a data tip (small text box located next to the data point). The data tip includes the x-axis and y-axis values for the selected point, along with the observation name or number.
Alternative Functionality
A
LinearModelobject provides multiple plotting functions.When creating a model, use
plotAddedto understand the effect of adding or removing a predictor variable.When verifying a model, use
plotDiagnosticsto find questionable data and to understand the effect of each observation. Also, useplotResidualsto analyze the residuals of the model.After fitting a model, use
plotAdjustedResponse,plotPartialDependence, andplotEffectsto understand the effect of a particular predictor. UseplotInteractionto understand the interaction effect between two predictors. Also, useplotSliceto plot slices through the prediction surface.
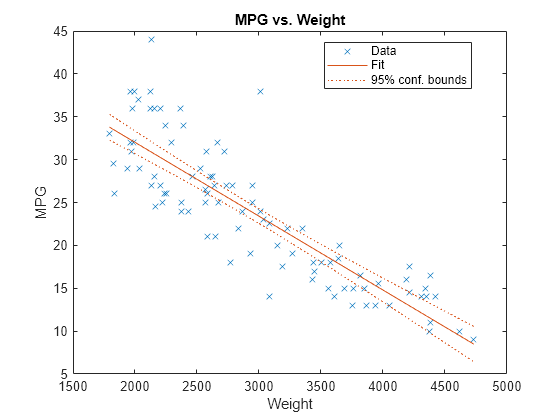
plotAddedshows the incremental effect on the response of specified terms by removing the effects of the other terms, whereasplotAdjustedResponseshows the effect of a selected predictor in the model fit with the other predictors averaged out by averaging the fitted values. Note that the definitions of adjusted values inplotAddedandplotAdjustedResponseare not the same.
Extended Capabilities
Version History
Introduced in R2012a