comm.AWGNChannel

Add white Gaussian noise to input signal

Description

comm.AWGNChannel adds white Gaussian noise to the input signal.

When applicable, if inputs to the object have a variable number of channels, the EbNo, EsNo, SNR, BitsPerSymbol, SignalPower, SamplesPerSymbol, and Variance properties must be scalars.

To add white Gaussian noise to an input signal:

1. Create the comm.AWGNChannel object and set its properties.

2. Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

Creation

Syntax

awgnchan = comm.AWGNChannel

awgnchan = comm.AWGNChannel(Name,Value)

Description

awgnchan = comm.AWGNChannel creates an additive white Gaussian noise (AWGN) channel System object™, awgnchan. This object then adds white Gaussian noise to a real or complex input signal.

awgnchan = comm.AWGNChannel(Name,Value) creates a AWGN channel object, awgnchan, with the specified property Name set to the specified Value. You can specify additional name-value pair arguments in any order as (Name1,Value1,...,NameN,ValueN).

Properties

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and the release function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, see System Design in MATLAB Using System Objects.

NoiseMethod — Noise level method

'Signal to noise ratio (Eb/No)' (default) | 'Signal to noise ratio (Es/No)' | 'Signal to noise ratio (SNR)' | 'Variance'

Noise level method, specified as 'Signal to noise ratio (Eb/No)', 'Signal to noise ratio (Es/No)', 'Signal to noise ratio (SNR)', or 'Variance'. For more information, see Relationship Between Eb/No, Es/No, and SNR Modes and Specifying Variance Directly or Indirectly.

Data Types: char

EbNo — Ratio of energy per bit to noise power spectral density

10 (default) | scalar | row vector

Ratio of energy per bit to noise power spectral density (Eb/No) in decibels, specified as a scalar or 1-by-N_C vector. N_C is the number of channels.

Tunable: Yes

Dependencies

This property applies when NoiseMethod is set to 'Signal to noise ratio (Eb/No)'.

Data Types: double

EsNo — Ratio of energy per symbol to noise power spectral density

10 (default) | scalar | row vector

Ratio of energy per symbol to noise power spectral density (Es/No) in decibels, specified as a scalar or 1-by-N_C vector. N_C is the number of channels.

Tunable: Yes

Dependencies

This property applies when NoiseMethod is set to 'Signal to noise ratio (Es/No)'.

Data Types: double

SNR — Ratio of signal power to noise power

10 (default) | scalar | row vector

Ratio of signal power to noise power in decibels, specified as a scalar or 1-by-N_C vector. N_C is the number of channels.

Tunable: Yes

Dependencies

This property applies when NoiseMethod is set to 'Signal to noise ratio (SNR)'.

Data Types: double

BitsPerSymbol — Number of bits per symbol

1 (default) | positive integer

Number of bits per symbol, specified as a positive integer.

Dependencies

This property applies when NoiseMethod is set to 'Signal to noise ratio (Eb/No)'.

Data Types: double

SignalPower — Input signal power

1 (default) | positive scalar | row vector

Input signal power in watts, specified as a positive scalar or 1-by-N_C vector. N_C is the number of channels. The object assumes a nominal impedance of 1 Ω.

Tunable: Yes

Dependencies

This property applies when NoiseMethod is set to 'Signal to noise ratio (Eb/No)', 'Signal to noise ratio (Es/No)', or 'Signal to noise ratio (SNR)'.

Data Types: double

SamplesPerSymbol — Number of samples per symbol

1 (default) | positive integer | row vector

Number of samples per symbol, specified as a positive integer or 1-by-N_C vector. N_C is the number of channels.

Dependencies

This property applies when NoiseMethod is set to 'Signal to noise ratio (Eb/No)' or 'Signal to noise ratio (Es/No)'.

Data Types: double

VarianceSource — Source of noise variance

'Property' (default) | 'Input port'

Source of noise variance, specified as 'Property' or 'Input port'.

• Set VarianceSource to 'Property' to specify the noise variance value using the Variance property.

• Set VarianceSource to 'Input port' to specify the noise variance value using an input to the object, when you call it as a function.

For more information, see Specifying Variance Directly or Indirectly.

Dependencies

This property applies when NoiseMethod is 'Variance'.

Data Types: char

Variance — White Gaussian noise variance

1 (default) | positive scalar | row vector

White Gaussian noise variance, specified as a positive scalar or 1-by-N_C vector. N_C is the number of channels.

Tunable: Yes

Dependencies

This property applies when NoiseMethod is set to 'Variance' and VarianceSource is set to 'Property'.

Data Types: double

RandomStream — Source of random number stream

'Global stream' (default) | 'mt19937ar with seed'

Source of random number stream, specified as 'Global stream' or 'mt19937ar with seed'.

• When you set RandomStream to 'Global stream', the object uses the MATLAB^® default random stream to generate random numbers. To generate reproducible numbers using this object, you can reset the MATLAB default random stream. For example reset(RandStream.getGlobalStream). For more information, see RandStream.

• When you set RandomStream to 'mt19937ar with seed', the object uses the mt19937ar algorithm for normally distributed random number generation. In this scenario, when you call the reset function, the object reinitializes the random number stream to the value of the Seed property. You can generate reproducible numbers by resetting the object.

For a complex input signal, the object creates the random data as follows:

noise = randn(NS,NC)+1i(randn(NS,NC))

N_S is the number of samples and N_C is the number of channels.

Dependencies

This property applies when NoiseMethod is set to 'Variance'.

Data Types: char

Seed — Initial seed

67 (default) | nonnegative integer

Initial seed of the mt19937ar random number stream, specified as a nonnegative integer. For each call to the reset function, the object reinitializes the mt19937ar random number stream to the Seed value.

Dependencies

This property applies when RandomStream is set to 'mt19937ar with seed'.

Data Types: double

Usage

Syntax

outsignal = awgnchan(insignal)

outsignal = awgnchan(insignal,var)

Description

outsignal = awgnchan(insignal) adds white Gaussian noise, as specified by awgnchan, to the input signal. The result is returned in outsignal.

outsignal = awgnchan(insignal,var) specifies the variance of the white Gaussian noise. This syntax applies when you set the NoiseMethod to 'Variance' and VarianceSource to 'Input port'.

For example:

awgnchan = comm.AWGNChannel('NoiseMethod','Variance', ...
     'VarianceSource','Input port');
var = 12;
...
outsignal = awgnchan(insignal,var);

Input Arguments

insignal — Input signal

scalar | vector | matrix

Input signal, specified as a scalar, an N_S-element vector, or an N_S-by-N_C matrix. N_S is the number of samples and N_C is the number of channels.

This object accepts variable-size inputs. After the object is locked, you can change the size of each input channel, but you cannot change the number of channels. For more information, see Variable-Size Signal Support with System Objects.

Data Types: double
Complex Number Support: Yes

var — Variance of additive white Gaussian noise

positive scalar | row vector

Variance of additive white Gaussian noise, specified as a positive scalar or 1-by-N_C vector. N_C is the number of channels, as determined by the number of columns in the input signal matrix.

Output Arguments

outsignal — Output signal

matrix

Output signal, returned with the same dimensions as insignal.

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

release(obj)

Common to All System Objects

step	Run System object algorithm
release	Release resources and allow changes to System object property values and input characteristics
reset	Reset internal states of System object

Examples

Create Default AWGN Channel System Object

Create an AWGN channel System object with the default configuration. Pass signal data through this channel.

Create an AWGN channel object and signal data.

awgnchan = comm.AWGNChannel;
insignal = randi([0 1],100,1);

Send the input signal through the channel.

outsignal = awgnchan(insignal);

Add White Gaussian Noise to 8-PSK Signal

Modulate an 8-PSK signal, add white Gaussian noise, and plot the signal to visualize the effects of the noise.

Modulate the signal.

modData = pskmod(randi([0 7],2000,1),8);

Add white Gaussian noise to the modulated signal by passing the signal through an additive white Gaussian noise (AWGN) channel.

channel = comm.AWGNChannel('EbNo',20,'BitsPerSymbol',3);

Transmit the signal through the AWGN channel.

channelOutput = channel(modData);

Plot the noiseless and noisy data by using scatter plots to visualize the effects of the noise.

scatterplot(modData)

scatterplot(channelOutput)

Change the EbNo property to 10 dB to increase the noise.

channel.EbNo = 10;

Pass the modulated data through the AWGN channel.

channelOutput = channel(modData);

Plot the channel output. You can see the effects of increased noise.

scatterplot(channelOutput)

Configure AWGN Channel System Object for Coded Eb/No

To accurately represent the noise level the bit energy to noise density ratio (Eb/No) for communication links must account for the bits per symbol and coding rate of the signal transmitted through the channel.

Define the codeword and message length for a Reed-Solomon code and the modulation order of the signal.

N = 15;         % R-S codeword length in symbols
K = 9;          % R-S message length in symbols
codeRate = K/N; % R-S code rate
M = 16;         % Modulation order
bps = log2(M);  % Bits per symbol

Specify the uncoded Eb/No in dB. Convert the uncoded Eb/No to the corresponding coded Eb/No using the code rate.

UncodedEbNo = 6;
CodedEbNo = UncodedEbNo + 10*log10(codeRate);

Construct an AWGN channel object setting the number of bits per symbol and the coded Eb/No.

channel1 = comm.AWGNChannel( ...
    NoiseMethod='Signal to noise ratio (Eb/No)', ...
    BitsPerSymbol=bps, ...
    EbNo=CodedEbNo)

channel1 = 
  comm.AWGNChannel with properties:

         NoiseMethod: 'Signal to noise ratio (Eb/No)'
                EbNo: 3.7815
       BitsPerSymbol: 4
         SignalPower: 1
    SamplesPerSymbol: 1
        RandomStream: 'Global stream'

For an alternative approach, you can convert the uncoded Eb/No to the corresponding SNR, and then configure an AWGN channel object setting noise method to SNR.

snr = convertSNR(UncodedEbNo,"ebno","SNR", ...
    BitsPerSymbol=bps, ...
    CodingRate=codeRate);
channel2 = comm.AWGNChannel( ...
    NoiseMethod='Signal to noise ratio (SNR)', ...
    SNR=snr)

channel2 = 
  comm.AWGNChannel with properties:

     NoiseMethod: 'Signal to noise ratio (SNR)'
             SNR: 9.8021
     SignalPower: 1
    RandomStream: 'Global stream'

Process Signals When Number of Channels Changes

Pass a single-channel and multichannel signal through an AWGN channel System object™.

Create an AWGN channel System object with the Eb/No ratio set for a single channel input. In this case, the EbNo property is a scalar.

channel = comm.AWGNChannel('EbNo',15);

Generate random data and apply QPSK modulation.

data = randi([0 3],1000,1);
modData = pskmod(data,4,pi/4);

Pass the modulated data through the AWGN channel.

rxSig = channel(modData);

Plot the noisy constellation.

scatterplot(rxSig)

Generate two-channel input data and apply QPSK modulation.

data = randi([0 3],2000,2);
modData = pskmod(data,4,pi/4);

Pass the modulated data through the AWGN channel.

rxSig = channel(modData);

Plot the noisy constellations. Each channel is represented as a single column in rxSig. The plots are nearly identical, because the same Eb/No value is applied to both channels.

scatterplot(rxSig(:,1))
title('First Channel')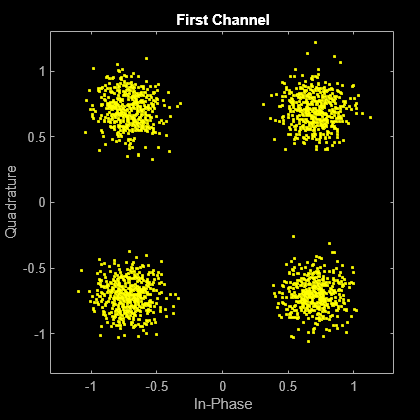

scatterplot(rxSig(:,2))
title('Second Channel')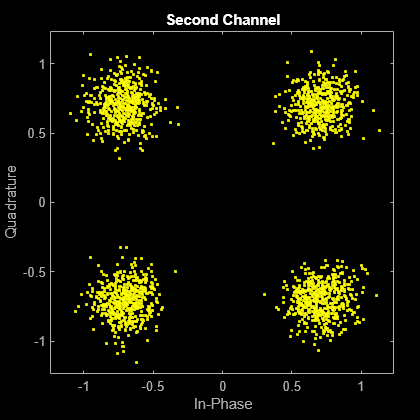

Modify the AWGN channel object to apply a different Eb/No value to each channel. To apply different values, set the EbNo property to a 1-by-2 vector. When changing the dimension of the EbNo property, you must release the AWGN channel object.

release(channel)
channel.EbNo = [10 20];

Pass the data through the AWGN channel.

rxSig = channel(modData);

Plot the noisy constellations. The first channel has significantly more noise due to its lower Eb/No value.

scatterplot(rxSig(:,1))
title('First Channel')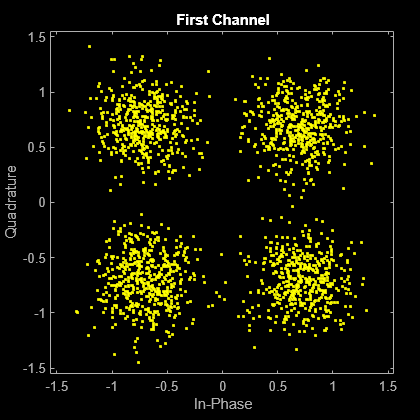

scatterplot(rxSig(:,2))
title('Second Channel')

Add AWGN Using Noise Variance Input Port

Apply the noise variance input as a scalar or a row vector, with a length equal to the number of channels of the current signal input.

Create an AWGN channel System object™ with the NoiseMethod property set to 'Variance' and the VarianceSource property set to 'Input port'.

channel = comm.AWGNChannel('NoiseMethod','Variance', ...
'VarianceSource','Input port');

Generate random data for two channels and apply 16-QAM modulation.

data = randi([0 15],10000,2);
txSig = qammod(data,16);

Pass the modulated data through the AWGN channel. The AWGN channel object processes data from two channels. The variance input is a 1-by-2 vector.

rxSig = channel(txSig,[0.01 0.1]);

Plot the constellation diagrams for the two channels. The second signal is noisier because its variance is ten times larger.

scatterplot(rxSig(:,1))

scatterplot(rxSig(:,2))

Repeat the process where the noise variance input is a scalar. The same variance is applied to both channels. The constellation diagrams are nearly identical.

rxSig = channel(txSig,0.2);
scatterplot(rxSig(:,1))

scatterplot(rxSig(:,2))

Set Random Number Seed for Repeatability

Specify a seed to produce the same outputs when using a random stream in which you specify the seed.

Create an AWGN channel System object™. Set the NoiseMethod property to 'Variance', the RandomStream property to 'mt19937ar with seed', and the Seed property to 99.

channel = comm.AWGNChannel( ...
    'NoiseMethod','Variance', ...
    'RandomStream','mt19937ar with seed', ...
    'Seed',99);

Pass data through the AWGN channel.

y1 = channel(zeros(8,1));

Pass another all-zeros vector through the channel.

y2 = channel(zeros(8,1));

Because the seed changes between function calls, the output is different.

isequal(y1,y2)

ans = logical
   0

Reset the AWGN channel object by calling the reset function. The random data stream is reset to the initial seed of 99.

reset(channel);

Pass the all-zeros vector through the AWGN channel.

y3 = channel(zeros(8,1));

Confirm that the two signals are identical.

isequal(y1,y3)

ans = logical
   1

Algorithms

Relationship Between Eb/No, Es/No, and SNR Modes

For uncoded complex input signals, comm.AWGNChannel relates E_b/N_0, E_s/N₀, and SNR according to these equations:

E_s/N₀ = N_sps × SNR

E_s/N₀ = E_b/N₀ + 10log₁₀(k) in dB

where

• E_s represents the signal energy in joules.

• E_b represents the bit energy in joules.

• N₀ represents the noise power spectral density in watts/Hz.

• N_sps represents the number of samples per symbol, SamplesPerSymbol.

• k represents the number of information bits per input symbol, BitsPerSymbol.

For real signal inputs, the comm.AWGNChannel relates E_s/N₀ and SNR according to this equation:

E_s/N₀ = 0.5 (N_sps) × SNR

Note

• All values of power assume a nominal impedance of 1 ohm.

• The equation for the real case differs from the corresponding equation for the complex case by a factor of 2. Specifically, the object uses a noise power spectral density of N₀/2 watts/Hz for real input signals, versus N₀ watts/Hz for complex signals.

For more information, see AWGN Channel Noise Level.

Specifying Variance Directly or Indirectly

To directly specify the variance of the noise generated by comm.AWGNChannel, specify VarianceSource as:

• "Property", then set NoiseMethod to "Variance" and specify the variance with the Variance property.

• "Input port", then specify the variance level for the object as an input with an input argument, var.

To specify variance indirectly, that is, to have it calculated by comm.AWGNChannel, specify VarianceSource as "Property" and the NoiseMethod as:

• "Signal to noise ratio (Eb/No)", where the object uses these properties to calculate the variance:

  • EbNo, the ratio of bit energy to noise power spectral density

  • BitsPerSymbol

  • SignalPower, the actual power of the input signal samples

  • SamplesPerSymbol

• "Signal to noise ratio (Es/No)", where the object uses these properties to calculate the variance:

  • EsNo, the ratio of signal energy to noise power spectral density

  • SignalPower, the actual power of the input signal samples

  • SamplesPerSymbol

• "Signal to noise ratio (SNR)", where the object uses these properties to calculate the variance:

  • SNR, the ratio of signal power to noise power

  • SignalPower, the actual power of the input signal samples

Changing the number of samples per symbol (SamplesPerSymbol) affects the variance of the noise added per sample, which also causes a change in the final error rate.

NoiseVariance = SignalPower × SamplesPerSymbol / 10^(EsNo/10)

Tip

Select the number of samples per symbol based on what constitutes a symbol and the oversampling applied to it. For example, a symbol could have 3 bits and be oversampled by 4. For more information, see AWGN Channel Noise Level.

References

[1] Proakis, John G. Digital Communications. 4th Ed. McGraw-Hill, 2001.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

See System Objects in MATLAB Code Generation (MATLAB Coder).

Version History

Introduced in R2012a