phased.RangeEstimator

Range estimation

expand all in page

Description

The phased.RangeEstimator System object™ estimates the ranges of targets. Input to the estimator consists of a range-response or range-Doppler response data cube, and detection locations from a detector. When information about clusters of detections is available, the ranges are computed using cluster information. Clustering associates multiple detections into one extended detection.

To compute the detections for a range-response or range-Doppler cube:

  1. Create the phased.RangeEstimator object and set its properties.

  2. Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

Creation

Syntax

estimator = phased.RangeEstimator
estimator = phased.RangeEstimator(Name=Value)

Description

estimator = phased.RangeEstimator creates a range estimator System object, estimator.

estimator = phased.RangeEstimator(Name=Value) creates a System object, estimator, with each specified property Name set to the specified Value. You can specify additional name and value arguments in any order as (Name1=Value1,...,NameN=ValueN).

Properties

expand all

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and the release function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, see System Design in MATLAB Using System Objects.

Range estimator, specified as a phased.RangeEstimator System object.

Example: phased.RangeEstimator

Source of the number of range estimates to report, specified as "Auto" or "Property".

If you set this property to "Auto", the number of reported estimates is determined from the number of columns in the detidx input to the step method. If cluster IDs are provided, the number of estimates is determined from the number of unique cluster IDs in the clusterids input to the step method.

If you set this property to "Property", the number of reported estimates is obtained from the value of the NumEstimates property.

Example: "Property"

Data Types: char

The maximum number of range estimates to report, specified as a positive integer. The number of requested estimates can be greater than the number of columns in the detidx argument or the number of unique IDs in the clusterids argument of the step method. In that case, the remainder is filled with NaN.

Dependencies

To enable this property, set the NumEstimatesSource property to "Property".

Data Types: single | double

Option to accept cluster IDs as an input argument to the step method, specified as false or true. Setting this property to true enables the clusterids input argument.

Example: false

Data Types: logical

Option to enable output of range estimate variances, specified as false or true. Range variances are returned by the rngvar output argument of the step method.

Example: false

Data Types: logical

Root-mean-square range resolution of the detection, specified as a positive scalar. The value of the RMSResolution must have the same units as the rangegrid input argument of the step method.

Dependencies

To enable this property, set the value of the VarianceOutputPort property to true.

Data Types: single | double

Source of noise power values, specified as "Property" or "Input port". Noise power is used to compute range estimation variance and SNR. If you set this property to "Property", the value of the NoisePower property represents the noise power at the detection locations. If you set this property to "Input port", you can specify noise power using the noisepower input argument, of the step method.

Example: "Input port"

Data Types: char

Constant noise power value over the range-response or range-Doppler response data cube, specified as a positive real scalar. Noise power units are linear. The same noise power value is applied to all detections.

Dependencies

To enable this property, set the value of the VarianceOutputPort property to true and set NoisePowerSource to "Property".

Data Types: single | double

Usage

Syntax

rngest = estimator(resp,rnggrid,detidx)
[rngest,rngvar] = estimator(resp,rnggrid,detidx,noisepower)
[rngest,rngvar] = estimator(resp,rnggrid,detidx,clusterids)
[rngest,rngvar] = estimator(resp,rnggrid,detidx,noisepower,clusterids)

Description

rngest = estimator(resp,rnggrid,detidx) estimates ranges from detections derived from the range response data cube, resp. Range estimates are computed for each detection position reported in detidx. The rnggrid argument sets the units for the range dimension of the response data cube.

[rngest,rngvar] = estimator(resp,rnggrid,detidx,noisepower) also specifies the noise power. This syntax applies when you set the VarianceOutputPort property to true and the NoisePowerSource property to "Input port".

example

[rngest,rngvar] = estimator(resp,rnggrid,detidx,clusterids) also specifies the cluster IDs for the detections. This syntax applies when you set the ClusterInputPort to true.

You can combine optional input and output arguments when their enabling properties are set. Optional inputs and outputs must be listed in the same order as the order of the enabling properties. For example, [rngest,rngvar] = estimator(resp,rnggrid,detidx,noisepower,clusterids).

Note

The object performs an initialization the first time the object is executed. This initialization locks nontunable properties and input specifications, such as dimensions, complexity, and data type of the input data. If you change a nontunable property or an input specification, the System object issues an error. To change nontunable properties or inputs, you must first call the release method to unlock the object.

Input Arguments

expand all

Range-processed response data cube, specified as a complex-valued M-by-1 column vector, a complex-valued M-by-N matrix, or a complex-valued M-by-N-by-P array. M is the number of fast-time or range samples. N is the number of spatial elements, such as sensor elements or beams, P is the number of Doppler bins or pulses, depending on whether the data cube has been Doppler processed.

The size of the first dimension of the input matrix can vary to simulate a changing signal length. A size change can occur, for example, in the case of a pulse waveform with variable pulse repetition frequency.

Data Types: single | double

Range values along range dimension of the resp argument, specified as a real-valued M-by-1 column vector. rnggrid defines the range values corresponding to the fast-time or range dimension. Range values must be monotonically increasing and equally spaced. Units are in meters.

Example: [0.1,0.2,0.3]

Data Types: single | double

Detection indices, specified as a real-valued Nd-by-Q matrix. Q is the number of detections and Nd is the number of dimensions of the response data cube, resp. Each column of detidx contains the Nd indices of the detection in the response data cube.

To generate detection indices, you can use the phased.CFARDetector object or phased.CFARDetector2D object.

Data Types: single | double

Noise power at detection locations, specified as a positive scalar or real-valued 1-by-Q row vector where Q is the number of detections specified in detidx.

Dependencies

To enable this input argument, set the value of the NoisePowerSource property to "Input port".

Data Types: single | double

Cluster IDs, specified as a real-valued 1-by-Q row vector, where Q is the number of detections specified in detidx. Each element of clusterids corresponds to a column in detidx. Detections with the same cluster ID are in the same cluster.

Dependencies

To enable this input argument, set the value of the ClusterInputPort property to true.

Data Types: single | double

Output Arguments

expand all

Range estimates, returned as a real-valued K-by-1 column vector.

  • When ClusterInputPort is false, range estimates are computed for each detection location in the detidx argument. Then K equals the column dimension, Q, of detidx.

  • When ClusterInputPort is true, range estimates are computed for each cluster ID in the clusterids argument. Then K equals the number of unique cluster IDs, Q.

Data Types: single | double

Range estimation variance, returned as a positive, real-valued K-by-1 column vector, where K is the dimension of rngest. Each element of rngvar corresponds to an element of rngest. The estimator variance is computed using the Ziv-Zakai bound.

Data Types: single | double

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

release(obj)

expand all

stepRun System object algorithm
releaseRelease resources and allow changes to System object property values and input characteristics
resetReset internal states of System object

Examples

collapse all

Open Live Script

To estimate the range and speed of three targets, create a range-Doppler map using the phased.RangeDopplerResponse System object™. Then use the phased.RangeEstimator and phased.DopplerEstimator System objects to estimate range and speed. The transmitter and receiver are collocated isotropic antenna elements forming a monostatic radar system.

The transmitted signal is a linear FM waveform with a pulse repetition interval (PRI) of 7.0 μs and a duty cycle of 2%. The operating frequency is 77 GHz and the sample rate is 150 MHz.

fs = 150e6;
c = physconst("LightSpeed");
fc = 77.0e9;
pri = 7e-6;
prf = 1/pri;

Set up the scenario parameters. The transmitter and receiver are stationary and located at the origin. The targets are 500, 530, and 750 meters from the radar along the x-axis. The targets move along the x-axis at speeds of –60, 20, and 40 m/s. All three targets have a nonfluctuating radar cross-section (RCS) of 10 dB. Create the target and radar platforms.

Numtgts = 3;
tgtpos = zeros(Numtgts);
tgtpos(1,:) = [500 530 750];
tgtvel = zeros(3,Numtgts);
tgtvel(1,:) = [-60 20 40];
tgtrcs = db2pow(10)*[1 1 1];
tgtmotion = phased.Platform(tgtpos,tgtvel);
target = phased.RadarTarget(PropagationSpeed=c,OperatingFrequency=fc, ...
    MeanRCS=tgtrcs);
radarpos = [0;0;0];
radarvel = [0;0;0];
radarmotion = phased.Platform(radarpos,radarvel);

Create the transmitter and receiver antennas.

txantenna = phased.IsotropicAntennaElement;
rxantenna = clone(txantenna);

Set up the transmitter-end signal processing. Create an upsweep linear FM signal with a bandwidth of one half the sample rate. Find the length of the PRI in samples and then estimate the rms bandwidth and range resolution.

bw = fs/2;
waveform = phased.LinearFMWaveform(SampleRate=fs, ...
    PRF=prf,OutputFormat="Pulses",NumPulses=1,SweepBandwidth=fs/2, ...
    DurationSpecification="Duty cycle",DutyCycle=0.02);
sig = waveform();
Nr = length(sig);
bwrms = bandwidth(waveform)/sqrt(12);
rngrms = c/bwrms;

Set up the transmitter and radiator System object properties. The peak output power is 10 W and the transmitter gain is 36 dB.

peakpower = 10;
txgain = 36.0;
transmitter = phased.Transmitter( ...
    PeakPower=peakpower, ...
    Gain=txgain, ...
    InUseOutputPort=true);
radiator = phased.Radiator( ...
    Sensor=txantenna,...
    PropagationSpeed=c,...
    OperatingFrequency=fc);

Set up the free-space channel in two-way propagation mode.

channel = phased.FreeSpace( ...
    SampleRate=fs, ...    
    PropagationSpeed=c, ...
    OperatingFrequency=fc, ...
    TwoWayPropagation=true);

Set up the receiver-end processing. Set the receiver gain and noise figure.

collector = phased.Collector( ...
    Sensor=rxantenna, ...
    PropagationSpeed=c, ...
    OperatingFrequency=fc);
rxgain = 42.0;
noisefig = 1;
receiver = phased.ReceiverPreamp( ...
    SampleRate=fs, ...
    Gain=rxgain, ...
    NoiseFigure=noisefig);

Loop over the pulses to create a data cube of 128 pulses. For each step of the loop, move the target and propagate the signal. Then put the received signal into the data cube. The data cube contains the received signal per pulse. Ordinarily, a data cube has three dimensions where the last dimension corresponds to antennas or beams. Because only one sensor is used, the cube has only two dimensions.

The processing steps are:

  1. Move the radar and targets.

  2. Transmit a waveform.

  3. Propagate the waveform signal to the target.

  4. Reflect the signal from the target.

  5. Propagate the waveform back to the radar. Two-way propagation enables you to combine the return propagation with the outbound propagation.

  6. Receive the signal at the radar.

  7. Load the signal into the data cube.

Np = 128;
dt = pri;
cube = zeros(Nr,Np);
for n = 1:Np
    [sensorpos,sensorvel] = radarmotion(dt);
    [tgtpos,tgtvel] = tgtmotion(dt);
    [tgtrng,tgtang] = rangeangle(tgtpos,sensorpos);
    sig = waveform();
    [txsig,txstatus] = transmitter(sig);
    txsig = radiator(txsig,tgtang);
    txsig = channel(txsig,sensorpos,tgtpos,sensorvel,tgtvel);    
    tgtsig = target(txsig);   
    rxcol = collector(tgtsig,tgtang);
    rxsig = receiver(rxcol);
    cube(:,n) = rxsig;
end

Display the data cube containing signals per pulse.

imagesc([0:(Np-1)]*pri*1e6,[0:(Nr-1)]/fs*1e6,abs(cube))
xlabel("Slow Time {\mu}s")
ylabel("Fast Time {\mu}s")
axis xy

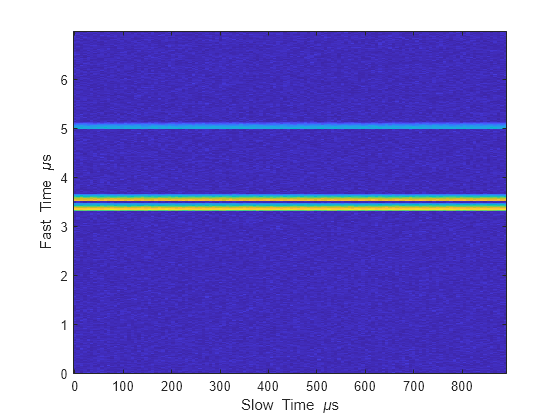
Figure contains an axes object. The axes object with xlabel Slow Time mu s, ylabel Fast Time mu s contains an object of type image.

Create and display the range-Doppler image for 128 Doppler bins. The image shows range vertically and speed horizontally. Use the linear FM waveform for match filtering. The image is here is the range-Doppler map.

ndop = 128;
rangedopresp = phased.RangeDopplerResponse(SampleRate=fs, ...
    PropagationSpeed=c,DopplerFFTLengthSource="Property", ...
    DopplerFFTLength=ndop,DopplerOutput="Speed", ...
    OperatingFrequency=fc);
matchingcoeff = getMatchedFilter(waveform);
[rngdopresp,rnggrid,dopgrid] = rangedopresp(cube,matchingcoeff);
imagesc(dopgrid,rnggrid,10*log10(abs(rngdopresp)))
xlabel("Closing Speed (m/s)")
ylabel("Range (m)")
axis xy

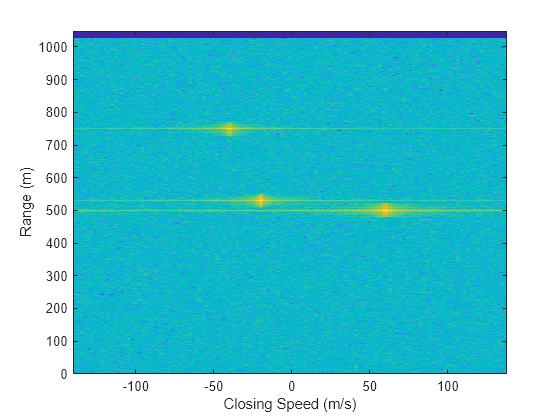
Figure contains an axes object. The axes object with xlabel Closing Speed (m/s), ylabel Range (m) contains an object of type image.

Because the targets lie along the positive x-axis, positive velocity in the global coordinate system corresponds to negative closing speed. Negative velocity in the global coordinate system corresponds to positive closing speed.

Estimate the noise power after matched filtering. Create a constant noise background image for simulation purposes.

mfgain = matchingcoeff'*matchingcoeff;
dopgain = Np;
noisebw = fs;
noisepower = noisepow(noisebw,receiver.NoiseFigure,receiver.ReferenceTemperature);
noisepowerprc = mfgain*dopgain*noisepower;
noise = noisepowerprc*ones(size(rngdopresp));

Create the range and Doppler estimator objects.

rangeestimator = phased.RangeEstimator(NumEstimatesSource="Auto", ...
    VarianceOutputPort=true,NoisePowerSource="Input port", ...
    RMSResolution=rngrms);
dopestimator = phased.DopplerEstimator(VarianceOutputPort=true, ...
    NoisePowerSource="Input port",NumPulses=Np);

Locate the target indices in the range-Doppler image. Instead of using a CFAR detector, for simplicity, use the known locations and speeds of the targets to obtain the corresponding index in the range-Doppler image.

detidx = NaN(2,Numtgts);
tgtrng = rangeangle(tgtpos,radarpos);
tgtspd = radialspeed(tgtpos,tgtvel,radarpos,radarvel);
tgtdop = 2*speed2dop(tgtspd,c/fc);
for m = 1:numel(tgtrng)
    [~,iMin] = min(abs(rnggrid-tgtrng(m)));
    detidx(1,m) = iMin;
    [~,iMin] = min(abs(dopgrid-tgtspd(m)));
    detidx(2,m) = iMin;
end

Find the noise power at the detection locations.

ind = sub2ind(size(noise),detidx(1,:),detidx(2,:));

Estimate the range and range variance at the detection locations. The estimated ranges agree with the postulated ranges.

[rngest,rngvar] = rangeestimator(rngdopresp,rnggrid,detidx,noise(ind))
rngest = 3×1

  499.7911
  529.8380
  750.0983


rngvar = 3×1
10-4 ×

    0.0273
    0.0276
    0.2094

Estimate the speed and speed variance at the detection locations. The estimated speeds agree with the predicted speeds.

[spdest,spdvar] = dopestimator(rngdopresp,dopgrid,detidx,noise(ind))
spdest = 3×1

   60.5241
  -19.6167
  -39.5838


spdvar = 3×1
10-5 ×

    0.0806
    0.0816
    0.6188

More About

expand all

Algorithms

expand all

References

[1] Richards, M. Fundamentals of Radar Signal Processing. 2nd ed. McGraw-Hill Professional Engineering, 2014.

[2] Richards, M., J. Scheer, and W. Holm. Principles of Modern Radar: Basic Principles. SciTech Publishing, 2010.

Extended Capabilities

expand all

Version History

Introduced in R2017a

See Also

Functions

Objects

Topics