cpsd
Cross power spectral density
Syntax
Description
pxy = cpsd(x,y)x and y,
using Welch’s averaged, modified periodogram method of spectral
estimation.
If
xandyare both vectors, they must have the same length.If one of the signals is a matrix and the other is a vector, then the length of the vector must equal the number of rows in the matrix. The function expands the vector and returns a matrix of column-by-column cross power spectral density estimates.
If
xandyare matrices with the same number of rows but different numbers of columns, thencpsdreturns a three-dimensional array,pxy, containing cross power spectral density estimates for all combinations of input columns. Each column ofpxycorresponds to a column ofx, and each page corresponds to a column ofy:pxy(:,m,n) = cpsd(x(:,m),y(:,n)).If
xandyare matrices of equal size, thencpsdoperates column-wise:pxy(:,n) = cpsd(x(:,n),y(:,n)). To obtain a multi-input/multi-output array, append'mimo'to the argument list.
For real x and y, cpsd returns
a one-sided CPSD. For complex x or y, cpsd returns
a two-sided CPSD.
[ returns
a vector of frequencies, pxy,f] = cpsd(___,fs)f, expressed in terms
of the sample rate, fs, at which the cross power
spectral density is estimated. fs must be the
sixth numeric input to cpsd. To input a sample
rate and still use the default values of the preceding optional arguments,
specify these arguments as empty, [].
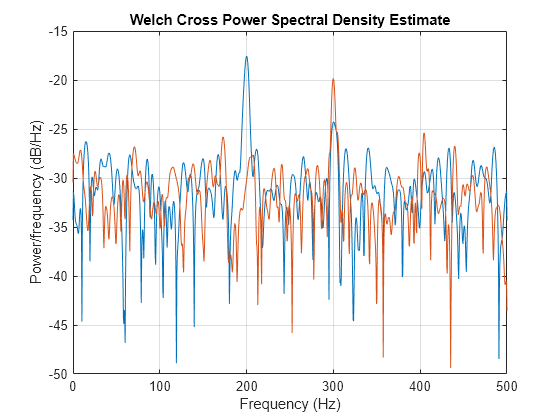
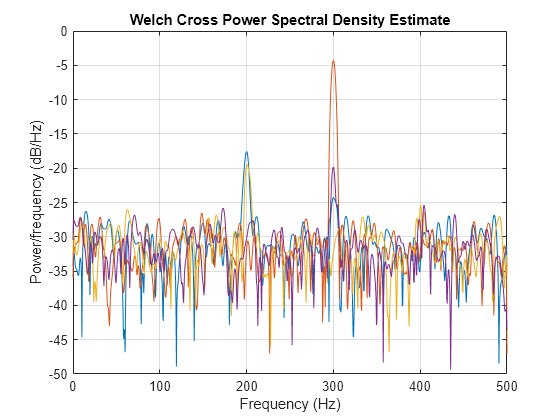
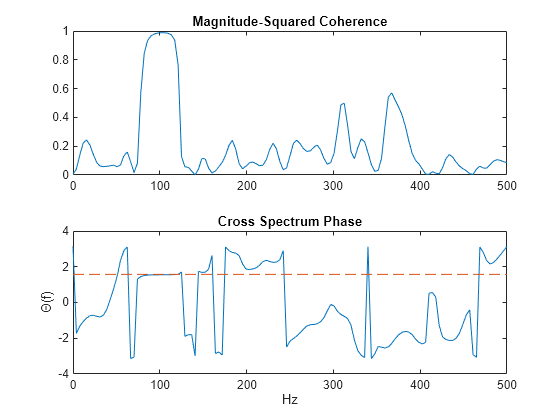
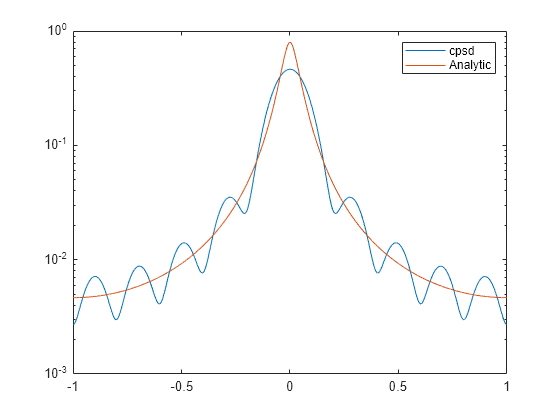
cpsd(___) with
no output arguments plots the cross power spectral density estimate
in the current figure window.
Examples
Input Arguments
Output Arguments
More About
Algorithms
cpsd uses Welch’s averaged, modified
periodogram method of spectral estimation.
References
[1] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck. Discrete-Time Signal Processing. 2nd Ed. Upper Saddle River, NJ: Prentice Hall, 1999.
[2] Rabiner, Lawrence R., and B. Gold. Theory and Application of Digital Signal Processing. Englewood Cliffs, NJ: Prentice-Hall, 1975, pp. 414–419.
[3] Welch, Peter D. “The Use of the Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging Over Short, Modified Periodograms.” IEEE® Transactions on Audio and Electroacoustics, Vol. AU-15, June 1967, pp. 70–73.