fitrauto
Automatically select regression model with optimized hyperparameters
Syntax
Description
Given predictor and response data, fitrauto automatically
tries a selection of regression model types with different hyperparameter values. By default,
the function uses Bayesian optimization to select models and their hyperparameter values, and
computes the following for each model: log(1 + valLoss), where valLoss is the cross-validation mean squared error
(MSE). After the optimization is complete, fitrauto returns the model,
trained on the entire data set, that is expected to best predict the responses for new data.
You can use the predict and loss object functions of
the returned model to predict on new data and compute the test set MSE,
respectively.
Use fitrauto when you are uncertain which model types best suit your
data. For information on alternative methods for tuning hyperparameters of regression models,
see Alternative Functionality.
If your data contains over 10,000 observations, consider using an asynchronous successive
halving algorithm (ASHA) instead of Bayesian optimization when you run
fitrauto. ASHA optimization often finds good solutions faster than
Bayesian optimization for data sets with many observations.
Mdl = fitrauto(Tbl,ResponseVarName)Mdl with tuned hyperparameters. The table
Tbl contains the predictor variables and the response variable,
where ResponseVarName is the name of the response variable.
Mdl = fitrauto(___,Name,Value)HyperparameterOptimizationOptions name-value argument to specify
whether to use Bayesian optimization (default) or an asynchronous successive halving
algorithm (ASHA). To use ASHA optimization, specify
"HyperparameterOptimizationOptions",struct("Optimizer","asha"). You
can include additional fields in the structure to control other aspects of the
optimization.
[
also returns Mdl,OptimizationResults] = fitrauto(___)OptimizationResults, which contains the results of the
model selection and hyperparameter tuning process.
Examples
Use fitrauto to automatically select a regression model with optimized hyperparameters, given predictor and response data stored in a table.
Load Data
Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s.
load carbigCreate a table containing the predictor variables Acceleration, Displacement, and so on, as well as the response variable MPG.
cars = table(Acceleration,Displacement,Horsepower, ...
Model_Year,Origin,Weight,MPG);Remove rows of cars where the table has missing values.
cars = rmmissing(cars);
Categorize the cars based on whether they were made in the USA.
cars.Origin = categorical(cellstr(cars.Origin)); cars.Origin = mergecats(cars.Origin,["France","Japan",... "Germany","Sweden","Italy","England"],"NotUSA");
Partition Data
Partition the data into training and test sets. Use approximately 80% of the observations for the model selection and hyperparameter tuning process, and 20% of the observations to test the performance of the final model returned by fitrauto. Use cvpartition to partition the data.
rng("default") % For reproducibility of the data partition c = cvpartition(height(cars),"Holdout",0.2); trainingIdx = training(c); % Training set indices carsTrain = cars(trainingIdx,:); testIdx = test(c); % Test set indices carsTest = cars(testIdx,:);
Run fitrauto
Pass the training data to fitrauto. By default, fitrauto determines appropriate model types to try, uses Bayesian optimization to find good hyperparameter values, and returns a trained model Mdl with the best expected performance. Additionally, fitrauto provides a plot of the optimization and an iterative display of the optimization results. For more information on how to interpret these results, see Verbose Display.
Expect this process to take some time. To speed up the optimization process, consider running the optimization in parallel, if you have a Parallel Computing Toolbox™ license. To do so, pass "HyperparameterOptimizationOptions",struct("UseParallel",true) to fitrauto as a name-value argument.
Mdl = fitrauto(carsTrain,"MPG");Learner types to explore: ensemble, svm, tree Total iterations (MaxObjectiveEvaluations): 90 Total time (MaxTime): Inf |================================================================================================================================================| | Iter | Eval | log(1+valLoss)| Time for training | Observed min | Estimated min | Learner | Hyperparameter: Value | | | result | | & validation (sec)| validation loss | validation loss | | | |================================================================================================================================================| | 1 | Best | 3.3416 | 0.1617 | 3.3416 | 3.3416 | tree | MinLeafSize: 118 | | 2 | Accept | 4.1303 | 0.10689 | 3.3416 | 3.3416 | svm | BoxConstraint: 16.579 | | | | | | | | | KernelScale: 0.0045538 | | | | | | | | | Epsilon: 657.79 | | 3 | Best | 2.5197 | 0.077313 | 2.5197 | 2.6121 | tree | MinLeafSize: 2 | | 4 | Best | 2.3335 | 4.6922 | 2.3335 | 2.3335 | ensemble | Method: Bag | | | | | | | | | NumLearningCycles: 291 | | | | | | | | | MinLeafSize: 9 | | 5 | Accept | 2.3398 | 3.1524 | 2.3335 | 2.3366 | ensemble | Method: Bag | | | | | | | | | NumLearningCycles: 206 | | | | | | | | | MinLeafSize: 13 | | 6 | Best | 2.204 | 4.9207 | 2.204 | 2.2049 | ensemble | Method: LSBoost | | | | | | | | | NumLearningCycles: 256 | | | | | | | | | MinLeafSize: 12 | | 7 | Accept | 4.1303 | 0.055823 | 2.204 | 2.2049 | svm | BoxConstraint: 0.0048178 | | | | | | | | | KernelScale: 0.011576 | | | | | | | | | Epsilon: 441.39 | | 8 | Accept | 2.4787 | 0.060431 | 2.204 | 2.2049 | tree | MinLeafSize: 9 | | 9 | Accept | 4.1303 | 0.03731 | 2.204 | 2.2049 | svm | BoxConstraint: 8.581 | | | | | | | | | KernelScale: 61.095 | | | | | | | | | Epsilon: 296.69 | | 10 | Accept | 4.1303 | 0.035203 | 2.204 | 2.2049 | svm | BoxConstraint: 140.96 | | | | | | | | | KernelScale: 0.012197 | | | | | | | | | Epsilon: 69.002 | | 11 | Accept | 2.9157 | 0.035004 | 2.204 | 2.2049 | tree | MinLeafSize: 32 | | 12 | Accept | 3.2199 | 0.033218 | 2.204 | 2.2049 | tree | MinLeafSize: 64 | | 13 | Accept | 2.4157 | 0.038466 | 2.204 | 2.2049 | tree | MinLeafSize: 4 | | 14 | Accept | 4.1303 | 0.039282 | 2.204 | 2.2049 | svm | BoxConstraint: 1.3859 | | | | | | | | | KernelScale: 71.061 | | | | | | | | | Epsilon: 181.44 | | 15 | Accept | 3.4156 | 0.032522 | 2.204 | 2.2049 | tree | MinLeafSize: 102 | | 16 | Accept | 2.5197 | 0.042514 | 2.204 | 2.2049 | tree | MinLeafSize: 2 | | 17 | Accept | 5.4306 | 23.255 | 2.204 | 2.2049 | svm | BoxConstraint: 0.0018102 | | | | | | | | | KernelScale: 0.016815 | | | | | | | | | Epsilon: 8.1687 | | 18 | Accept | 3.1121 | 4.0538 | 2.204 | 2.2042 | ensemble | Method: Bag | | | | | | | | | NumLearningCycles: 288 | | | | | | | | | MinLeafSize: 106 | | 19 | Best | 2.1971 | 4.4769 | 2.1971 | 2.1972 | ensemble | Method: LSBoost | | | | | | | | | NumLearningCycles: 227 | | | | | | | | | MinLeafSize: 2 | | 20 | Best | 2.1971 | 4.1893 | 2.1971 | 2.1972 | ensemble | Method: LSBoost | | | | | | | | | NumLearningCycles: 223 | | | | | | | | | MinLeafSize: 2 | |================================================================================================================================================| | Iter | Eval | log(1+valLoss)| Time for training | Observed min | Estimated min | Learner | Hyperparameter: Value | | | result | | & validation (sec)| validation loss | validation loss | | | |================================================================================================================================================| | 21 | Accept | 2.2314 | 5.0182 | 2.1971 | 2.1972 | ensemble | Method: LSBoost | | | | | | | | | NumLearningCycles: 262 | | | | | | | | | MinLeafSize: 5 | | 22 | Accept | 2.5925 | 4.2399 | 2.1971 | 2.1972 | ensemble | Method: Bag | | | | | | | | | NumLearningCycles: 283 | | | | | | | | | MinLeafSize: 39 | | 23 | Accept | 2.1971 | 5.466 | 2.1971 | 2.1972 | ensemble | Method: LSBoost | | | | | | | | | NumLearningCycles: 285 | | | | | | | | | MinLeafSize: 2 | | 24 | Accept | 2.3352 | 1.6689 | 2.1971 | 2.1972 | svm | BoxConstraint: 2.2648 | | | | | | | | | KernelScale: 0.92531 | | | | | | | | | Epsilon: 0.51865 | | 25 | Accept | 2.9882 | 3.4342 | 2.1971 | 2.1971 | ensemble | Method: Bag | | | | | | | | | NumLearningCycles: 247 | | | | | | | | | MinLeafSize: 73 | | 26 | Accept | 2.3583 | 3.7169 | 2.1971 | 2.1971 | ensemble | Method: Bag | | | | | | | | | NumLearningCycles: 255 | | | | | | | | | MinLeafSize: 12 | | 27 | Accept | 2.6476 | 0.052651 | 2.1971 | 2.1971 | tree | MinLeafSize: 28 | | 28 | Accept | 2.4016 | 0.045653 | 2.1971 | 2.1971 | tree | MinLeafSize: 6 | | 29 | Accept | 3.7573 | 0.054446 | 2.1971 | 2.1971 | svm | BoxConstraint: 9.4057 | | | | | | | | | KernelScale: 100.66 | | | | | | | | | Epsilon: 0.24447 | | 30 | Accept | 2.6046 | 0.038702 | 2.1971 | 2.1971 | tree | MinLeafSize: 24 | | 31 | Accept | 2.4157 | 0.038974 | 2.1971 | 2.1971 | tree | MinLeafSize: 4 | | 32 | Accept | 4.1303 | 0.034693 | 2.1971 | 2.1971 | svm | BoxConstraint: 303.85 | | | | | | | | | KernelScale: 0.0083624 | | | | | | | | | Epsilon: 39.54 | | 33 | Accept | 4.146 | 0.039632 | 2.1971 | 2.1971 | svm | BoxConstraint: 0.16546 | | | | | | | | | KernelScale: 248.79 | | | | | | | | | Epsilon: 1.1182 | | 34 | Accept | 3.0466 | 0.035622 | 2.1971 | 2.1971 | tree | MinLeafSize: 46 | | 35 | Accept | 2.3417 | 3.6854 | 2.1971 | 2.1971 | ensemble | Method: Bag | | | | | | | | | NumLearningCycles: 246 | | | | | | | | | MinLeafSize: 12 | | 36 | Accept | 2.7264 | 5.237 | 2.1971 | 2.1972 | ensemble | Method: LSBoost | | | | | | | | | NumLearningCycles: 274 | | | | | | | | | MinLeafSize: 105 | | 37 | Accept | 2.5457 | 3.608 | 2.1971 | 2.1972 | ensemble | Method: Bag | | | | | | | | | NumLearningCycles: 257 | | | | | | | | | MinLeafSize: 33 | | 38 | Accept | 2.6603 | 0.057475 | 2.1971 | 2.1972 | tree | MinLeafSize: 1 | | 39 | Accept | 2.3589 | 2.9631 | 2.1971 | 2.1972 | svm | BoxConstraint: 56.509 | | | | | | | | | KernelScale: 1.509 | | | | | | | | | Epsilon: 0.5604 | | 40 | Accept | 4.1303 | 0.037567 | 2.1971 | 2.1972 | svm | BoxConstraint: 0.001484 | | | | | | | | | KernelScale: 0.0032176 | | | | | | | | | Epsilon: 22.445 | |================================================================================================================================================| | Iter | Eval | log(1+valLoss)| Time for training | Observed min | Estimated min | Learner | Hyperparameter: Value | | | result | | & validation (sec)| validation loss | validation loss | | | |================================================================================================================================================| | 41 | Accept | 2.5507 | 0.045858 | 2.1971 | 2.1972 | tree | MinLeafSize: 15 | | 42 | Best | 2.1945 | 5.5104 | 2.1945 | 2.1966 | ensemble | Method: LSBoost | | | | | | | | | NumLearningCycles: 289 | | | | | | | | | MinLeafSize: 6 | | 43 | Accept | 3.9788 | 0.050732 | 2.1945 | 2.1966 | svm | BoxConstraint: 31.423 | | | | | | | | | KernelScale: 0.16609 | | | | | | | | | Epsilon: 14.619 | | 44 | Accept | 4.0639 | 0.040411 | 2.1945 | 2.1966 | svm | BoxConstraint: 42.958 | | | | | | | | | KernelScale: 459.03 | | | | | | | | | Epsilon: 0.98679 | | 45 | Accept | 2.5392 | 0.037327 | 2.1945 | 2.1966 | svm | BoxConstraint: 32.844 | | | | | | | | | KernelScale: 24.244 | | | | | | | | | Epsilon: 2.8938 | | 46 | Accept | 4.1222 | 0.039989 | 2.1945 | 2.1966 | svm | BoxConstraint: 0.001348 | | | | | | | | | KernelScale: 5.1158 | | | | | | | | | Epsilon: 2.4534 | | 47 | Best | 2.1523 | 0.054429 | 2.1523 | 2.1525 | svm | BoxConstraint: 145.8 | | | | | | | | | KernelScale: 6.9661 | | | | | | | | | Epsilon: 1.692 | | 48 | Best | 2.0991 | 0.043964 | 2.0991 | 2.0991 | svm | BoxConstraint: 11.118 | | | | | | | | | KernelScale: 4.5614 | | | | | | | | | Epsilon: 0.6909 | | 49 | Accept | 2.1321 | 0.048682 | 2.0991 | 2.0991 | svm | BoxConstraint: 12.625 | | | | | | | | | KernelScale: 3.7951 | | | | | | | | | Epsilon: 1.9243 | | 50 | Accept | 2.1155 | 0.065734 | 2.0991 | 2.0988 | svm | BoxConstraint: 2.9811 | | | | | | | | | KernelScale: 2.2304 | | | | | | | | | Epsilon: 0.11742 | | 51 | Accept | 2.1127 | 0.061163 | 2.0991 | 2.0991 | svm | BoxConstraint: 4.6122 | | | | | | | | | KernelScale: 2.5002 | | | | | | | | | Epsilon: 0.24122 | | 52 | Accept | 2.3111 | 2.183 | 2.0991 | 2.099 | svm | BoxConstraint: 13.002 | | | | | | | | | KernelScale: 1.2194 | | | | | | | | | Epsilon: 0.0097793 | | 53 | Accept | 2.1329 | 0.060156 | 2.0991 | 2.0987 | svm | BoxConstraint: 81.429 | | | | | | | | | KernelScale: 5.9963 | | | | | | | | | Epsilon: 0.040814 | | 54 | Accept | 2.1395 | 0.046864 | 2.0991 | 2.0991 | svm | BoxConstraint: 43.058 | | | | | | | | | KernelScale: 8.8124 | | | | | | | | | Epsilon: 0.31232 | | 55 | Accept | 2.1268 | 0.070321 | 2.0991 | 2.0993 | svm | BoxConstraint: 18.909 | | | | | | | | | KernelScale: 3.2821 | | | | | | | | | Epsilon: 0.049352 | | 56 | Accept | 2.2052 | 5.7654 | 2.0991 | 2.0993 | ensemble | Method: LSBoost | | | | | | | | | NumLearningCycles: 299 | | | | | | | | | MinLeafSize: 1 | | 57 | Accept | 2.1528 | 0.15163 | 2.0991 | 2.0994 | svm | BoxConstraint: 930.08 | | | | | | | | | KernelScale: 7.7684 | | | | | | | | | Epsilon: 0.15953 | | 58 | Accept | 2.1402 | 0.075441 | 2.0991 | 2.0998 | svm | BoxConstraint: 90.458 | | | | | | | | | KernelScale: 4.8465 | | | | | | | | | Epsilon: 0.16486 | | 59 | Accept | 2.169 | 0.33792 | 2.0991 | 2.0998 | svm | BoxConstraint: 838.56 | | | | | | | | | KernelScale: 4.9126 | | | | | | | | | Epsilon: 0.010297 | | 60 | Accept | 2.1441 | 0.1108 | 2.0991 | 2.1 | svm | BoxConstraint: 977.44 | | | | | | | | | KernelScale: 9.5442 | | | | | | | | | Epsilon: 0.0096251 | |================================================================================================================================================| | Iter | Eval | log(1+valLoss)| Time for training | Observed min | Estimated min | Learner | Hyperparameter: Value | | | result | | & validation (sec)| validation loss | validation loss | | | |================================================================================================================================================| | 61 | Accept | 2.3548 | 3.0057 | 2.0991 | 2.1 | ensemble | Method: Bag | | | | | | | | | NumLearningCycles: 201 | | | | | | | | | MinLeafSize: 1 | | 62 | Accept | 2.134 | 0.051302 | 2.0991 | 2.1 | svm | BoxConstraint: 7.3349 | | | | | | | | | KernelScale: 4.5654 | | | | | | | | | Epsilon: 0.010146 | | 63 | Accept | 2.1198 | 0.042744 | 2.0991 | 2.1015 | svm | BoxConstraint: 9.5959 | | | | | | | | | KernelScale: 4.8771 | | | | | | | | | Epsilon: 0.19667 | | 64 | Accept | 2.1389 | 0.058507 | 2.0991 | 2.1014 | svm | BoxConstraint: 948.83 | | | | | | | | | KernelScale: 16.462 | | | | | | | | | Epsilon: 0.47562 | | 65 | Accept | 2.1122 | 0.062182 | 2.0991 | 2.1017 | svm | BoxConstraint: 1.8061 | | | | | | | | | KernelScale: 2.0447 | | | | | | | | | Epsilon: 0.010408 | | 66 | Accept | 2.1239 | 0.053398 | 2.0991 | 2.102 | svm | BoxConstraint: 3.1375 | | | | | | | | | KernelScale: 2.5109 | | | | | | | | | Epsilon: 0.012724 | | 67 | Accept | 2.1168 | 0.051692 | 2.0991 | 2.104 | svm | BoxConstraint: 15.336 | | | | | | | | | KernelScale: 3.8639 | | | | | | | | | Epsilon: 0.35151 | | 68 | Accept | 2.1262 | 0.060441 | 2.0991 | 2.1042 | svm | BoxConstraint: 619.86 | | | | | | | | | KernelScale: 12.746 | | | | | | | | | Epsilon: 0.12944 | | 69 | Accept | 2.1288 | 0.041367 | 2.0991 | 2.1087 | svm | BoxConstraint: 14.346 | | | | | | | | | KernelScale: 5.6377 | | | | | | | | | Epsilon: 1.1115 | | 70 | Accept | 2.1075 | 0.046906 | 2.0991 | 2.1073 | svm | BoxConstraint: 6.3065 | | | | | | | | | KernelScale: 3.3652 | | | | | | | | | Epsilon: 0.37711 | | 71 | Accept | 2.1122 | 0.058036 | 2.0991 | 2.1071 | svm | BoxConstraint: 0.21669 | | | | | | | | | KernelScale: 1.3771 | | | | | | | | | Epsilon: 0.010668 | | 72 | Accept | 2.1086 | 0.057236 | 2.0991 | 2.1072 | svm | BoxConstraint: 0.6199 | | | | | | | | | KernelScale: 1.6673 | | | | | | | | | Epsilon: 0.02609 | | 73 | Accept | 2.2008 | 0.20609 | 2.0991 | 2.107 | svm | BoxConstraint: 0.74478 | | | | | | | | | KernelScale: 1.1364 | | | | | | | | | Epsilon: 0.0097464 | | 74 | Accept | 2.1274 | 0.045525 | 2.0991 | 2.1075 | svm | BoxConstraint: 0.24664 | | | | | | | | | KernelScale: 1.9581 | | | | | | | | | Epsilon: 0.0095196 | | 75 | Accept | 2.1194 | 0.062398 | 2.0991 | 2.1076 | svm | BoxConstraint: 0.84673 | | | | | | | | | KernelScale: 1.6712 | | | | | | | | | Epsilon: 0.38722 | | 76 | Accept | 2.339 | 3.0245 | 2.0991 | 2.1076 | ensemble | Method: Bag | | | | | | | | | NumLearningCycles: 204 | | | | | | | | | MinLeafSize: 3 | | 77 | Accept | 4.1303 | 0.045681 | 2.0991 | 2.1046 | svm | BoxConstraint: 3.6938 | | | | | | | | | KernelScale: 1.3489 | | | | | | | | | Epsilon: 883.83 | | 78 | Accept | 2.1418 | 0.063846 | 2.0991 | 2.105 | svm | BoxConstraint: 53.966 | | | | | | | | | KernelScale: 4.7398 | | | | | | | | | Epsilon: 0.0098142 | | 79 | Accept | 2.1226 | 0.068867 | 2.0991 | 2.1052 | svm | BoxConstraint: 0.21684 | | | | | | | | | KernelScale: 1.2724 | | | | | | | | | Epsilon: 0.067508 | | 80 | Accept | 2.1215 | 0.071022 | 2.0991 | 2.1054 | svm | BoxConstraint: 0.89132 | | | | | | | | | KernelScale: 1.6131 | | | | | | | | | Epsilon: 0.080329 | |================================================================================================================================================| | Iter | Eval | log(1+valLoss)| Time for training | Observed min | Estimated min | Learner | Hyperparameter: Value | | | result | | & validation (sec)| validation loss | validation loss | | | |================================================================================================================================================| | 81 | Accept | 2.1109 | 0.049506 | 2.0991 | 2.1055 | svm | BoxConstraint: 1.8778 | | | | | | | | | KernelScale: 2.3249 | | | | | | | | | Epsilon: 0.40345 | | 82 | Accept | 2.1894 | 0.047319 | 2.0991 | 2.1052 | svm | BoxConstraint: 0.0080677 | | | | | | | | | KernelScale: 0.98345 | | | | | | | | | Epsilon: 0.0098795 | | 83 | Accept | 2.1159 | 0.055132 | 2.0991 | 2.1053 | svm | BoxConstraint: 0.097667 | | | | | | | | | KernelScale: 1.4607 | | | | | | | | | Epsilon: 0.029531 | | 84 | Accept | 2.1106 | 0.047832 | 2.0991 | 2.1064 | svm | BoxConstraint: 9.7081 | | | | | | | | | KernelScale: 3.5404 | | | | | | | | | Epsilon: 0.77633 | | 85 | Accept | 2.1338 | 0.052769 | 2.0991 | 2.1065 | svm | BoxConstraint: 328.02 | | | | | | | | | KernelScale: 11.996 | | | | | | | | | Epsilon: 0.63786 | | 86 | Accept | 2.1017 | 0.046959 | 2.0991 | 2.1033 | svm | BoxConstraint: 15.397 | | | | | | | | | KernelScale: 4.4256 | | | | | | | | | Epsilon: 0.7265 | | 87 | Accept | 4.1303 | 0.036522 | 2.0991 | 2.1033 | svm | BoxConstraint: 434.58 | | | | | | | | | KernelScale: 0.0010827 | | | | | | | | | Epsilon: 0.011393 | | 88 | Accept | 2.0996 | 0.046978 | 2.0991 | 2.1017 | svm | BoxConstraint: 24.978 | | | | | | | | | KernelScale: 4.7899 | | | | | | | | | Epsilon: 0.72324 | | 89 | Accept | 2.1053 | 0.046511 | 2.0991 | 2.1025 | svm | BoxConstraint: 18.777 | | | | | | | | | KernelScale: 4.5251 | | | | | | | | | Epsilon: 0.76878 | | 90 | Accept | 2.1034 | 0.047849 | 2.0991 | 2.1026 | svm | BoxConstraint: 19.098 | | | | | | | | | KernelScale: 4.5336 | | | | | | | | | Epsilon: 0.75174 | __________________________________________________________ Optimization completed. Total iterations: 90 Total elapsed time: 136.2822 seconds Total time for training and validation: 111.4242 seconds Best observed learner is an svm model with: Learner: svm BoxConstraint: 11.118 KernelScale: 4.5614 Epsilon: 0.6909 Observed log(1 + valLoss): 2.0991 Time for training and validation: 0.043964 seconds Best estimated learner (returned model) is an svm model with: Learner: svm BoxConstraint: 15.397 KernelScale: 4.4256 Epsilon: 0.7265 Estimated log(1 + valLoss): 2.1026 Estimated time for training and validation: 0.046399 seconds Documentation for fitrauto display
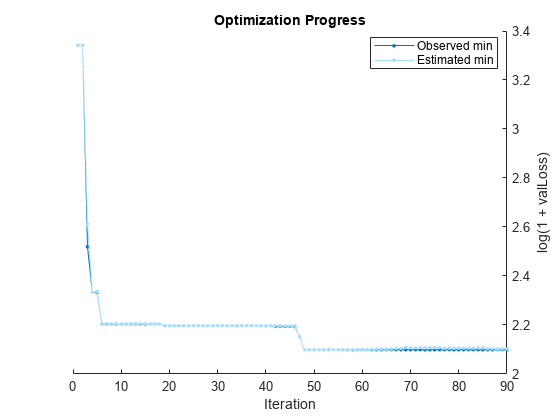
The final model returned by fitrauto corresponds to the best estimated learner. Before returning the model, the function retrains it using the entire training data (carsTrain), the listed Learner (or model) type, and the displayed hyperparameter values.
Evaluate Test Set Performance
Evaluate the performance of the model on the test set. testError is based on the test set mean squared error (MSE). Smaller MSE values indicate better performance.
testMSE = loss(Mdl,carsTest,"MPG");
testError = log(1 + testMSE)testError = 2.2000
Use fitrauto to automatically select a regression model with optimized hyperparameters, given predictor and response data stored in separate variables.
Load Data
Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s.
load carbigCreate a matrix X containing the predictor variables Acceleration, Cylinders, and so on. Store the response variable MPG in the variable Y.
X = [Acceleration Cylinders Displacement Weight]; Y = MPG;
Delete rows of X and Y where either array has missing values.
R = rmmissing([X Y]); X = R(:,1:end-1); Y = R(:,end);
Create a variable indicating which predictors are categorical. Cylinders is the only categorical variable in X.
categoricalVars = [false true false false];
Partition Data
Partition the data into training and test sets. Use approximately 80% of the observations for the model selection and hyperparameter tuning process, and 20% of the observations to test the performance of the final model returned by fitrauto. Use cvpartition to partition the data.
rng("default") % For reproducibility of the partition c = cvpartition(length(Y),"Holdout",0.20); trainingIdx = training(c); % Indices for the training set XTrain = X(trainingIdx,:); YTrain = Y(trainingIdx); testIdx = test(c); % Indices for the test set XTest = X(testIdx,:); YTest = Y(testIdx);
Run fitrauto
Pass the training data to fitrauto. By default, fitrauto determines appropriate model (or learner) types to try, uses Bayesian optimization to find good hyperparameter values for those models, and returns a trained model Mdl with the best expected performance. Specify the categorical predictors, and run the optimization in parallel (requires Parallel Computing Toolbox™). Return a second output OptimizationResults that contains the details of the Bayesian optimization.
Expect this process to take some time. By default, fitrauto provides a plot of the optimization and an iterative display of the optimization results. For more information on how to interpret these results, see Verbose Display.
options = struct("UseParallel",true); [Mdl,OptimizationResults] = fitrauto(XTrain,YTrain, ... "CategoricalPredictors",categoricalVars, ... "HyperparameterOptimizationOptions",options);
Starting parallel pool (parpool) using the 'Processes' profile ... Connected to parallel pool with 8 workers. Copying objective function to workers... Done copying objective function to workers. Learner types to explore: ensemble, svm, tree Total iterations (MaxObjectiveEvaluations): 90 Total time (MaxTime): Inf |==========================================================================================================================================================| | Iter | Active | Eval | log(1+valLoss)| Time for training | Observed min | Estimated min | Learner | Hyperparameter: Value | | | workers | result | | & validation (sec)| validation loss | validation loss | | | |==========================================================================================================================================================| | 1 | 6 | Best | 3.1329 | 1.9788 | 3.1329 | 3.1329 | tree | MinLeafSize: 5 | | 2 | 6 | Accept | 3.1329 | 1.985 | 3.1329 | 3.1329 | tree | MinLeafSize: 5 | | 3 | 6 | Accept | 3.1539 | 1.9764 | 3.1329 | 3.1329 | tree | MinLeafSize: 9 | | 4 | 6 | Accept | 4.1701 | 2.1518 | 3.1329 | 3.1329 | svm | BoxConstraint: 0.033502 | | | | | | | | | | KernelScale: 153.38 | | | | | | | | | | Epsilon: 0.095234 | | 5 | 8 | Accept | 3.1684 | 0.72622 | 3.1329 | 3.147 | tree | MinLeafSize: 4 | | 6 | 8 | Best | 3.0322 | 0.20501 | 3.0322 | 3.0528 | svm | BoxConstraint: 0.010812 | | | | | | | | | | KernelScale: 1.2015 | | | | | | | | | | Epsilon: 0.034779 | | 7 | 8 | Accept | 3.2871 | 0.23632 | 3.0322 | 3.0528 | tree | MinLeafSize: 2 | | 8 | 8 | Accept | 4.1645 | 7.601 | 3.0322 | 3.0528 | ensemble | Method: Bag | | | | | | | | | | NumLearningCycles: 257 | | | | | | | | | | MinLeafSize: 154 | | 9 | 8 | Accept | 3.2871 | 0.50364 | 3.0322 | 3.0528 | tree | MinLeafSize: 2 | | 10 | 8 | Best | 2.9469 | 10.828 | 2.9469 | 2.9628 | ensemble | Method: LSBoost | | | | | | | | | | NumLearningCycles: 287 | | | | | | | | | | MinLeafSize: 1 | | 11 | 8 | Best | 2.9388 | 10.949 | 2.9388 | 2.9413 | ensemble | Method: LSBoost | | | | | | | | | | NumLearningCycles: 288 | | | | | | | | | | MinLeafSize: 3 | | 12 | 8 | Accept | 2.9581 | 10.32 | 2.9388 | 2.9404 | ensemble | Method: LSBoost | | | | | | | | | | NumLearningCycles: 287 | | | | | | | | | | MinLeafSize: 62 | | 13 | 7 | Accept | 2.9581 | 10.584 | 2.9388 | 2.9403 | ensemble | Method: LSBoost | | | | | | | | | | NumLearningCycles: 287 | | | | | | | | | | MinLeafSize: 62 | | 14 | 7 | Accept | 2.9581 | 10.626 | 2.9388 | 2.9403 | ensemble | Method: LSBoost | | | | | | | | | | NumLearningCycles: 287 | | | | | | | | | | MinLeafSize: 62 | | 15 | 8 | Accept | 3.6004 | 0.36596 | 2.9388 | 2.9403 | tree | MinLeafSize: 120 | | 16 | 8 | Accept | 3.6004 | 0.41888 | 2.9388 | 2.9403 | tree | MinLeafSize: 120 | | 17 | 8 | Accept | 3.1539 | 0.14494 | 2.9388 | 2.9403 | tree | MinLeafSize: 9 | | 18 | 7 | Best | 2.9287 | 11.356 | 2.9287 | 2.9403 | ensemble | Method: LSBoost | | | | | | | | | | NumLearningCycles: 283 | | | | | | | | | | MinLeafSize: 16 | | 19 | 7 | Accept | 4.1645 | 1.9545 | 2.9287 | 2.9403 | svm | BoxConstraint: 159.44 | | | | | | | | | | KernelScale: 34.732 | | | | | | | | | | Epsilon: 412.2 | | 20 | 7 | Accept | 4.1862 | 0.1901 | 2.9287 | 2.9403 | svm | BoxConstraint: 7.487 | | | | | | | | | | KernelScale: 81.753 | | | | | | | | | | Epsilon: 12.782 | |==========================================================================================================================================================| | Iter | Active | Eval | log(1+valLoss)| Time for training | Observed min | Estimated min | Learner | Hyperparameter: Value | | | workers | result | | & validation (sec)| validation loss | validation loss | | | |==========================================================================================================================================================| | 21 | 7 | Accept | 4.1645 | 0.19246 | 2.9287 | 2.9403 | svm | BoxConstraint: 2.1296 | | | | | | | | | | KernelScale: 3.2623 | | | | | | | | | | Epsilon: 609.61 | | 22 | 6 | Accept | 3.9011 | 1.5706 | 2.9287 | 2.9403 | svm | BoxConstraint: 9.4057 | | | | | | | | | | KernelScale: 100.66 | | | | | | | | | | Epsilon: 0.2386 | | 23 | 6 | Accept | 3.1593 | 0.18031 | 2.9287 | 2.9403 | tree | MinLeafSize: 8 | | 24 | 7 | Accept | 2.9494 | 0.3265 | 2.9287 | 2.9403 | svm | BoxConstraint: 746.54 | | | | | | | | | | KernelScale: 5.6788 | | | | | | | | | | Epsilon: 1.0177 | | 25 | 7 | Accept | 2.9494 | 0.26551 | 2.9287 | 2.9403 | svm | BoxConstraint: 746.54 | | | | | | | | | | KernelScale: 5.6788 | | | | | | | | | | Epsilon: 1.0177 | | 26 | 7 | Accept | 9.5074 | 20.334 | 2.9287 | 2.9403 | svm | BoxConstraint: 336.91 | | | | | | | | | | KernelScale: 0.0018275 | | | | | | | | | | Epsilon: 0.10919 | | 27 | 7 | Accept | 2.9494 | 0.79583 | 2.9287 | 2.9403 | svm | BoxConstraint: 746.54 | | | | | | | | | | KernelScale: 5.6788 | | | | | | | | | | Epsilon: 1.0177 | | 28 | 6 | Best | 2.9287 | 11.352 | 2.9287 | 2.9403 | ensemble | Method: LSBoost | | | | | | | | | | NumLearningCycles: 262 | | | | | | | | | | MinLeafSize: 5 | | 29 | 6 | Accept | 3.6021 | 0.45991 | 2.9287 | 2.9403 | tree | MinLeafSize: 1 | | 30 | 5 | Accept | 3.1697 | 8.5532 | 2.9287 | 2.9403 | ensemble | Method: Bag | | | | | | | | | | NumLearningCycles: 247 | | | | | | | | | | MinLeafSize: 74 | | 31 | 5 | Accept | 3.1014 | 1.3678 | 2.9287 | 2.9403 | tree | MinLeafSize: 13 | | 32 | 8 | Accept | 2.9806 | 0.26062 | 2.9287 | 2.9403 | svm | BoxConstraint: 5.2568 | | | | | | | | | | KernelScale: 10.811 | | | | | | | | | | Epsilon: 0.074584 | | 33 | 8 | Accept | 4.165 | 0.13934 | 2.9287 | 2.9403 | svm | BoxConstraint: 0.18243 | | | | | | | | | | KernelScale: 128.12 | | | | | | | | | | Epsilon: 5.0924 | | 34 | 8 | Accept | 2.9351 | 11.473 | 2.9287 | 2.9288 | ensemble | Method: LSBoost | | | | | | | | | | NumLearningCycles: 282 | | | | | | | | | | MinLeafSize: 2 | | 35 | 7 | Accept | 2.9423 | 5.5429 | 2.9287 | 2.9288 | ensemble | Method: LSBoost | | | | | | | | | | NumLearningCycles: 202 | | | | | | | | | | MinLeafSize: 50 | | 36 | 7 | Accept | 3.4421 | 0.51292 | 2.9287 | 2.9288 | tree | MinLeafSize: 76 | | 37 | 8 | Accept | 2.9423 | 6.4536 | 2.9287 | 2.927 | ensemble | Method: LSBoost | | | | | | | | | | NumLearningCycles: 239 | | | | | | | | | | MinLeafSize: 50 | | 38 | 4 | Accept | 3.1708 | 10.551 | 2.8874 | 2.8928 | ensemble | Method: LSBoost | | | | | | | | | | NumLearningCycles: 274 | | | | | | | | | | MinLeafSize: 106 | | 39 | 4 | Accept | 2.9338 | 9.5391 | 2.8874 | 2.8928 | ensemble | Method: Bag | | | | | | | | | | NumLearningCycles: 280 | | | | | | | | | | MinLeafSize: 45 | | 40 | 4 | Accept | 2.9351 | 6.3776 | 2.8874 | 2.8928 | ensemble | Method: LSBoost | | | | | | | | | | NumLearningCycles: 233 | | | | | | | | | | MinLeafSize: 2 | |==========================================================================================================================================================| | Iter | Active | Eval | log(1+valLoss)| Time for training | Observed min | Estimated min | Learner | Hyperparameter: Value | | | workers | result | | & validation (sec)| validation loss | validation loss | | | |==========================================================================================================================================================| | 41 | 4 | Best | 2.8874 | 6.3082 | 2.8874 | 2.8928 | ensemble | Method: Bag | | | | | | | | | | NumLearningCycles: 271 | | | | | | | | | | MinLeafSize: 1 | | 42 | 4 | Accept | 2.8981 | 7.7345 | 2.8874 | 2.8928 | ensemble | Method: Bag | | | | | | | | | | NumLearningCycles: 271 | | | | | | | | | | MinLeafSize: 1 | | 43 | 8 | Accept | 3.2678 | 0.19997 | 2.8874 | 2.8928 | tree | MinLeafSize: 65 | | 44 | 5 | Best | 2.8796 | 4.3397 | 2.8796 | 2.8796 | ensemble | Method: Bag | | | | | | | | | | NumLearningCycles: 209 | | | | | | | | | | MinLeafSize: 4 | | 45 | 5 | Accept | 2.8803 | 5.559 | 2.8796 | 2.8796 | ensemble | Method: Bag | | | | | | | | | | NumLearningCycles: 250 | | | | | | | | | | MinLeafSize: 10 | | 46 | 5 | Accept | 3.2871 | 0.40833 | 2.8796 | 2.8796 | tree | MinLeafSize: 2 | | 47 | 5 | Accept | 2.9099 | 5.7828 | 2.8796 | 2.8796 | ensemble | Method: LSBoost | | | | | | | | | | NumLearningCycles: 213 | | | | | | | | | | MinLeafSize: 10 | | 48 | 8 | Accept | 2.9351 | 7.025 | 2.8796 | 2.8796 | ensemble | Method: LSBoost | | | | | | | | | | NumLearningCycles: 265 | | | | | | | | | | MinLeafSize: 2 | | 49 | 6 | Accept | 5.4316 | 20.005 | 2.8796 | 2.8796 | svm | BoxConstraint: 28.808 | | | | | | | | | | KernelScale: 0.3219 | | | | | | | | | | Epsilon: 0.13762 | | 50 | 6 | Accept | 3.1177 | 0.68844 | 2.8796 | 2.8796 | svm | BoxConstraint: 127.48 | | | | | | | | | | KernelScale: 105 | | | | | | | | | | Epsilon: 0.58941 | | 51 | 6 | Accept | 7.8524 | 0.68066 | 2.8796 | 2.8796 | svm | BoxConstraint: 3.2128 | | | | | | | | | | KernelScale: 0.0015524 | | | | | | | | | | Epsilon: 0.11513 | | 52 | 7 | Accept | 3.1329 | 0.068468 | 2.8796 | 2.8796 | tree | MinLeafSize: 5 | | 53 | 7 | Accept | 2.9597 | 0.088717 | 2.8796 | 2.8796 | svm | BoxConstraint: 990.41 | | | | | | | | | | KernelScale: 29.533 | | | | | | | | | | Epsilon: 0.015011 | | 54 | 8 | Accept | 2.9076 | 5.4054 | 2.8796 | 2.8796 | ensemble | Method: LSBoost | | | | | | | | | | NumLearningCycles: 248 | | | | | | | | | | MinLeafSize: 13 | | 55 | 8 | Accept | 4.1645 | 0.07993 | 2.8796 | 2.8796 | svm | BoxConstraint: 1.246 | | | | | | | | | | KernelScale: 0.048145 | | | | | | | | | | Epsilon: 337.42 | | 56 | 4 | Accept | 4.8948 | 27.255 | 2.8796 | 2.8796 | svm | BoxConstraint: 0.093799 | | | | | | | | | | KernelScale: 0.0053728 | | | | | | | | | | Epsilon: 17.621 | | 57 | 4 | Accept | 2.9227 | 8.5858 | 2.8796 | 2.8796 | ensemble | Method: LSBoost | | | | | | | | | | NumLearningCycles: 360 | | | | | | | | | | MinLeafSize: 9 | | 58 | 4 | Accept | 2.8934 | 5.1523 | 2.8796 | 2.8796 | ensemble | Method: Bag | | | | | | | | | | NumLearningCycles: 298 | | | | | | | | | | MinLeafSize: 2 | | 59 | 4 | Accept | 2.8877 | 5.7141 | 2.8796 | 2.8796 | ensemble | Method: Bag | | | | | | | | | | NumLearningCycles: 299 | | | | | | | | | | MinLeafSize: 2 | | 60 | 4 | Accept | 2.8982 | 5.5545 | 2.8796 | 2.8796 | ensemble | Method: Bag | | | | | | | | | | NumLearningCycles: 320 | | | | | | | | | | MinLeafSize: 1 | |==========================================================================================================================================================| | Iter | Active | Eval | log(1+valLoss)| Time for training | Observed min | Estimated min | Learner | Hyperparameter: Value | | | workers | result | | & validation (sec)| validation loss | validation loss | | | |==========================================================================================================================================================| | 61 | 8 | Accept | 3.0945 | 0.065636 | 2.8796 | 2.8796 | tree | MinLeafSize: 11 | | 62 | 6 | Accept | 2.8818 | 5.1985 | 2.8796 | 2.8796 | ensemble | Method: Bag | | | | | | | | | | NumLearningCycles: 298 | | | | | | | | | | MinLeafSize: 2 | | 63 | 6 | Accept | 4.1645 | 0.17235 | 2.8796 | 2.8796 | svm | BoxConstraint: 0.0010273 | | | | | | | | | | KernelScale: 0.24074 | | | | | | | | | | Epsilon: 280.24 | | 64 | 6 | Accept | 4.1645 | 0.069883 | 2.8796 | 2.8796 | svm | BoxConstraint: 2.4541 | | | | | | | | | | KernelScale: 5.0059 | | | | | | | | | | Epsilon: 29.021 | | 65 | 6 | Best | 2.8788 | 3.2047 | 2.8788 | 2.8785 | ensemble | Method: Bag | | | | | | | | | | NumLearningCycles: 223 | | | | | | | | | | MinLeafSize: 5 | | 66 | 6 | Accept | 3.1966 | 4.5298 | 2.8788 | 2.8785 | ensemble | Method: LSBoost | | | | | | | | | | NumLearningCycles: 243 | | | | | | | | | | MinLeafSize: 109 | | 67 | 6 | Accept | 4.2278 | 0.075829 | 2.8788 | 2.8785 | svm | BoxConstraint: 0.49855 | | | | | | | | | | KernelScale: 822.57 | | | | | | | | | | Epsilon: 13.604 | | 68 | 7 | Accept | 3.4183 | 0.040748 | 2.8788 | 2.8785 | tree | MinLeafSize: 93 | | 69 | 7 | Accept | 2.9682 | 0.089978 | 2.8788 | 2.8785 | svm | BoxConstraint: 990.82 | | | | | | | | | | KernelScale: 32.258 | | | | | | | | | | Epsilon: 0.65013 | | 70 | 7 | Accept | 17.606 | 16.61 | 2.8788 | 2.8785 | svm | BoxConstraint: 244.81 | | | | | | | | | | KernelScale: 0.029911 | | | | | | | | | | Epsilon: 1.3663 | | 71 | 7 | Accept | 3.2871 | 0.12707 | 2.8788 | 2.8785 | tree | MinLeafSize: 2 | | 72 | 6 | Accept | 2.8957 | 2.8051 | 2.8788 | 2.8785 | ensemble | Method: Bag | | | | | | | | | | NumLearningCycles: 203 | | | | | | | | | | MinLeafSize: 21 | | 73 | 6 | Accept | 4.1645 | 0.049095 | 2.8788 | 2.8785 | svm | BoxConstraint: 0.0023954 | | | | | | | | | | KernelScale: 0.0017894 | | | | | | | | | | Epsilon: 779.82 | | 74 | 7 | Accept | 4.1645 | 0.073002 | 2.8788 | 2.8785 | svm | BoxConstraint: 0.0022454 | | | | | | | | | | KernelScale: 1.2218 | | | | | | | | | | Epsilon: 1223.3 | | 75 | 6 | Accept | 3.0324 | 7.4797 | 2.8788 | 2.878 | ensemble | Method: LSBoost | | | | | | | | | | NumLearningCycles: 386 | | | | | | | | | | MinLeafSize: 74 | | 76 | 6 | Accept | 2.8964 | 3.1304 | 2.8788 | 2.878 | ensemble | Method: Bag | | | | | | | | | | NumLearningCycles: 222 | | | | | | | | | | MinLeafSize: 21 | | 77 | 6 | Accept | 3.1637 | 0.054723 | 2.8788 | 2.878 | tree | MinLeafSize: 6 | | 78 | 5 | Accept | 2.8986 | 2.8386 | 2.8788 | 2.878 | ensemble | Method: Bag | | | | | | | | | | NumLearningCycles: 204 | | | | | | | | | | MinLeafSize: 21 | | 79 | 5 | Accept | 4.1645 | 0.04896 | 2.8788 | 2.878 | svm | BoxConstraint: 0.0012664 | | | | | | | | | | KernelScale: 0.0010838 | | | | | | | | | | Epsilon: 54.909 | | 80 | 7 | Accept | 16.812 | 11.246 | 2.8788 | 2.8778 | svm | BoxConstraint: 0.071974 | | | | | | | | | | KernelScale: 0.030156 | | | | | | | | | | Epsilon: 1.0328 | |==========================================================================================================================================================| | Iter | Active | Eval | log(1+valLoss)| Time for training | Observed min | Estimated min | Learner | Hyperparameter: Value | | | workers | result | | & validation (sec)| validation loss | validation loss | | | |==========================================================================================================================================================| | 81 | 7 | Accept | 2.9388 | 7.0653 | 2.8788 | 2.8778 | ensemble | Method: LSBoost | | | | | | | | | | NumLearningCycles: 375 | | | | | | | | | | MinLeafSize: 3 | | 82 | 4 | Accept | 2.9194 | 0.056852 | 2.8788 | 2.8778 | svm | BoxConstraint: 0.49279 | | | | | | | | | | KernelScale: 1.837 | | | | | | | | | | Epsilon: 0.028024 | | 83 | 4 | Accept | 3.6021 | 0.073288 | 2.8788 | 2.8778 | tree | MinLeafSize: 1 | | 84 | 4 | Accept | 4.1645 | 0.043986 | 2.8788 | 2.8778 | svm | BoxConstraint: 0.0010569 | | | | | | | | | | KernelScale: 0.05901 | | | | | | | | | | Epsilon: 154.61 | | 85 | 4 | Accept | 4.0662 | 0.051015 | 2.8788 | 2.8778 | svm | BoxConstraint: 0.65745 | | | | | | | | | | KernelScale: 42.989 | | | | | | | | | | Epsilon: 0.018275 | | 86 | 8 | Accept | 2.8973 | 2.9559 | 2.8788 | 2.8778 | ensemble | Method: Bag | | | | | | | | | | NumLearningCycles: 200 | | | | | | | | | | MinLeafSize: 21 | | 87 | 6 | Accept | 3.1593 | 0.030722 | 2.8788 | 2.8778 | tree | MinLeafSize: 8 | | 88 | 6 | Accept | 4.1645 | 0.1004 | 2.8788 | 2.8778 | svm | BoxConstraint: 0.026752 | | | | | | | | | | KernelScale: 0.0090205 | | | | | | | | | | Epsilon: 234.51 | | 89 | 6 | Accept | 4.1645 | 0.085556 | 2.8788 | 2.8778 | svm | BoxConstraint: 701.89 | | | | | | | | | | KernelScale: 0.014432 | | | | | | | | | | Epsilon: 823.78 | | 90 | 7 | Accept | 3.0786 | 0.058939 | 2.8788 | 2.8778 | tree | MinLeafSize: 12 |
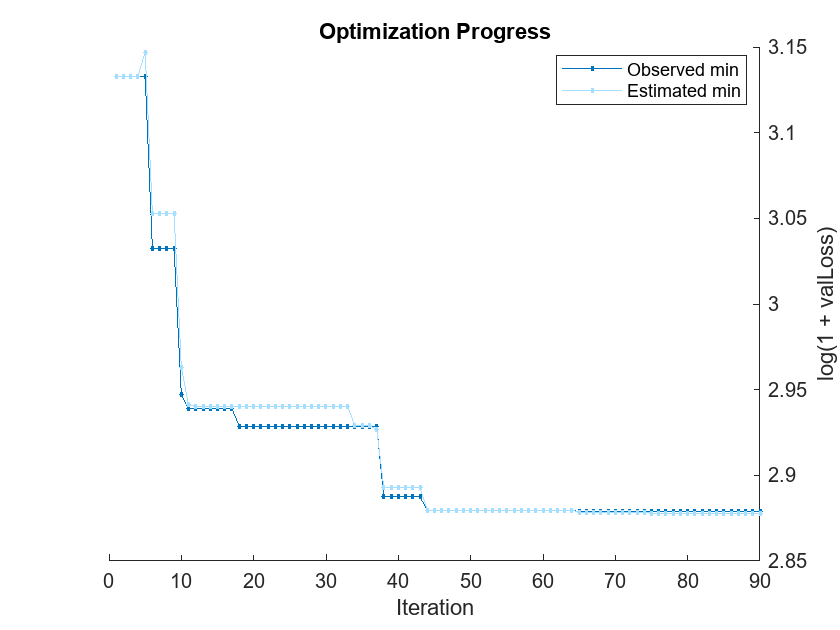
__________________________________________________________ Optimization completed. Total iterations: 90 Total elapsed time: 70.4919 seconds Total time for training and validation: 366.4178 seconds Best observed learner is an ensemble model with: Learner: ensemble Method: Bag NumLearningCycles: 223 MinLeafSize: 5 Observed log(1 + valLoss): 2.8788 Time for training and validation: 3.2047 seconds Best estimated learner (returned model) is an ensemble model with: Learner: ensemble Method: Bag NumLearningCycles: 223 MinLeafSize: 5 Estimated log(1 + valLoss): 2.8778 Estimated time for training and validation: 3.6185 seconds Documentation for fitrauto display
The final model returned by fitrauto corresponds to the best estimated learner. Before returning the model, the function retrains it using the entire training data (XTrain and YTrain), the listed Learner (or model) type, and the displayed hyperparameter values.
Evaluate Test Set Performance
Evaluate the performance of the model on the test set. testError is based on the test set mean squared error (MSE). Smaller MSE values indicate better performance.
testMSE = loss(Mdl,XTest,YTest); testError = log(1 + testMSE)
testError = 2.6223
Use fitrauto to automatically select a regression model with optimized hyperparameters, given predictor and response data stored in a table. Compare the performance of the resulting regression model to the performance of a simple linear regression model created with fitlm.
Load and Partition Data
Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Convert the Cylinders variable to a categorical variable. Create a table containing the predictor variables Acceleration, Cylinders, Displacement, and so on, as well as the response variable MPG.
load carbig Cylinders = categorical(Cylinders); cars = table(Acceleration,Cylinders,Displacement, ... Horsepower,Model_Year,Origin,Weight,MPG);
Delete rows of cars where the table has missing values.
cars = rmmissing(cars);
Categorize the cars based on whether they were made in the USA.
cars.Origin = categorical(cellstr(cars.Origin)); cars.Origin = mergecats(cars.Origin,["France","Japan",... "Germany","Sweden","Italy","England"],"NotUSA");
Partition the data into training and test sets. Use approximately 80% of the observations for training, and 20% of the observations for testing. Use cvpartition to partition the data.
rng("default") % For reproducibility of the data partition c = cvpartition(height(cars),"Holdout",0.2); trainingIdx = training(c); % Training set indices carsTrain = cars(trainingIdx,:); testIdx = test(c); % Test set indices carsTest = cars(testIdx,:);
Run fitrauto
Pass the training data to fitrauto. By default, fitrauto determines appropriate model types to try, uses Bayesian optimization to find good hyperparameter values, and returns a trained model autoMdl with the best expected performance. Specify to optimize over all optimizable hyperparameters and run the optimization in parallel (requires Parallel Computing Toolbox™).
Expect this process to take some time. By default, fitrauto provides a plot of the optimization and an iterative display of the optimization results. For more information on how to interpret these results, see Verbose Display.
options = struct("UseParallel",true); autoMdl = fitrauto(carsTrain,"MPG","OptimizeHyperparameters","all", ... "HyperparameterOptimizationOptions",options);
Starting parallel pool (parpool) using the 'Processes' profile ... Connected to parallel pool with 6 workers. Copying objective function to workers... Done copying objective function to workers. Learner types to explore: ensemble, svm, tree Total iterations (MaxObjectiveEvaluations): 90 Total time (MaxTime): Inf |==========================================================================================================================================================| | Iter | Active | Eval | log(1+valLoss)| Time for training | Observed min | Estimated min | Learner | Hyperparameter: Value | | | workers | result | | & validation (sec)| validation loss | validation loss | | | |==========================================================================================================================================================| | 1 | 6 | Best | 4.1303 | 3.4475 | 4.1303 | 4.1303 | svm | BoxConstraint: 0.0010671 | | | | | | | | | | KernelScale: 19.242 | | | | | | | | | | Epsilon: 44.847 | | 2 | 6 | Best | 3.1459 | 3.8766 | 3.1459 | 3.1459 | tree | MinLeafSize: 5 | | | | | | | | | | MaxNumSplits: 2 | | | | | | | | | | NumVariablesToSample: 3 | | 3 | 6 | Accept | 4.1303 | 1.4169 | 3.1459 | 3.1459 | svm | BoxConstraint: 0.73976 | | | | | | | | | | KernelScale: 2.7037 | | | | | | | | | | Epsilon: 38.421 | | 4 | 6 | Best | 2.5639 | 1.2712 | 2.5639 | 2.7048 | tree | MinLeafSize: 9 | | | | | | | | | | MaxNumSplits: 199 | | | | | | | | | | NumVariablesToSample: 5 | | 5 | 6 | Accept | 3.3002 | 0.33561 | 2.5639 | 2.564 | tree | MinLeafSize: 13 | | | | | | | | | | MaxNumSplits: 1 | | | | | | | | | | NumVariablesToSample: 4 | | 6 | 6 | Accept | 4.1303 | 0.21087 | 2.5639 | 2.564 | svm | BoxConstraint: 0.01028 | | | | | | | | | | KernelScale: 0.0032203 | | | | | | | | | | Epsilon: 36.299 | | 7 | 6 | Accept | 2.5852 | 0.41237 | 2.5639 | 2.564 | tree | MinLeafSize: 2 | | | | | | | | | | MaxNumSplits: 120 | | | | | | | | | | NumVariablesToSample: 7 | | 8 | 5 | Accept | 4.7998 | 13.852 | 2.5639 | 2.564 | ensemble | Method: LSBoost | | | | | | | | | | LearnRate: 0.0042702 | | | | | | | | | | MinLeafSize: 31 | | | | | | | | | | NumVariablesToSample: NaN | | 9 | 5 | Accept | 4.5891 | 11.084 | 2.5639 | 2.564 | ensemble | Method: LSBoost | | | | | | | | | | LearnRate: 0.0051188 | | | | | | | | | | MinLeafSize: 83 | | | | | | | | | | NumVariablesToSample: NaN | | 10 | 5 | Accept | 4.6825 | 11.581 | 2.5639 | 2.564 | ensemble | Method: LSBoost | | | | | | | | | | LearnRate: 0.0045559 | | | | | | | | | | MinLeafSize: 1 | | | | | | | | | | NumVariablesToSample: NaN | | 11 | 6 | Accept | 2.6585 | 0.63223 | 2.5639 | 2.5633 | tree | MinLeafSize: 5 | | | | | | | | | | MaxNumSplits: 61 | | | | | | | | | | NumVariablesToSample: 2 | | 12 | 6 | Accept | 2.5733 | 0.69096 | 2.5639 | 2.5653 | tree | MinLeafSize: 5 | | | | | | | | | | MaxNumSplits: 61 | | | | | | | | | | NumVariablesToSample: 2 | | 13 | 6 | Best | 2.2945 | 9.4664 | 2.2945 | 2.2956 | ensemble | Method: Bag | | | | | | | | | | LearnRate: NaN | | | | | | | | | | MinLeafSize: 2 | | | | | | | | | | NumVariablesToSample: 4 | | 14 | 6 | Accept | 4.1303 | 0.23153 | 2.2945 | 2.2956 | svm | BoxConstraint: 27.717 | | | | | | | | | | KernelScale: 21.172 | | | | | | | | | | Epsilon: 390.93 | | 15 | 6 | Accept | 2.6405 | 7.1727 | 2.2945 | 2.2988 | ensemble | Method: Bag | | | | | | | | | | LearnRate: NaN | | | | | | | | | | MinLeafSize: 45 | | | | | | | | | | NumVariablesToSample: 6 | | 16 | 5 | Accept | 2.3432 | 7.1757 | 2.2945 | 2.1873 | ensemble | Method: Bag | | | | | | | | | | LearnRate: NaN | | | | | | | | | | MinLeafSize: 1 | | | | | | | | | | NumVariablesToSample: 3 | | 17 | 5 | Accept | 2.8316 | 0.32852 | 2.2945 | 2.1873 | svm | BoxConstraint: 0.038615 | | | | | | | | | | KernelScale: 0.26266 | | | | | | | | | | Epsilon: 5.8807 | | 18 | 6 | Accept | 4.1551 | 6.261 | 2.2945 | 2.3249 | ensemble | Method: LSBoost | | | | | | | | | | LearnRate: 0.014547 | | | | | | | | | | MinLeafSize: 145 | | | | | | | | | | NumVariablesToSample: NaN | | 19 | 6 | Accept | 2.3708 | 7.183 | 2.2945 | 2.3532 | ensemble | Method: Bag | | | | | | | | | | LearnRate: NaN | | | | | | | | | | MinLeafSize: 26 | | | | | | | | | | NumVariablesToSample: 6 | | 20 | 6 | Accept | 2.5191 | 7.6483 | 2.2945 | 2.3519 | ensemble | Method: LSBoost | | | | | | | | | | LearnRate: 0.9913 | | | | | | | | | | MinLeafSize: 4 | | | | | | | | | | NumVariablesToSample: NaN | |==========================================================================================================================================================| | Iter | Active | Eval | log(1+valLoss)| Time for training | Observed min | Estimated min | Learner | Hyperparameter: Value | | | workers | result | | & validation (sec)| validation loss | validation loss | | | |==========================================================================================================================================================| | 21 | 5 | Accept | 2.5191 | 7.4956 | 2.2945 | 2.2937 | ensemble | Method: LSBoost | | | | | | | | | | LearnRate: 0.9913 | | | | | | | | | | MinLeafSize: 4 | | | | | | | | | | NumVariablesToSample: NaN | | 22 | 5 | Accept | 3.1622 | 7.0091 | 2.2945 | 2.2937 | ensemble | Method: Bag | | | | | | | | | | LearnRate: NaN | | | | | | | | | | MinLeafSize: 116 | | | | | | | | | | NumVariablesToSample: 6 | | 23 | 5 | Accept | 2.6846 | 0.2699 | 2.2945 | 2.2937 | tree | MinLeafSize: 1 | | | | | | | | | | MaxNumSplits: 248 | | | | | | | | | | NumVariablesToSample: 7 | | 24 | 5 | Accept | 3.0009 | 0.13263 | 2.2945 | 2.2937 | tree | MinLeafSize: 30 | | | | | | | | | | MaxNumSplits: 21 | | | | | | | | | | NumVariablesToSample: 2 | | 25 | 5 | Accept | 2.9014 | 0.056488 | 2.2945 | 2.2937 | tree | MinLeafSize: 2 | | | | | | | | | | MaxNumSplits: 4 | | | | | | | | | | NumVariablesToSample: 4 | | 26 | 6 | Accept | 2.5073 | 4.9712 | 2.2945 | 2.2937 | ensemble | Method: Bag | | | | | | | | | | LearnRate: NaN | | | | | | | | | | MinLeafSize: 29 | | | | | | | | | | NumVariablesToSample: 3 | | 27 | 6 | Accept | 2.4723 | 0.42317 | 2.2945 | 2.2937 | tree | MinLeafSize: 9 | | | | | | | | | | MaxNumSplits: 157 | | | | | | | | | | NumVariablesToSample: 6 | | 28 | 6 | Accept | 2.5015 | 4.7606 | 2.2945 | 2.294 | ensemble | Method: Bag | | | | | | | | | | LearnRate: NaN | | | | | | | | | | MinLeafSize: 11 | | | | | | | | | | NumVariablesToSample: 1 | | 29 | 6 | Accept | 2.499 | 5.0657 | 2.2945 | 2.294 | ensemble | Method: Bag | | | | | | | | | | LearnRate: NaN | | | | | | | | | | MinLeafSize: 11 | | | | | | | | | | NumVariablesToSample: 1 | | 30 | 6 | Accept | 4.1303 | 0.16935 | 2.2945 | 2.294 | svm | BoxConstraint: 0.0011506 | | | | | | | | | | KernelScale: 352.85 | | | | | | | | | | Epsilon: 163.49 | | 31 | 5 | Accept | 2.3265 | 6.3484 | 2.2945 | 2.294 | ensemble | Method: LSBoost | | | | | | | | | | LearnRate: 0.11482 | | | | | | | | | | MinLeafSize: 54 | | | | | | | | | | NumVariablesToSample: NaN | | 32 | 5 | Accept | 2.6676 | 0.14033 | 2.2945 | 2.294 | tree | MinLeafSize: 1 | | | | | | | | | | MaxNumSplits: 12 | | | | | | | | | | NumVariablesToSample: 4 | | 33 | 4 | Accept | 2.6931 | 1.5523 | 2.2945 | 2.294 | svm | BoxConstraint: 8.3226 | | | | | | | | | | KernelScale: 22.717 | | | | | | | | | | Epsilon: 3.2417 | | 34 | 4 | Accept | 3.3292 | 0.069533 | 2.2945 | 2.294 | tree | MinLeafSize: 72 | | | | | | | | | | MaxNumSplits: 251 | | | | | | | | | | NumVariablesToSample: 2 | | 35 | 4 | Accept | 2.7867 | 0.070147 | 2.2945 | 2.294 | tree | MinLeafSize: 4 | | | | | | | | | | MaxNumSplits: 5 | | | | | | | | | | NumVariablesToSample: 6 | | 36 | 4 | Accept | 4.1448 | 0.10004 | 2.2945 | 2.294 | svm | BoxConstraint: 1.8227 | | | | | | | | | | KernelScale: 977.3 | | | | | | | | | | Epsilon: 2.0809 | | 37 | 4 | Accept | 2.7305 | 0.071273 | 2.2945 | 2.294 | tree | MinLeafSize: 1 | | | | | | | | | | MaxNumSplits: 31 | | | | | | | | | | NumVariablesToSample: 4 | | 38 | 6 | Best | 2.1806 | 0.33042 | 2.1806 | 2.1808 | svm | BoxConstraint: 197.52 | | | | | | | | | | KernelScale: 4.7757 | | | | | | | | | | Epsilon: 0.029282 | | 39 | 6 | Accept | 2.1806 | 0.29825 | 2.1806 | 2.1807 | svm | BoxConstraint: 197.52 | | | | | | | | | | KernelScale: 4.7757 | | | | | | | | | | Epsilon: 0.029282 | | 40 | 5 | Accept | 2.1806 | 1.1365 | 2.1806 | 2.1807 | svm | BoxConstraint: 197.52 | | | | | | | | | | KernelScale: 4.7757 | | | | | | | | | | Epsilon: 0.029282 | |==========================================================================================================================================================| | Iter | Active | Eval | log(1+valLoss)| Time for training | Observed min | Estimated min | Learner | Hyperparameter: Value | | | workers | result | | & validation (sec)| validation loss | validation loss | | | |==========================================================================================================================================================| | 41 | 5 | Accept | 2.5404 | 0.11739 | 2.1806 | 2.1807 | tree | MinLeafSize: 2 | | | | | | | | | | MaxNumSplits: 257 | | | | | | | | | | NumVariablesToSample: 4 | | 42 | 6 | Accept | 2.7214 | 0.12168 | 2.1806 | 2.1807 | tree | MinLeafSize: 13 | | | | | | | | | | MaxNumSplits: 167 | | | | | | | | | | NumVariablesToSample: 3 | | 43 | 6 | Accept | 2.5848 | 0.060058 | 2.1806 | 2.1807 | tree | MinLeafSize: 17 | | | | | | | | | | MaxNumSplits: 12 | | | | | | | | | | NumVariablesToSample: 6 | | 44 | 6 | Best | 2.1759 | 0.11488 | 2.1759 | 2.1759 | svm | BoxConstraint: 0.19712 | | | | | | | | | | KernelScale: 2.8803 | | | | | | | | | | Epsilon: 0.07079 | | 45 | 6 | Accept | 4.1303 | 0.099786 | 2.1759 | 2.1758 | svm | BoxConstraint: 216.26 | | | | | | | | | | KernelScale: 0.0026892 | | | | | | | | | | Epsilon: 19.364 | | 46 | 6 | Accept | 3.2037 | 5.4636 | 2.1759 | 2.1758 | ensemble | Method: LSBoost | | | | | | | | | | LearnRate: 0.96271 | | | | | | | | | | MinLeafSize: 116 | | | | | | | | | | NumVariablesToSample: NaN | | 47 | 6 | Accept | 4.1303 | 0.10162 | 2.1759 | 2.1759 | svm | BoxConstraint: 0.0026925 | | | | | | | | | | KernelScale: 7.0869 | | | | | | | | | | Epsilon: 24.319 | | 48 | 6 | Accept | 2.3346 | 6.1175 | 2.1759 | 2.1759 | ensemble | Method: Bag | | | | | | | | | | LearnRate: NaN | | | | | | | | | | MinLeafSize: 22 | | | | | | | | | | NumVariablesToSample: 6 | | 49 | 6 | Accept | 3.1417 | 0.056998 | 2.1759 | 2.1759 | tree | MinLeafSize: 17 | | | | | | | | | | MaxNumSplits: 5 | | | | | | | | | | NumVariablesToSample: 1 | | 50 | 6 | Accept | 2.2905 | 0.15188 | 2.1759 | 2.1763 | svm | BoxConstraint: 0.43806 | | | | | | | | | | KernelScale: 4.5798 | | | | | | | | | | Epsilon: 0.054809 | | 51 | 6 | Accept | 4.1303 | 0.060906 | 2.1759 | 2.1766 | svm | BoxConstraint: 0.0017279 | | | | | | | | | | KernelScale: 0.59584 | | | | | | | | | | Epsilon: 49.918 | | 52 | 6 | Accept | 2.2872 | 5.7381 | 2.1759 | 2.1766 | ensemble | Method: Bag | | | | | | | | | | LearnRate: NaN | | | | | | | | | | MinLeafSize: 13 | | | | | | | | | | NumVariablesToSample: 4 | | 53 | 6 | Accept | 3.0447 | 0.074364 | 2.1759 | 2.1766 | tree | MinLeafSize: 45 | | | | | | | | | | MaxNumSplits: 13 | | | | | | | | | | NumVariablesToSample: 4 | | 54 | 6 | Accept | 4.1303 | 0.085215 | 2.1759 | 2.1766 | svm | BoxConstraint: 11.673 | | | | | | | | | | KernelScale: 0.43927 | | | | | | | | | | Epsilon: 22.967 | | 55 | 6 | Accept | 4.1303 | 0.09175 | 2.1759 | 2.1762 | svm | BoxConstraint: 2.5552 | | | | | | | | | | KernelScale: 0.0026113 | | | | | | | | | | Epsilon: 997.73 | | 56 | 6 | Accept | 4.1303 | 0.061439 | 2.1759 | 2.1768 | svm | BoxConstraint: 0.057299 | | | | | | | | | | KernelScale: 55.001 | | | | | | | | | | Epsilon: 715.72 | | 57 | 6 | Accept | 2.2057 | 6.0594 | 2.1759 | 2.1768 | ensemble | Method: LSBoost | | | | | | | | | | LearnRate: 0.22715 | | | | | | | | | | MinLeafSize: 5 | | | | | | | | | | NumVariablesToSample: NaN | | 58 | 6 | Accept | 2.1825 | 5.5939 | 2.1759 | 2.1768 | ensemble | Method: LSBoost | | | | | | | | | | LearnRate: 0.22153 | | | | | | | | | | MinLeafSize: 1 | | | | | | | | | | NumVariablesToSample: NaN | | 59 | 6 | Accept | 4.1303 | 0.071138 | 2.1759 | 2.1768 | tree | MinLeafSize: 132 | | | | | | | | | | MaxNumSplits: 17 | | | | | | | | | | NumVariablesToSample: 1 | | 60 | 6 | Accept | 4.1303 | 0.092724 | 2.1759 | 2.1763 | svm | BoxConstraint: 958.92 | | | | | | | | | | KernelScale: 0.70563 | | | | | | | | | | Epsilon: 537.94 | |==========================================================================================================================================================| | Iter | Active | Eval | log(1+valLoss)| Time for training | Observed min | Estimated min | Learner | Hyperparameter: Value | | | workers | result | | & validation (sec)| validation loss | validation loss | | | |==========================================================================================================================================================| | 61 | 5 | Accept | 5.2259 | 58.51 | 2.1759 | 2.1764 | svm | BoxConstraint: 0.95481 | | | | | | | | | | KernelScale: 0.0033698 | | | | | | | | | | Epsilon: 0.060804 | | 62 | 5 | Accept | 16.058 | 44.447 | 2.1759 | 2.1764 | svm | BoxConstraint: 0.87942 | | | | | | | | | | KernelScale: 0.042698 | | | | | | | | | | Epsilon: 4.1252 | | 63 | 5 | Accept | 2.8565 | 0.076866 | 2.1759 | 2.1764 | tree | MinLeafSize: 9 | | | | | | | | | | MaxNumSplits: 44 | | | | | | | | | | NumVariablesToSample: 2 | | 64 | 6 | Accept | 2.1905 | 6.0033 | 2.1759 | 2.1764 | ensemble | Method: LSBoost | | | | | | | | | | LearnRate: 0.086539 | | | | | | | | | | MinLeafSize: 1 | | | | | | | | | | NumVariablesToSample: NaN | | 65 | 6 | Accept | 4.1435 | 0.41502 | 2.1759 | 2.176 | svm | BoxConstraint: 0.0014713 | | | | | | | | | | KernelScale: 24.291 | | | | | | | | | | Epsilon: 0.0080531 | | 66 | 6 | Accept | 4.1303 | 0.06148 | 2.1759 | 2.176 | svm | BoxConstraint: 1004.8 | | | | | | | | | | KernelScale: 1.0362 | | | | | | | | | | Epsilon: 57.277 | | 67 | 6 | Accept | 2.2057 | 6.1759 | 2.1759 | 2.176 | ensemble | Method: LSBoost | | | | | | | | | | LearnRate: 0.065318 | | | | | | | | | | MinLeafSize: 1 | | | | | | | | | | NumVariablesToSample: NaN | | 68 | 6 | Accept | 2.6213 | 1.631 | 2.1759 | 2.176 | tree | MinLeafSize: 2 | | | | | | | | | | MaxNumSplits: 41 | | | | | | | | | | NumVariablesToSample: 5 | | 69 | 6 | Accept | 2.195 | 6.4848 | 2.1759 | 2.176 | ensemble | Method: LSBoost | | | | | | | | | | LearnRate: 0.064514 | | | | | | | | | | MinLeafSize: 1 | | | | | | | | | | NumVariablesToSample: NaN | | 70 | 5 | Best | 2.1681 | 5.6457 | 2.1681 | 2.1644 | ensemble | Method: LSBoost | | | | | | | | | | LearnRate: 0.1184 | | | | | | | | | | MinLeafSize: 4 | | | | | | | | | | NumVariablesToSample: NaN | | 71 | 5 | Accept | 2.1814 | 0.33738 | 2.1681 | 2.1644 | svm | BoxConstraint: 1066.5 | | | | | | | | | | KernelScale: 21.451 | | | | | | | | | | Epsilon: 1.5466 | | 72 | 6 | Accept | 6.622 | 32.752 | 2.1681 | 2.1644 | svm | BoxConstraint: 154.74 | | | | | | | | | | KernelScale: 0.43817 | | | | | | | | | | Epsilon: 0.069304 | | 73 | 6 | Accept | 2.1846 | 5.7951 | 2.1681 | 2.1682 | ensemble | Method: LSBoost | | | | | | | | | | LearnRate: 0.10013 | | | | | | | | | | MinLeafSize: 6 | | | | | | | | | | NumVariablesToSample: NaN | | 74 | 6 | Best | 2.1674 | 5.5415 | 2.1674 | 2.1681 | ensemble | Method: LSBoost | | | | | | | | | | LearnRate: 0.095942 | | | | | | | | | | MinLeafSize: 6 | | | | | | | | | | NumVariablesToSample: NaN | | 75 | 6 | Accept | 2.2257 | 5.8925 | 2.1674 | 2.1657 | ensemble | Method: LSBoost | | | | | | | | | | LearnRate: 0.082236 | | | | | | | | | | MinLeafSize: 7 | | | | | | | | | | NumVariablesToSample: NaN | | 76 | 6 | Accept | 2.6476 | 0.17979 | 2.1674 | 2.1657 | tree | MinLeafSize: 28 | | | | | | | | | | MaxNumSplits: 129 | | | | | | | | | | NumVariablesToSample: 7 | | 77 | 6 | Accept | 4.1303 | 0.20025 | 2.1674 | 2.1657 | svm | BoxConstraint: 88.122 | | | | | | | | | | KernelScale: 0.00080559 | | | | | | | | | | Epsilon: 80.763 | | 78 | 6 | Accept | 2.4686 | 0.08985 | 2.1674 | 2.1657 | tree | MinLeafSize: 11 | | | | | | | | | | MaxNumSplits: 185 | | | | | | | | | | NumVariablesToSample: 6 | | 79 | 6 | Accept | 6.0666 | 8.1575 | 2.1674 | 2.1655 | ensemble | Method: LSBoost | | | | | | | | | | LearnRate: 0.00091284 | | | | | | | | | | MinLeafSize: 1 | | | | | | | | | | NumVariablesToSample: NaN | | 80 | 6 | Accept | 3.2165 | 0.056294 | 2.1674 | 2.1655 | tree | MinLeafSize: 14 | | | | | | | | | | MaxNumSplits: 6 | | | | | | | | | | NumVariablesToSample: 1 | |==========================================================================================================================================================| | Iter | Active | Eval | log(1+valLoss)| Time for training | Observed min | Estimated min | Learner | Hyperparameter: Value | | | workers | result | | & validation (sec)| validation loss | validation loss | | | |==========================================================================================================================================================| | 81 | 6 | Accept | 2.245 | 7.6163 | 2.1674 | 2.1655 | ensemble | Method: Bag | | | | | | | | | | LearnRate: NaN | | | | | | | | | | MinLeafSize: 1 | | | | | | | | | | NumVariablesToSample: 7 | | 82 | 6 | Accept | 3.0936 | 5.5248 | 2.1674 | 2.1687 | ensemble | Method: LSBoost | | | | | | | | | | LearnRate: 0.011017 | | | | | | | | | | MinLeafSize: 76 | | | | | | | | | | NumVariablesToSample: NaN | | 83 | 6 | Accept | 4.5354 | 11.561 | 2.1674 | 2.1687 | svm | BoxConstraint: 0.022073 | | | | | | | | | | KernelScale: 0.0034124 | | | | | | | | | | Epsilon: 2.9088 | | 84 | 6 | Accept | 3.0342 | 0.062138 | 2.1674 | 2.1687 | tree | MinLeafSize: 19 | | | | | | | | | | MaxNumSplits: 3 | | | | | | | | | | NumVariablesToSample: 5 | | 85 | 6 | Accept | 4.13 | 4.1837 | 2.1674 | 2.1673 | ensemble | Method: Bag | | | | | | | | | | LearnRate: NaN | | | | | | | | | | MinLeafSize: 174 | | | | | | | | | | NumVariablesToSample: 5 | | 86 | 5 | Accept | 2.8788 | 4.5181 | 2.1674 | 2.1673 | ensemble | Method: Bag | | | | | | | | | | LearnRate: NaN | | | | | | | | | | MinLeafSize: 63 | | | | | | | | | | NumVariablesToSample: 3 | | 87 | 5 | Accept | 3.2232 | 0.083182 | 2.1674 | 2.1673 | tree | MinLeafSize: 66 | | | | | | | | | | MaxNumSplits: 75 | | | | | | | | | | NumVariablesToSample: 4 | | 88 | 6 | Accept | 2.7458 | 0.062397 | 2.1674 | 2.1673 | tree | MinLeafSize: 27 | | | | | | | | | | MaxNumSplits: 9 | | | | | | | | | | NumVariablesToSample: 5 | | 89 | 6 | Accept | 4.1483 | 0.084711 | 2.1674 | 2.1673 | svm | BoxConstraint: 0.10441 | | | | | | | | | | KernelScale: 1191.6 | | | | | | | | | | Epsilon: 0.80681 | | 90 | 6 | Accept | 2.5444 | 0.063012 | 2.1674 | 2.1673 | tree | MinLeafSize: 17 | | | | | | | | | | MaxNumSplits: 81 | | | | | | | | | | NumVariablesToSample: 6 |
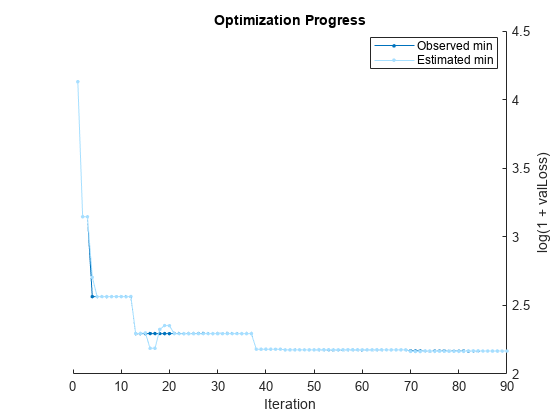
__________________________________________________________ Optimization completed. Total iterations: 90 Total elapsed time: 94.9921 seconds Total time for training and validation: 387.2946 seconds Best observed learner is an ensemble model with: Learner: ensemble Method: LSBoost LearnRate: 0.095942 MinLeafSize: 6 NumVariablesToSample: NaN Observed log(1 + valLoss): 2.1674 Time for training and validation: 5.5415 seconds Best estimated learner (returned model) is an ensemble model with: Learner: ensemble Method: LSBoost LearnRate: 0.1184 MinLeafSize: 4 NumVariablesToSample: NaN Estimated log(1 + valLoss): 2.1673 Estimated time for training and validation: 5.6503 seconds Documentation for fitrauto display
The final model returned by fitrauto corresponds to the best estimated learner. Before returning the model, the function retrains it using the entire training data (carsTrain), the listed Learner (or model) type, and the displayed hyperparameter values.
Create Simple Model
Create a simple linear regression model linearMdl by using the fitlm function.
linearMdl = fitlm(carsTrain);
Although the linearMdl object does not have the exact same properties and methods as the autoMdl object, you can use both models to predict response values for new data by using the predict object function.
Compare Test Set Performance of Models
Compare the performance of the linearMdl and autoMdl models on the test data set. For each model, compute the test set mean squared error (MSE). Smaller MSE values indicate better performance.
ypred = predict(linearMdl,carsTest);
linearMSE = mean((carsTest.MPG-ypred).^2,"omitnan")linearMSE = 10.0558
autoMSE = loss(autoMdl,carsTest,"MPG")autoMSE = 6.9868
The autoMdl model seems to outperform the linearMdl model.
Input Arguments
Sample data, specified as a table. Each row of Tbl corresponds to one observation, and each column corresponds to one predictor. Optionally, Tbl can contain one additional column for the response variable. Multicolumn variables and cell arrays other than cell arrays of character vectors are not accepted.
If Tbl contains the response variable, and you want to use all remaining
variables in Tbl as predictors, specify the response variable using
ResponseVarName.
If Tbl contains the response variable, and you want to use only a subset of the remaining variables in Tbl as predictors, specify a formula using formula.
If Tbl does not contain the response variable, specify a response variable using Y. The length of the response variable and the number of rows in Tbl must be equal.
Data Types: table
Response variable name, specified as the name of a variable in
Tbl. The response variable must be a numeric vector.
You must specify ResponseVarName as a character vector or string
scalar. For example, if the response variable Y is stored as
Tbl.Y, then specify it as "Y". Otherwise, the
software treats all columns of Tbl, including Y,
as predictors when training a model.
Data Types: char | string
Explanatory model of the response variable and a subset of the predictor variables,
specified as a character vector or string scalar in the form
"Y~x1+x2+x3". In this form, Y represents the
response variable, and x1, x2, and
x3 represent the predictor variables.
To specify a subset of variables in Tbl as predictors for
training the model, use a formula. If you specify a formula, then the software does not
use any variables in Tbl that do not appear in
formula.
The variable names in the formula must be both variable names in Tbl
(Tbl.Properties.VariableNames) and valid MATLAB® identifiers. You can verify the variable names in Tbl by
using the isvarname function. If the variable names
are not valid, then you can convert them by using the matlab.lang.makeValidName function.
Data Types: char | string
Response data, specified as a numeric vector. The length of Y
must be equal to the number of rows in Tbl or
X.
To specify the response variable name, use the ResponseName
name-value argument.
Data Types: single | double
Predictor data, specified as a numeric matrix.
Each row of X corresponds to one observation, and each column corresponds to one predictor.
The length of Y and the number of rows in X must be equal.
To specify the names of the predictors in the order of their appearance in
X, use the PredictorNames name-value
argument.
Data Types: single | double
Note
The software treats NaN, empty character vector
(''), empty string (""),
<missing>, and <undefined> elements as
missing data. The software removes rows of data corresponding to missing values in the
response variable. However, the treatment of missing values in the predictor data
X or Tbl varies among models (or
learners).
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: "HyperparameterOptimizationOptions",struct("MaxObjectiveEvaluations",200,"Verbose",2)
specifies to run 200 iterations of the optimization process (that is, try 200 model
hyperparameter combinations), and to display information in the Command Window about the
next model hyperparameter combination to be evaluated.
Optimizer Options
Types of regression models to try during the optimization, specified as a value in the first table below or one or more learner names in the second table. Specify multiple learner names as a string or cell array.
| Value | Description |
|---|---|
"auto" |
Note To provide the best hyperparameter optimization experience, the automatic selection of learners behavior is subject to frequent changes. For a more consistent selection of learners across software releases, explicitly specify the models you want to include. |
"all" | fitrauto selects all possible learners. |
"all-linear" | fitrauto selects linear
("linear") learners. |
"all-nonlinear" | fitrauto selects all nonlinear learners:
"ensemble", "gp",
"kernel", "net",
"svm" (with a Gaussian or polynomial kernel), and
"tree". |
Note
For greater efficiency, fitrauto does not select the following combinations of models when you specify one of the previous values.
"kernel"and"svm"(with a Gaussian kernel) —fitrautochooses the first when the predictor data has more than 11,000 observations, and the second otherwise."linear"and"svm"(with a linear kernel) —fitrautochooses the first.
| Learner Name | Description |
|---|---|
"ensemble" | Ensemble regression model |
"gp" | Gaussian process regression model |
"kernel" | Kernel regression model |
"linear" | Linear regression model for high-dimensional data |
"net" | Neural network regression model |
"svm" | Support vector machine regression model |
"tree" | Binary decision regression tree |
Example: "Learners","all"
Example: "Learners","ensemble"
Example: "Learners",["gp","svm"]
Hyperparameters to optimize, specified as "auto" or
"all". The optimizable hyperparameters depend on the model (or
learner), as described in this table.
| Learner Name | Hyperparameters for "auto" | Additional Hyperparameters for "all" | Notes |
|---|---|---|---|
"ensemble" | Method, NumLearningCycles, LearnRate, MinLeafSize | MaxNumSplits,
NumVariablesToSample | When the ensemble For more information, including
hyperparameter search ranges, see |
"gp" | Sigma, Standardize | BasisFunction, KernelFunction, KernelScale (KernelParameters) |
For more information, including hyperparameter search
ranges, see |
"kernel" | Epsilon, KernelScale, Lambda, Standardize | Learner, NumExpansionDimensions | For more information, including hyperparameter search ranges, see
OptimizeHyperparameters. Note that you cannot change
hyperparameter search ranges when you use
fitrauto. |
"linear" | Lambda, Learner | Regularization | For more information, including hyperparameter search ranges, see
OptimizeHyperparameters. Note that you cannot change
hyperparameter search ranges when you use
fitrauto. |
"net" | Activations, Lambda, LayerSizes, Standardize | LayerBiasesInitializer, LayerWeightsInitializer | For more information, including hyperparameter search ranges, see
OptimizeHyperparameters. Note that you cannot change
hyperparameter search ranges when you use
fitrauto. |
"svm" | BoxConstraint,
Epsilon, KernelScale,
Standardize | KernelFunction,
PolynomialOrder | When the For more information, including hyperparameter search
ranges, see |
"tree" | MinLeafSize | MaxNumSplits | For more information, including hyperparameter search ranges, see
OptimizeHyperparameters. Note that you cannot change
hyperparameter search ranges when you use
fitrauto. |
Note
When Learners is set to a value other than
"auto", the default values for the model hyperparameters not
being optimized match the default fit function values, unless otherwise indicated in
the table notes. When Learners is set to
"auto", the optimized hyperparameter search ranges and
nonoptimized hyperparameter values can vary, depending on the characteristics of the
training data. For more information, see Automatic Selection of Learners.
Example: "OptimizeHyperparameters","all"
Options for optimization, specified as a HyperparameterOptimizationOptions object or a structure. All the options
are optional. The options that you can set in a structure are the same as those in the
HyperparameterOptimizationOptions object.
| Option | Values | Default |
|---|---|---|
Optimizer |
| "bayesopt" |
ConstraintBounds | Constraint bounds for N optimization problems,
specified as an N-by-2 numeric matrix or
| [] |
ConstraintTarget | Constraint target for the optimization problems, specified as
| If you specify ConstraintBounds and
ConstraintType, then the default value is
"matlab". Otherwise, the default value is
[]. |
ConstraintType | Constraint type for the optimization problems, specified as
| [] |
MaxObjectiveEvaluations | Maximum number of objective function evaluations. If you specify multiple
optimization problems using ConstraintBounds, the value
of MaxObjectiveEvaluations applies to each optimization
problem individually. |
|
MaxTime | Time limit for the optimization, specified as a nonnegative real
scalar. The time limit is in seconds, as measured by | Inf |
ShowPlots | Logical value indicating whether to show plots of the optimization
progress. If this option is true, the software plots the
observed minimum validation loss against the iteration number. When you use
Bayesian optimization, the plot also shows the estimated minimum validation
loss. | true |
SaveIntermediateResults | Logical value indicating whether to save the optimization results. If
this option is true, the software overwrites a workspace
variable at each iteration. The variable is a BayesianOptimization object named
BayesoptResults if you use Bayesian optimization, and a
table named ASHAResults if you use ASHA optimization. If
you specify multiple optimization problems using
ConstraintBounds, the workspace variable is an AggregateBayesianOptimization object named
"AggregateBayesoptResults". | false |
Verbose | Display level at the command line:
| 1 |
UseParallel | Logical value indicating whether to run the optimization in parallel, which requires Parallel Computing Toolbox™. Due to the nonreproducibility of parallel timing, parallel optimization does not necessarily yield reproducible results. | false |
Repartition | Logical value indicating whether to repartition the
cross-validation at every iteration. If this option is
A value of | false |
MaxTrainingSetSize | Maximum number of observations in each training set for ASHA optimization, specified as a positive integer. This value matches the largest training set size. Note If you want to specify this value, the | Largest available training partition size
|
MinTrainingSetSize | Minimum number of observations in each training set for ASHA optimization, specified as a positive integer. This value is the lower bound for the smallest training set size. Note If you want to specify this value, the | 100 |
| Specify only one of the following three options. | ||
CVPartition | cvpartition object created by cvpartition | Kfold=5 if you do not specify a
cross-validation option |
Holdout | Scalar in the range (0,1) representing the holdout
fraction | |
Kfold | Integer greater than 1 | |
Example: HyperparameterOptimizationOptions=struct(UseParallel=true)
Data Types: struct | HyperparameterOptimizationOptions object
Regression Options
Categorical predictors list, specified as one of the values in this table.
| Value | Description |
|---|---|
| Vector of positive integers |
Each entry in the vector is an index value indicating that the corresponding predictor is
categorical. The index values are between 1 and If |
| Logical vector |
A |
| Character matrix | Each row of the matrix is the name of a predictor variable. The names must match the entries in PredictorNames. Pad the names with extra blanks so each row of the character matrix has the same length. |
| String array or cell array of character vectors | Each element in the array is the name of a predictor variable. The names must match the entries in PredictorNames. |
"all" | All predictors are categorical. |
By default, if the predictor data is in a table (Tbl),
fitrauto assumes that a variable is categorical if it is a
logical vector, categorical vector, character array, string array, or cell array of
character vectors. However, learners that use decision trees assume that
mathematically ordered categorical vectors are continuous variables. If the predictor
data is a matrix (X), fitrauto assumes
that all predictors are continuous. To identify any other predictors as categorical
predictors, specify them by using the CategoricalPredictors
name-value argument.
For more information on how fitting functions treat categorical predictors, see Automatic Creation of Dummy Variables.
Example: "CategoricalPredictors","all"
Data Types: single | double | logical | char | string | cell
Predictor variable names, specified as a string array of unique names or cell array of unique
character vectors. The functionality of PredictorNames depends on the
way you supply the training data.
If you supply
XandY, then you can usePredictorNamesto assign names to the predictor variables inX.The order of the names in
PredictorNamesmust correspond to the column order ofX. That is,PredictorNames{1}is the name ofX(:,1),PredictorNames{2}is the name ofX(:,2), and so on. Also,size(X,2)andnumel(PredictorNames)must be equal.By default,
PredictorNamesis{'x1','x2',...}.
If you supply
Tbl, then you can usePredictorNamesto choose which predictor variables to use in training. That is,fitrautouses only the predictor variables inPredictorNamesand the response variable during training.PredictorNamesmust be a subset ofTbl.Properties.VariableNamesand cannot include the name of the response variable.By default,
PredictorNamescontains the names of all predictor variables.A good practice is to specify the predictors for training using either
PredictorNamesorformula, but not both.
Example: "PredictorNames",["SepalLength","SepalWidth","PetalLength","PetalWidth"]
Data Types: string | cell
Response variable name, specified as a character vector or string scalar.
If you supply
Y, then you can useResponseNameto specify a name for the response variable.If you supply
ResponseVarNameorformula, then you cannot useResponseName.
Example: ResponseName="response"
Data Types: char | string
Observation weights, specified as a positive numeric vector or the name of a
variable in Tbl. The software weights each observation in
X or Tbl with the corresponding value in
Weights. The length of Weights must equal
the number of rows in X or Tbl.
If you specify the input data as a table Tbl, then
Weights can be the name of a variable in
Tbl that contains a numeric vector. In this case, you must
specify Weights as a character vector or string scalar. For
example, if the weights vector W is stored as
Tbl.W, then specify it as "W". Otherwise, the
software treats all columns of Tbl, including
W, as predictors or the response variable when training the
model.
fitrauto ignores observation weights for Gaussian process
regression models. That is, when Learners includes
"gp" models, the function ignores the Weights
name-value argument for those models.
By default, Weights is ones(n,1), where
n is the number of observations in X or
Tbl.
The software normalizes Weights to sum to 1. Inf weights are not supported.
Data Types: single | double | char | string
Output Arguments
Trained regression model, returned as one of the regression model objects in the
following table. If you specify OptimizeHyperparameters and
set the ConstraintType and ConstraintBounds options of
HyperparameterOptimizationOptions, then Mdl is an
N-by-1 cell array of model objects, where N is equal
to the number of rows in ConstraintBounds. If none of the optimization
problems yields a feasible model, then each cell array value is [].
| Learner Name | Returned Model Object |
|---|---|
"ensemble" | CompactRegressionEnsemble |
"gp" | CompactRegressionGP |
"kernel" | RegressionKernel |
"linear" | RegressionLinear |
"net" | CompactRegressionNeuralNetwork |
"svm" | CompactRegressionSVM |
"tree" | CompactRegressionTree |
Optimization results, returned as a BayesianOptimization object, an AggregateBayesianOptimization object, or a table. If you set the
ConstraintType and ConstraintBounds options
of HyperparameterOptimizationOptions, then
OptimizationResults is an
AggregateBayesianOptimization object. If you do not set
ConstraintType and ConstraintBounds, then
OptimizationResults is a BayesianOptimization
object if Optimizer is 'bayesopt', or a table if
Optimizer is 'asha'. For more information, see
Bayesian Optimization and ASHA Optimization.
More About
When you set the Verbose field of the
HyperparameterOptimizationOptions name-value argument to
1 or 2, the fitrauto function
provides an iterative display of the optimization results.
The following table describes the columns in the display and their entries.
| Column Name | Description |
|---|---|
Iter | Iteration number — You can set a limit to the number of iterations by using
the MaxObjectiveEvaluations field of the
HyperparameterOptimizationOptions name-value
argument. |
Active workers | Number of active parallel workers — This column appears only when you run the
optimization in parallel by setting the UseParallel field of
the HyperparameterOptimizationOptions name-value argument to
true. |
Eval result | One of the following evaluation results:
|
log(1 + valLoss) | Log-transformed validation loss computed for the learner and hyperparameter
values at this iteration — In particular, fitrauto computes log(1 + valLoss), where valLoss is the cross-validation mean
squared error (MSE) by default. You can change the validation scheme by using the
CVPartition, Holdout, or
Kfold field of the
'HyperparameterOptimizationOptions' name-value
argument. |
Time for training & validation (sec) | Time taken to train and compute the validation loss for the model with the learner and hyperparameter values at this iteration (in seconds) — When you use Bayesian optimization, this value excludes the time required to update the objective function model maintained by the Bayesian optimization process. For more details, see Bayesian Optimization. |
Observed min log(1 + valLoss) | Observed minimum log-transformed validation loss computed so far — This
value corresponds to the smallest By default,
|
Estimated min log(1 + valLoss) | Estimated minimum log-transformed validation loss — When you use
Bayesian optimization, By default, Note This column appears only when you use Bayesian optimization, that is, when
the |
Training set size | Number of observations used in each training set at this iteration —
Use the Note This column appears only when you use ASHA optimization, that is, when the
|
Constraint1 violation | Amount by which the constraint bounds are violated. A nonpositive value
indicates that the value of the constraint is within the constraint bounds. This
column is displayed if you set the ConstraintType and
ConstraintBounds options of HyperparameterOptimizationOptions . |
Learner | Model type evaluated at this iteration — Specify the learners used in the
optimization by using the Learners name-value
argument. |
Hyperparameter: Value | Hyperparameter values at this iteration — Specify the hyperparameters used in
the optimization by using the OptimizeHyperparameters
name-value argument. |
The display also includes these model descriptions:
Best observed learner— This model, with the listed learner type and hyperparameter values, yields the final observed minimum validation loss (log-transformed). (For more information, see the description forObserved min log(1 + valLoss)in the previous table.) When you use ASHA optimization,fitrautoretrains the model on the entire training data set and returns it as theMdloutput.Best estimated learner— This model, with the listed learner type and hyperparameter values, yields the final estimated minimum validation loss (log-transformed) when you use Bayesian optimization. (For more information, see the description forEstimated min log(1 + valLoss)in the previous table.) In this case,fitrautoretrains the model on the entire training data set and returns it as theMdloutput.Note
The
Best estimated learnermodel appears only when you use Bayesian optimization, that is, when theOptimizerfield of theHyperparameterOptimizationOptionsname-value argument is set to"bayesopt".
Tips
Depending on the size of your data set, the number of learners you specify, and the optimization method you choose,
fitrautocan take some time to run.If you have a Parallel Computing Toolbox license, you can speed up computations by running the optimization in parallel. To do so, specify
"HyperparameterOptimizationOptions",struct("UseParallel",true). You can include additional fields in the structure to control other aspects of the optimization. SeeHyperparameterOptimizationOptions.If
fitrautowith Bayesian optimization takes a long time to run because of the number of observations in your training set (for example, over 10,000), consider usingfitrautowith ASHA optimization instead. ASHA optimization often finds good solutions faster than Bayesian optimization for data sets with many observations. To use ASHA optimization, specify"HyperparameterOptimizationOptions",struct("Optimizer","asha"). You can include additional fields in the structure to control additional aspects of the optimization. In particular, if you have a time constraint, specify theMaxTimefield of theHyperparameterOptimizationOptionsstructure to limit the number of secondsfitrautoruns.
Algorithms
When you specify "Learners","auto", the fitrauto
function analyzes the predictor and response data in order to choose appropriate learners.
The function considers whether the data set has any of these characteristics:
Categorical predictors
Missing values for more than 5% of the data
Wide data, where the number of predictors is greater than or equal to the number of observations
High-dimensional data, where the number of predictors is greater than 100
Large data, where the number of observations is greater than 50,000
The selected learners are always a subset of those listed in the Learners table.
However, the associated models tried during the optimization process can have different
default values for hyperparameters not being optimized, as well as different search ranges
for hyperparameters being optimized.
The goal of Bayesian optimization, and optimization in general, is to find a point that
minimizes an objective function. In the context of fitrauto, a point is
a learner type together with a set of hyperparameter values for the learner (see Learners and
OptimizeHyperparameters), and the objective function is log(1 + valLoss), where valLoss is the cross-validation mean squared
error (MSE), by default. The Bayesian optimization implemented in
fitrauto internally maintains a multi-RegressionGP model of the objective function. That is, the objective function
model splits along the learner type and, for a given learner, the model is a Gaussian
process regression (GPR) model. (This underlying model differs from the single GPR model
employed by other Statistics and Machine Learning Toolbox™ functions that use Bayesian optimization.) Bayesian optimization trains the
underlying model by using objective function evaluations, and determines the next point to
evaluate by using an acquisition function ("expected-improvement"). For
more information, see Expected Improvement. The acquisition function balances between sampling at
points with low modeled objective function values and exploring areas that are not well
modeled yet. At the end of the optimization, fitrauto chooses the point
with the minimum objective function model value, among the points evaluated during the
optimization. For more information, see the
"Criterion","min-visited-mean" name-value argument of bestPoint.
The asynchronous successive halving algorithm (ASHA) in fitrauto
randomly chooses several models with different hyperparameter values (see Learners and
OptimizeHyperparameters) and trains them on a small subset of the training
data. If the performance of a particular model is promising, the model is promoted and
trained on a larger amount of the training data. This process repeats, and successful models
are trained on progressively larger amounts of data. By default, at the end of the
optimization, fitrauto chooses the model that has the lowest log(1 + valLoss) value, where valLoss is the cross-validation mean
squared error (MSE).
At each iteration, ASHA either chooses a previously trained model and promotes it (that is, retrains the model using more training data), or selects a new model (learner type and hyperparameter values) using random search. ASHA promotes models as follows:
The algorithm searches for the group of models with the largest training set size for which this condition does not hold:
floor(g/4)of the models have been promoted, wheregis the number of models in the group.Among the group of models, ASHA chooses the model with the lowest log(1 + valLoss) value and retrains that model with
4*(Training Set Size)observations.If no such group of models exists, then ASHA selects a new model instead of promoting an old one, and trains the new model using the smallest training set size.
When a model is trained on a subset of the training data, ASHA computes the cross-validation MSE in the as follows:
For each training fold, the algorithm selects a random sample of the observations (of size
Training set size) using nonstratified sampling, and then trains a model on that subset of data.The algorithm then tests the fitted model on the test fold (that is, the observations not in the training fold) and computes the MSE.
Finally, the algorithm averages the results across all folds.
For more information on ASHA, see [1].
When you use ASHA optimization, the default number of iterations depends on the number
of observations in the data, the number of learner types, the use of parallel processing,
and the type of cross-validation. The algorithm selects the number of iterations such that,
for L learner types (see Learners),
fitrauto trains L models on the largest training
set size.
This table describes the default number of iterations based on the given specifications when you use 5-fold cross-validation. Note that n represents the number of observations and L represents the number of learner types.
Number of Observations n | Default Number of Iterations (run in serial) | Default Number of Iterations (run in parallel) |
|---|---|---|
| n < 500 | 30*L — n is too small to implement ASHA
optimization, and fitrauto implements random search to find and
assess models instead. | 30*L — n is too small to implement ASHA
optimization, and fitrauto implements random search to find and
assess models instead. |
| 500 ≤ n < 2000 | 5*L | 5*(L + 1) |
| 2000 ≤ n < 8000 | 21*L | 21*(L + 1) |
| 8000 ≤ n < 32,000 | 85*L | 85*(L + 1) |
| 32,000 ≤ n | 341*L | 341*(L + 1) |
Alternative Functionality
If you are unsure which models work best for your data set, you can alternatively use the Regression Learner app. Using the app, you can perform hyperparameter tuning for different models, and choose the optimized model that performs best. Although you must select a specific model before you can tune the model hyperparameters, Regression Learner provides greater flexibility for selecting optimizable hyperparameters and setting hyperparameter values. The app also allows you to train a variety of linear regression models (see Linear Regression Models). However, you cannot optimize in parallel, specify observation weights, or use ASHA optimization in the app. For more information, see Hyperparameter Optimization in Regression Learner App.
If you know which models might suit your data, you can alternatively use the corresponding model fit functions and specify the
OptimizeHyperparametersname-value argument to tune hyperparameters. You can compare the results across the models to select the best regression model. For an example of this process applied to classification models, see Moving Towards Automating Model Selection Using Bayesian Optimization.
References
[1] Li, Liam, Kevin Jamieson, Afshin Rostamizadeh, Ekaterina Gonina, Moritz Hardt, Benjamin Recht, and Ameet Talwalkar. “A System for Massively Parallel Hyperparameter Tuning.” ArXiv:1810.05934v5 [Cs], March 16, 2020. https://arxiv.org/abs/1810.05934v5.
Extended Capabilities
To perform parallel hyperparameter optimization, use the
UseParallel=true option in the
HyperparameterOptimizationOptions name-value pair argument in the call
to the fitrauto function.
For more information on parallel hyperparameter optimization, see Parallel Bayesian Optimization.
For general information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
Version History
Introduced in R2020bfitrauto defaults to serial hyperparameter optimization when
HyperparameterOptimizationOptions includes
UseParallel=true and the software cannot open a parallel pool.
In previous releases, the software issues an error under these circumstances.
Starting in R2023b, when the Learners value includes Gaussian
process regression ("gp"), kernel ("kernel"), or
support vector machine ("svm") models, the
fitrauto function optimizes the Standardize
hyperparameter of the models by default. That is, if the
OptimizeHyperparameters value is "auto", then
Standardize is an optimizable hyperparameter of GPR, kernel, and SVM
models.
Starting in R2023b, fitrauto optimizes the kernel scale parameter for Gaussian process regression (GPR) models by using the default search range [1e-3,1e3]. That is, when you specify to optimize the GPR hyperparameter KernelScale by using the OptimizeHyperparameters name-value argument, the function searches among positive values log-scaled in the range [1e-3,1e3].
In previous releases, the default search range for the KernelScale hyperparameter was [1e-3*MaxPredictorRange,MaxPredictorRange], where MaxPredictorRange = max(max(X) - min(X)).
The fitrauto function includes ARD kernel options for Gaussian
process regression ("gp") learners when the
OptimizeHyperparameters value is "all" and the
data set has these characteristics:
The number of observations is less than or equal to 10,000.
The number of predictors is less than or equal to 32 after the expansion of the categorical predictors (see Automatic Creation of Dummy Variables).
When the KernelFunction value of a GPR model is an ARD kernel option,
fitrauto trains the model using these GPR tolerance and initial step
size values:
The
OptimizerOptionsvalue matches the followingoptionsstructure:options = statset("fitrgp"); options.MaxIter = 1000; options.TolFun = 1e-3; options.TolX = 1e-3;The
InitialStepSizevalue is"auto".
In previous releases, the fitrauto function ignored all ARD kernel
options for GPR learners, regardless of the size of the data set.
Starting in R2022a, the list of available learners includes neural network models. When you
specify "all" or "all-nonlinear" for the
Learners name-value argument, fitrauto
includes neural network models as part of the model selection and hyperparameter tuning
process. The function also considers neural network models when you specify
Learners as "auto", depending on the
characteristics of your data set.
To omit neural network models from the model selection process, you can explicitly specify the
models you want to include. For example, to use tree and ensemble models only, specify
"Learners",["tree","ensemble"].
Starting in R2022a, if you specify Learners as
"auto" and the data has more predictors than observations after the
expansion of the categorical predictors (see Automatic Creation of Dummy Variables), then
fitrauto includes linear learners ("linear")
along with other models during the hyperparameter optimization. In previous releases, linear
learners were not considered.
Starting in R2021a, when you specify to try a linear learner
("linear"), fitrauto uses either a
Limited-memory BFGS (LBFGS) solver or a Sparse Reconstruction by Separable Approximation
(SpaRSA) solver, depending on the regularization type selected during that iteration of the
optimization process.
When
Regularizationis'ridge', the function sets theSolvervalue to'lbfgs'by default.When
Regularizationis'lasso', the function sets theSolvervalue to'sparsa'by default.
In previous releases, the default solver selection during the optimization process
depended on various factors, including the regularization type, learner type, and number of
predictors. For more information, see Solver.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)